题目描述
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
示例1
输入
[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]
返回值
{1,2,5,3,4,6,7}
复习前序,中序,后序遍历
(1)前序遍历
a、访问根节点;b、前序遍历左子树;c、前序遍历右子树。(根左右,特点:根在第一个位置上)
(2)中序遍历
a、中序遍历左子树;b、访问根节点;c、中序遍历右子树。(左根右,特点:根在中间,分左右)
(3)后序遍历
a、后序遍历左子树;b、后续遍历右子树;c、访问根节点。(左右根,特点:根在最后)
已知上面任意两个遍历方式即可画出二叉树(不必是满二叉树),并且写出另外一种遍历方式
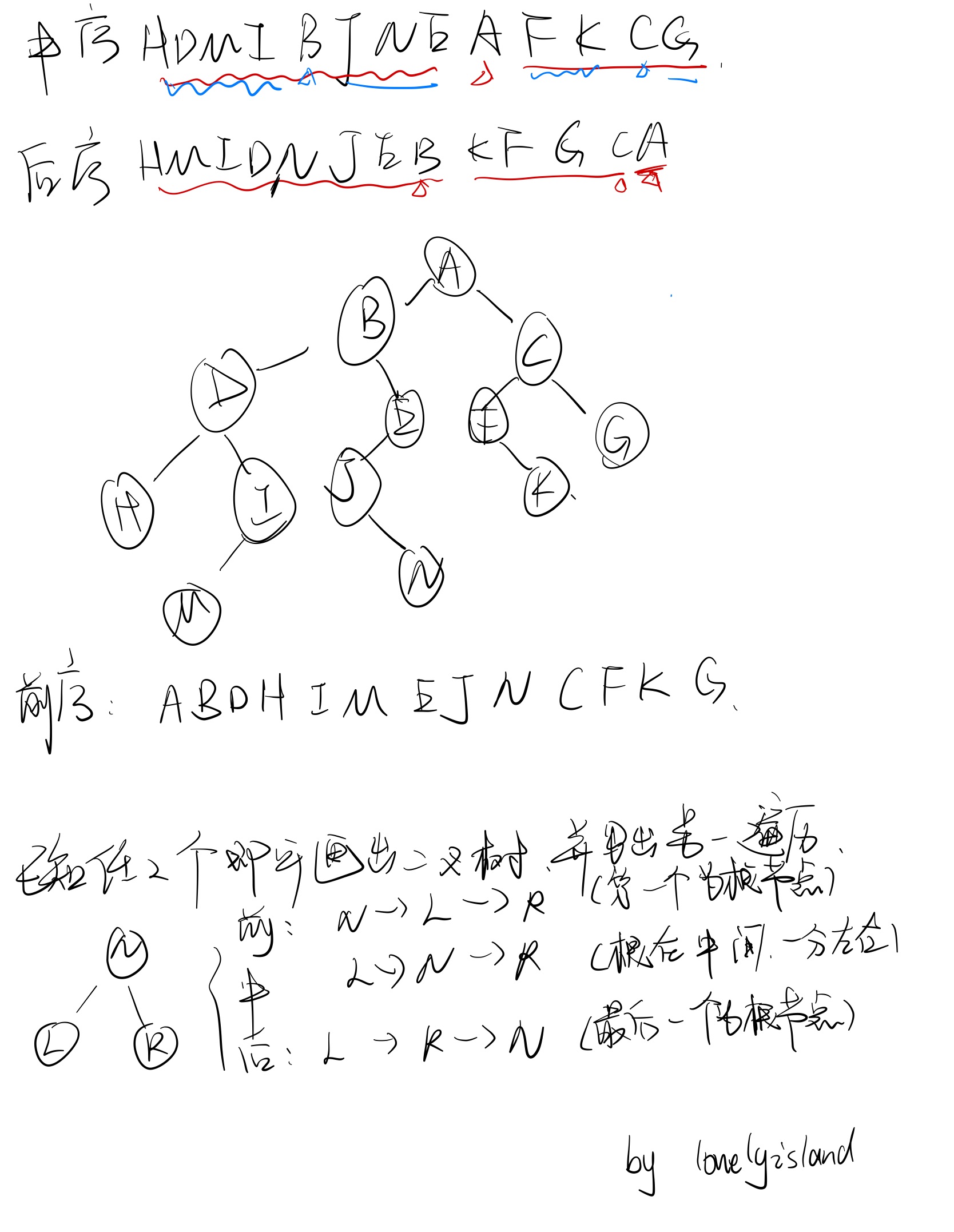
思路
已知前序遍历和中序遍历,我们重建的二叉树的时候便会使用这两种遍历方式的特点进行重建。首先确定根节点,即前序遍历的第一个元素。新建树的根节点后,在中序遍历中找到根节点位置,分开左右子树。在左右子树中进行上述步骤,即一个递归的过程。
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.Arrays;
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
if(pre.length==0 || in.length==0)
return null;
TreeNode root = new TreeNode(pre[0]);//使用前序遍历第一个节点作为根节点
for(int i = 0; i < in.length; i++){
if(in[i] == pre[0]){//查找到中序遍历中的根节点,分开左右子树
//左子树,copyOfRange函数左闭右开,递归的建立树结构
root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i+1), Arrays.copyOfRange(in, 0, i));
//类似,对右子树进行类似操作
root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i+1, pre.length), Arrays.copyOfRange(in, i + 1, in.length));
break;
}
}
return root;
}
}