emmm,验波题后。。。。我觉得各位萌新最多3题。。。because我就是个萌新啊!!
题目链接:http://acm.csust.edu.cn/contest/67
(这个比赛链接在比赛后无法提交的,所以要到题库里面去搜索一下就好了)
A.合并(思维题)
B.驯龙高手pph(BFS|DP)
C.echo的画家梦想I(树DP)
D.echo的画家梦想II(树DP)
E.厂里田径赛(树状数组|线段树)
emmm,相对来讲A,B,E题非常简单,2个小时是绰绰有余的,所以正常来讲各位萌新3题应该OK。至于CD两题。。。。确实不太友好
为了便于大家理解,有些题我会尝试一些乱七八糟的解法(可能会A,可能不会),可能会比较眼花缭乱,也不需要大家都掌握,不过某个出题人解法就一定要会了。
A.合并
题目大意:给你一个长度为n的序列,你可以将相邻的两个元素比如$i,i+1$合并,得到的利益为$a_{i}a_{i+1}$,合并之后的新元素为$a_{i}+a_{i+1}$。问你最多获得的利益为多少。
Sample Input
3 1 2 3
Sample Output
11
看起来似乎好像是个区间DP。。。但实际上我们手算一下就知道,这个合并的顺序是没有任何关系的。也就是说我们可以直接按顺序合并就OK了。
举个例子:这里有三个元素$a_{1},a_{2},a_{3}$我们看他的两种合并方式:
$(a_{1} imes a_{2})+a_{3}(a_{1}+a_{2})Rightarrow a_{1}a_{2}+a_{1}a_{3}+a_{2}a_{3}$
$a_{2}*a_{3}+a_{1}(a_{2}+a_{3})Rightarrow a_{1}a_{2}+a_{1}a_{3}+a_{2}a_{3}$
结果不言而喻,当然,这个结论也可以推广到n个元素的时候,就不多说了。任何用个前缀和维护一下前面加起来的值就好了
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=5e2+10; typedef long long ll; ll sum[mac]; int main() { int n; scanf ("%d",&n); ll ans=0; for (int i=1; i<=n; i++){ int x; scanf ("%d",&x); sum[i]=sum[i-1]+x; if (i==1) continue; ans+=sum[i-1]*x; } printf("%lld ",ans); return 0; }
B.驯龙高手pph
题目大意:给你初始坐标$(0,0),(0,1)$,这是龙王所处的位置,它现在想到坐标$(n-1,n-1),(n-1,n-2)$去,中间有些障碍。它有4种走法:
1.向右走;2.向下走;3.如果当前处于水平状态,且下面两格是空的,那么他可以顺时针旋转90度,从$(x,y),(x+1,y)Rightarrow (x,y),(x,y+1)$
4.如果当前处于垂直状态,且右边两格是空的,那么他可以逆时针旋转90度,从$(x,y),(x,y+1)Rightarrow (x,y),(x+1,y)$
Sample Input 1
6 0 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 0 0 0 1 1 0 0 0
Sample Output
11
emmmm,裸的BFS,首先我们可以想到模拟+BFS,即我们将这个占着2个格子的龙王用struct封装起来当做一个点来跑BFS就行了,我们在struct内部定义一下各种需要的方法就好了,比如说4种走法,到终点的判断等。关于判断状态是否经历过,我们可以直接使用类似Hash的方法,将每个格子化为$xy$值,然后用map嵌套pair保存一下两个格子的状态即可。
emmm...900ms+,代码跑得有点久,实际上是可以进行相当大的时间压缩的,只不过我懒得优化了。。。当然也有其他的优秀的做法,只不过这个是最为暴力和容易想到的
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=3e3+10; typedef long long ll; const int mod=4e3; int mp[mac][mac],mark=0,n; typedef pair<int,int>two; map<two,int>vis; struct node { int x1,y1,x2,y2; node(int x,int y,int x0,int y0){ x1=x;y1=y;x2=x0;y2=y0; } bool visted(){ int p1=x1*mod+y1;//化为xy int p2=x2*mod+y2; if (vis[make_pair(p1,p2)]) return true; vis[make_pair(p1,p2)]=1; vis[make_pair(p2,p1)]=1; return false; } bool final(){ if (x1==n && y1==n && x2==n && y2==n-1) return true; if (x2==n && y2==n && x1==n && y1==n-1) return true; return false; } bool right(){ int yy1=y1+1,yy2=y2+1; if (yy1>n || yy2>n || mp[x1][yy1] || mp[x2][yy2]) return false; y1=yy1;y2=yy2; return true; } bool down(){ int xx1=x1+1,xx2=x2+1; if (xx1>n || xx2>n || mp[xx1][y1] || mp[xx2][y2]) return false; x1=xx1;x2=xx2; return true; } int sta(){ if (y2==y1+1 || y1==y2+1) return 1;//水平状态 else return 2;//垂直状态 } bool clock(){//水平状态,顺时针转 if (mp[x1+1][y1] || mp[x2+1][y2] || x1+1>n || x2+1>n) return false; x2=x1+1;y2=y1; return true; } bool unclock(){//垂直状态,逆时针转 if (mp[x1][y1+1] || mp[x2][y2+1] || y1+1>n || y2+1>n) return false; x2=x1;y2=y1+1; return true; } }; struct moves { node drag; int time; }; void bfs(node st,int time,int n) { queue<moves>q; q.push(moves{st,0}); while (!q.empty()){ moves now=q.front(); q.pop(); node u=now.drag; node u_cp=u; if (u.visted()) continue; if (u.final()) { mark=1; printf("%d ",now.time); return; } if (u.right()) q.push(moves{u,now.time+1}),u=u_cp; if (u.down()) q.push(moves{u,now.time+1}),u=u_cp; int stk=u.sta(); if (stk==1){//水平状态顺时针转动 if (u.clock()) q.push(moves{u,now.time+1}),u=u_cp; } else { if (u.unclock()) q.push(moves{u,now.time+1}); } } } int main() { //freopen("in.txt","r",stdin); scanf ("%d",&n); for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) scanf("%d",&mp[i][j]); node star=node{1,1,1,2}; bfs(star,0,n); if (!mark) printf("-1 "); return 0; }
接下来我们不用模拟了,直接BFS,实际上这题我们可以看做一个点的移动,只不过这个点有两个状态,我们只要考虑把$(0,0)$移动到$(n-1,n-2)$就行了。然后用三维数组标记点0代表水平,1代表垂直状态。然后就是个裸的BFS了。。。
emmm,加了个快读,70ms+比上面的模拟+BFS快了不少
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=1e3+10; int mp[mac][mac],mark=0; bool vis[mac][mac][2];//0代表水平,1代表垂直 struct node { int x,y,t,stk;//坐标,时间,状态 }; void in(int &x) { int f=0; char ch=getchar(); while (ch>'9' || ch<'0') ch=getchar(); while (ch>='0' && ch<='9') f=(f<<3)+(f<<1)+ch-'0',ch=getchar(); x=f; } void bfs(node st,int n) { queue<node>q; q.push(st); while (!q.empty()){ node now=q.front(); q.pop(); int x=now.x,y=now.y; if (vis[x][y][now.stk]) continue; vis[x][y][now.stk]=true; //printf("%d %d %d %d ",now.x,now.y,now.t,now.stk); if (x==n && y==n-1 && !now.stk) {printf("%d ",now.t); mark=1; return;} if (!now.stk){//水平状态 if (!mp[x][y+2] && y+2<=n) q.push(node{x,y+1,now.t+1,now.stk});//右移 if (!mp[x+1][y] && !mp[x+1][y+1] && x+1<=n) { q.push(node{x+1,y,now.t+1,now.stk});//下移 q.push(node{x,y,now.t+1,now.stk^1});//顺时针旋转 } } else {//垂直状态 if (!mp[x][y+1] && !mp[x+1][y+1] && y+1<=n){ q.push(node{x,y+1,now.t+1,now.stk});//右移 q.push(node{x,y,now.t+1,now.stk^1});//逆时针旋转 } if (!mp[x+2][y] && x+2<=n) q.push(node{x+1,y,now.t+1,now.stk});//下移 } } } int main() { int n; in(n); for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) in(mp[i][j]); bfs(node{1,1,0,0},n); if (!mark) printf("-1 "); return 0; }
接下来就是DP解法(出题人解法),我们任然是考虑把$(0,0)$移动到$(n-1,n-2)$,然后建立状态转移方程,很明显这是个三维的dp,其转移方程应该不难写出,每一个点它要么是从上面转移过来的,要么是从左边转移过来的,然后观察一下周围的环境进行转移即可
emmm,40ms+,跑得最快的了。。。
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=1e3+10; int mp[mac][mac]; int dp[mac][mac][2];//0代表水平,1代表垂直 const int inf=1e8+10; void in(int &x) { int f=0; char ch=getchar(); while (ch>'9' || ch<'0') ch=getchar(); while (ch>='0' && ch<='9') f=(f<<3)+(f<<1)+ch-'0',ch=getchar(); x=f; } void solve(int n) { dp[1][1][0]=0; for (int i=1; i<=n; i++){ for (int j=1; j<=n; j++){ if (mp[i][j]) continue; //从上面转移过来的 if (!mp[i][j+1] && j+1<=n) dp[i][j][0]=min(dp[i][j][0],dp[i-1][j][0]+1); if (!mp[i+1][j] && i+1<=n) dp[i][j][1]=min(dp[i][j][1],dp[i-1][j][1]+1); //从左边转移过来的 if (!mp[i][j+1] && j+1<=n) dp[i][j][0]=min(dp[i][j][0],dp[i][j-1][0]+1); if (!mp[i+1][j] && i+1<=n) dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][1]+1); //变形, if (!mp[i+1][j] && !mp[i+1][j+1] && i+1<=n && j+1<=n) dp[i][j][1]=min(dp[i][j][1],dp[i][j][0]+1);//由水平到垂直 if (!mp[i][j+1] && !mp[i+1][j+1] && i+1<=n && j+1<=n) dp[i][j][0]=min(dp[i][j][0],dp[i][j][1]+1); } } } int main() { int n; in(n); for (int i=1; i<=n; i++) for (int j=1; j<=n; j++){ in(mp[i][j]); dp[i][j][0]=dp[i][j][1]=inf; } for (int i=0; i<=n; i++) dp[0][i][0]=dp[0][i][1]=dp[i][0][0]=dp[i][0][1]=inf; solve(n); /*for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) printf("%9d%c",dp[i][j][0],j==n?' ':' '); printf(" "); for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) printf("%9d%c",dp[i][j][1],j==n?' ':' ');*/ if (dp[n][n-1][0]>=inf) printf("-1 "); else printf("%d ",dp[n][n-1][0]); return 0; }
C.echo的画家梦想I
题目大意:给你一颗树,其中k个点被染成了黑色,问以每个点为起点经过所有黑点回到起点的最短距离是多少
Sample Input
5 2 1 3 1 2 3 2 4 3 3 5 1 4 5 1
Sample Output
8 14 10 16 8
这题是D题的强化版。。。。我建议先把D题理解了再来看C题比较好。。。
佳爷的这题的题解也写得非常详细,我们先通过自下而上的方式计算每个子树黑点对父节点的贡献,然后再自上而下计算每个非子树黑点对某个点的贡献,自下而上的黑点路径覆盖比较好求:
void dfs1(int u,int fa) {//计算子树贡献 for (int i=head[u]; i!=-1; i=eg[i].next){ int v=eg[i].to; if (v==fa) continue; dfs1(v,u); if (son[v]){//计算子树的黑点路径覆盖 dis[u]+=dis[v]+eg[i].w; } son[u]+=son[v]; } }
接下来就是通过父节点求出子节点的非子树黑点对它的贡献:
void dfs2(int u,int fa) {//计算非子树贡献 for (int i=head[u]; i!=-1; i=eg[i].next){ int v=eg[i].to; if (v==fa) continue; if (u==1){ if (son[v]){ ans[v]=dis[u]-dis[v]; if (ans[v]==eg[i].w && !black[u]) ans[v]=0;//只有v是黑点 } else ans[v]=dis[u]+eg[i].w; } else { if (son[v]){ ans[v]=dis[u]-dis[v]+ans[u]; if (ans[v]==eg[i].w && !black[u]) ans[v]=0; } else ans[v]=dis[u]+ans[u]+eg[i].w; } dfs2(v,u); } }
两个dfs理解了就很好办了,最后的答案记得*2就好了
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=5e5+10; struct node { int to,next,w; }eg[mac<<1]; int head[mac],num=0,black[mac]; long long son[mac],dis[mac],ans[mac]; void add(int u,int v,int w) { eg[++num]=node{v,head[u],w}; head[u]=num; } void dfs1(int u,int fa) {//计算子树贡献 for (int i=head[u]; i!=-1; i=eg[i].next){ int v=eg[i].to; if (v==fa) continue; dfs1(v,u); if (son[v]){//计算子树的黑点路径覆盖 dis[u]+=dis[v]+eg[i].w; } son[u]+=son[v]; } } void dfs2(int u,int fa) {//计算非子树贡献 for (int i=head[u]; i!=-1; i=eg[i].next){ int v=eg[i].to; if (v==fa) continue; if (u==1){ if (son[v]){ ans[v]=dis[u]-dis[v]; if (ans[v]==eg[i].w && !black[u]) ans[v]=0;//只有v是黑点 } else ans[v]=dis[u]+eg[i].w; } else { if (son[v]){ ans[v]=dis[u]-dis[v]+ans[u]; if (ans[v]==eg[i].w && !black[u]) ans[v]=0; } else ans[v]=dis[u]+ans[u]+eg[i].w; } dfs2(v,u); } } int main() { int n,k; memset(head,-1,sizeof head); scanf ("%d%d",&n,&k); for (int i=1; i<n; i++){ int u,v,w; scanf ("%d%d%d",&u,&v,&w); add(u,v,w);add(v,u,w); } for (int i=1; i<=k; i++){ int x; scanf ("%d",&x); son[x]=1;black[x]=1; } dfs1(1,0); //for (int i=1; i<=n; i++) printf("%d ",dis[i] ); //printf("++++ "); dfs2(1,0); for (int i=1; i<=n; i++){ printf("%lld ",(dis[i]+ans[i])*2LL); } return 0; }
D.echo的画家梦想II
题目大意:给你一颗树,其中k个点被染成了黑色,问每个点到所有黑色的最短距离和
Sample Input 1
3 3 1 2 1 2 3 4 1 2 3
Sample Output
6 5 9
emmm,我们先随便找个根节点,然后把根节点的答案算出来,接下来的子节点就可以直接通过父节点来求解了。其状态转移如下:
$dp[v]=dp[u]+eg[i].w(k-son[v])-eg[i].w(son[v])$即,子节点的答案为父节点的答案加上子节点到父节点的距离*(总的黑点-该子节点包含的黑点)-距离*(该子节点包含的黑点数)。如图:
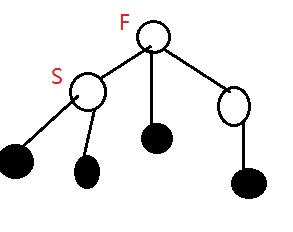
S到他子孙黑点的距离会比F更近,所以要$-eg[i].w(son[v])$,而S比F离非它子孙黑点的距离更远那么就需要$+eg[i].w(k-son[v])$
以下是AC代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int mac=5e5+10; struct node { int to,next,w; }eg[mac<<1]; int head[mac],num=0,son[mac],tot; ll ans[mac]; void add(int u,int v,int w) { eg[++num]=node{v,head[u],w}; head[u]=num; } void dfs1(int u,int fa,ll s) {//先跑一遍,获得根节点的答案和每个节点所包含的黑点数 if (son[u]) ans[1]+=s; for (int i=head[u]; i!=-1; i=eg[i].next){ int v=eg[i].to; if (v==fa) continue; dfs1(v,u,s+eg[i].w); son[u]+=son[v]; } } void dfs2(int u,int fa) { for (int i=head[u]; i!=-1; i=eg[i].next){ int v=eg[i].to; if (v==fa) continue; ans[v]=ans[u]+1LL*eg[i].w*(tot-2*son[v]); dfs2(v,u); } } int main() { memset(head,-1,sizeof head); int n,k; scanf ("%d%d",&n,&k); tot=k; for (int i=1; i<n; i++){ int u,v,w; scanf ("%d%d%d",&u,&v,&w); add(u,v,w);add(v,u,w); } for (int i=1; i<=k; i++){ int x; scanf("%d",&x); son[x]=1; } dfs1(1,0,0); dfs2(1,0); for (int i=1; i<=n; i++) printf("%lld ",ans[i]); return 0; }
E.厂里田径赛
题目大意:给你n个数,问每个数的前面有多少个数小于它
Sample Input
9 8 10 6 4 8 7 8 10 5
Sample Output
0 1 0 0 2 2 3 6 1
emmm,此题我觉得应该都会做,还不需要离散化,结果半天没人开。。。直接以值$a_{i}$为线段树的范围,得到一个值x之后直接将其丢在线段树的第x个位置即可,然后我们访问他的前面有多少个数就好了
以下是AC代码:

#include <bits/stdc++.h> using namespace std; #define lson l,mid,rt<<1 #define rson mid+1,r,rt<<1|1 const int mac=3e5+10; int a[mac],tree[mac<<2]; void update(int l,int r,int rt,int pos) { if (l==r) { tree[rt]++; return; } int mid=(l+r)>>1; if (mid>=pos) update(lson,pos); else update(rson,pos); tree[rt]=tree[rt<<1]+tree[rt<<1|1]; } int query(int l,int r,int rt,int L,int R) { if (L>R) return 0; int ans=0; if (l>=L && r<=R) return tree[rt]; int mid=(l+r)>>1; if (mid>=L) ans+=query(lson,L,R); if (mid<R) ans+=query(rson,L,R); return ans; } int main() { //freopen("in.txt","r",stdin); int n; scanf ("%d",&n); for (int i=1; i<=n; i++){ int x; scanf ("%d",&x); if (i==1) printf("0 "); else { int ans=query(1,mac-5,1,1,x-1); printf("%d ",ans); } update(1,mac-5,1,x); } return 0; }
