Andrew Ng机器学习编程作业: Linear Regression

编程作业有两个文件

1.machine-learning-live-scripts（此为脚本文件方便作业）

2.machine-learning-ex1（此为作业文件）

将这两个文件解压拖入matlab工作区内并将machine-learning-live-scripts内的ex1.mlx拖入到machine-learning-ex1ex1中

在命令提示符区输入subimit命令，并填写邮箱与提交凭证来提交作业。

1.A simple MATLAB function

修改warmUpExercise.m文件，生成5*5的单位矩阵并赋给A

 A = eye(5);

2.Linear regression with one variable（单变量线性回归）

2.1 Plotting the data

通过每个城市的人口与利润数据求人口与利润的关系。

ex1data1.txt文件内包含了数据集

加载数据并将人口数据赋给X利润数据给y

data = load('ex1data1.txt'); % read comma separated data
X = data(:, 1); y = data(:, 2);

修改plotData.m文件，填写下面的绘制代码

 plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data
  ylabel('Profit in $10,000s'); % Set the y-axis label
  xlabel('Population of City in 10,000s'); % Set the x-axis label

执行plotData(X,y)将会出面下面图

　　

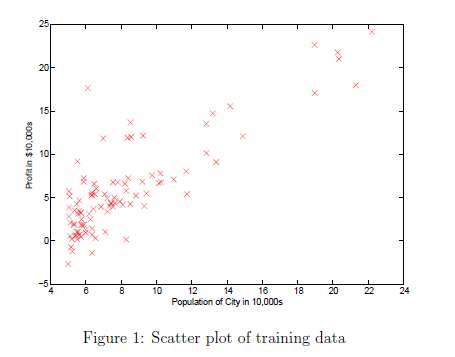
2.2 Gradient Descent

价值函数：

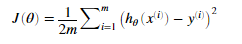
假设函数：

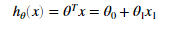
调整参数的公式是：

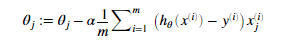
每迭代一次J的值就会减少一次。所预测的模型与实际就越符合。

初始化各个变量：

m = length(X) % number of training examples
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
iterations = 1500;
alpha = 0.01;

修改computeCost.m文件。填写代码，计算价值函数：

 J = (1/(2*m))*sum((X*theta-y).^2);

保存执行

computeCost(X, y, theta)　　

如果得到的值为32.07则表示计算正确。

修改gradientDescent.m文件，填写代码，用梯度下降算法计算theta值

temp = zeros(size(X,2),1);
　　for j = 1:size(X,2)
　　temp(j,1) = theta(j,1)-alpha*(1/m)*sum((X*theta-y).*X(:,j));
end
theta = temp;

文件中已经写好循环结构。记住一次迭代中，计算theta值需要用用当前的theta值，视频中已经说明

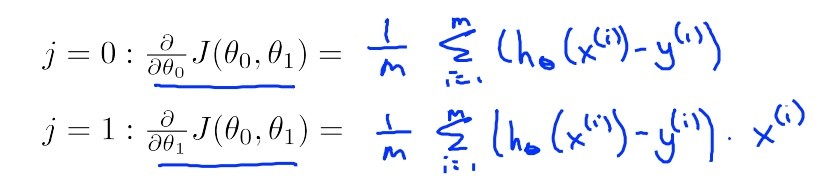
 绘制回归直线与训练集的线

% Run gradient descent:
% Compute theta
theta = gradientDescent(X, y, theta, alpha, iterations);

% Print theta to screen
% Display gradient descent's result
fprintf('Theta computed from gradient descent:
%f,
%f',theta(1),theta(2))

% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure

绘制结果：

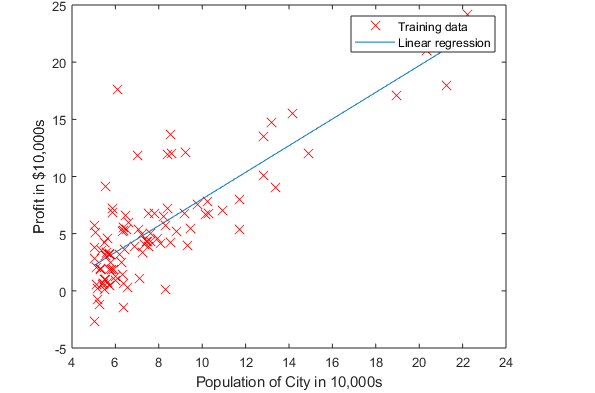
theta可视化：

价值函数的3d视图

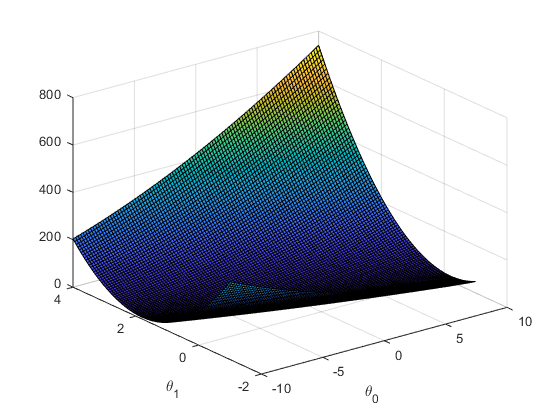
价值函数的等高线

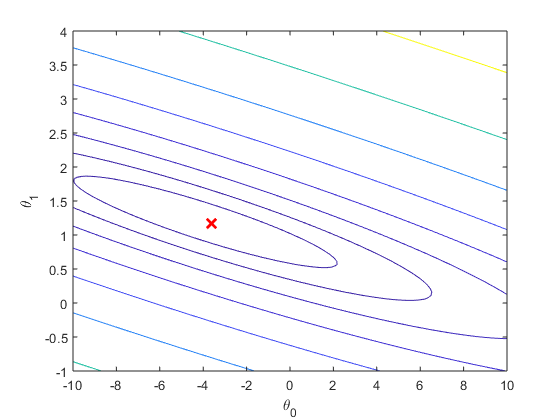
3. Linear regression with multiple variables（多变量线性回归）

多变量与单变量的价值函数相同。梯度计算也类似，只是多变量线性回归每次迭代计算的theta的数量多。

拥有房子大小和卧室数量两个特征，与房子价格。求房子价格与这两个特征的关系。

导入数据

% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);

% Print out some data points
% First 10 examples from the dataset
fprintf(' x = [%.0f %.0f], y = %.0f 
', [X(1:10,:) y(1:10,:)]');

因为房子大小与卧室数量两个值差距很大，如果直接使用梯度下降，那么收敛速度就会很慢。所以需要先进行特征缩放。

特征缩放公式：

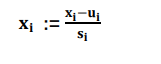
u为对对应特征平均值，s为标准差（视频中为max-min）。

修改featureNormalize.m文件，填写代码。得到正确的平均值与标准差。可以使用mean函数计算平均值，std函数计算标准差。

mu = mean(X);
sigma = std(X);
X_norm=(X-mu)./sigma;

给X添加一列1

X = [ones(m, 1) X];

在computeCostMulti.m中填写价值函数

 J = (1/(2*m))*sum((X*theta-y).^2);

价值函数也可以用下面公式表示，计算结果一样

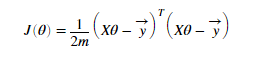
梯度下降计算theta的值将代码填入gradientDescentMulti.m文件中

 temp = zeros(size(X,2),1);
    for j = 1:size(X,2)
        temp(j,1) = theta(j,1)-alpha*(1/m)*sum((X*theta-y).*X(:,j));
    end
    theta = temp;

 计算theta的值还可是使用正规方程法。视频中有讲解

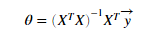
theta = pinv(X'*X)*X'*y;

预测价格：

price = [[1 ([1650 3]-mu)./sigma]*theta]

需注意，因为进行了特征缩放，所以也应该的需要预测的房子的特征进行缩放。

价格为

学习速度alpha，应该选择合适的大小。 过大可能导致价值函数不减反增。过小则会收敛太慢。