Statistical Language Model
NLP中有一个基本问题:如何计算一段文本序列在某种语言下出现的概率?这个问题在很多NLP任务中都扮演着重要的角色。统计语言模型给出了这一类问题的一个基本解决框架。对于一段文本序列:
(S=w_1,w_2,...,w_T)
它符合某种特定的语言规则的概率为:
(P(S) = P(w_1,w_2,...,w_T) = prod_{t=1}^Tp(w_t|w_1,w_2,...,w_{t-1}))
即:将序列的联合概率转化为一系列条件概率的乘积。问题变成了如何去预测这些给定previous words下的条件概率。
由于其巨大的参数空间,这样一个原始的模型在实际中应用极少。我们更多的是采用其简化版本——Ngram模型:
(p(w_t|w_1,w_2,...,w_{t-1}) approx p(w_t|w_{t-n+1},...,w_{t-1}))
即:原本我们针对一个词,需要考虑整个句子中的每个词与它之间的关联关系,现在我们只考虑与之相邻的前n-1个词与它之间的关联关系
不过,Ngram模型仍有其局限性。首先,由于参数空间的爆炸式增长,它无法处理更长程的context(N>3)。其次,它没有考虑词与词之间内在的(语义层面的)联系性。因为Ngram本质上还是将词当做一个个孤立的原子单元(atomic unit)去处理的,这种处理方式对应到数学上的形式是一个个离散的one-hot向量。显然,one-hot向量的维度等于词典的大小。这在动辄上万甚至百万词典的实际应用中,面临着严重的维度灾难问题(The Curse of Dimensionality)
Neural Network Language Model(NNLM)
鉴于Ngram等模型的不足,2003年,Bengio等人发表了一篇开创性的文章:A neural probabilistic language model。在这篇文章里,他们总结出了一套用神经网络建立统计语言模型的框架(Neural Network Language Model,以下简称NNLM),这篇文章奠定了包括word2vec在内后续研究word representation learning的基础。
NNLM针对的是这样一个问题:已知句子的前N-1个词,预测第N个词是什么。
在03年的论文里,Bengio等人采用了一个简单的前向反馈神经网络来预测第N个词((w_t))可能的条件概率(p(w_t|w_1,w_2,...,w_{t-1}))。整个模型的网络结构见下图:
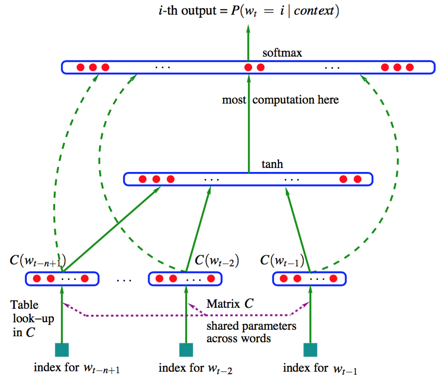
网络的工作流包括四个部分:
- 词语one-hot编码
- projection_layer层
- hidden_layer层
- SoftMax层
one-hot编码大家都很熟悉了,就是形如:[1,0,0,0,0,0...,0],[0,1,0,0,0,0...,0]的向量
projection_layer也称投影层,它是一个维度为(d imes V)的矩阵,用来把one-hot向量转化成稠密的词向量。这里的d是词向量的维数,V是词典的大小。d是可以设定的超参数。通过投影层,我们得到了n-1个词的word embedding,也就是n-1个d维的向量,把它们concat起来,就得到了这一层的输出。
接下来是hidden_layer层。这是一个fully connect layer,神经元的激活函数是tanh,参数(W_h)为((n-1) cdot d * h)的矩阵,输出为( anh(W_hcdot x + b_h)),一个长度为(h)的向量, 我们把它记为(x)
最后是SoftMax层,也被称为输出层。它的输入是:隐藏层的输出和输入层的输出之和(Ucdot anh (W_hx+b_h)+W_ox+b_o),其中(W_o)是(V*dcdot (n-1))的矩阵,(U)为(V*h)的矩阵,这里输出向量的维度为V,再通过softmax函数,每个神经元的节点即为(t)时刻出现第(i)个词的概率(P(w^i_t∣w_{t−n+1},⋯,w_{t−2},w_{t−1}))
模型的参数( heta = (U, W_h, b_h, W_o, b_o)), 损失函数:
(L = frac{1}{T} sum_t log f(w_t, w_{t-1}, ..., w_{t-n+1}; heta)+R( heta))
其中(f(w_t, w_{t-1}, ..., w_{t-n+1}))为概率(P(w_t∣w_{t−n+1},⋯,w_{t−2},w_{t−1})), (R( heta))为正则项
Word2Vec
NNLM存在的问题:
- 只能处理定长序列,缺乏灵活性
- NNLM的训练速度太慢了,无法应用于词条数目上千万甚至上亿的真实语料库
Word2Vec就是针对NNLM存在的这些问题推出的
模型分为CBOW(Continuous Bag-of-Words,词袋模型)和Skip-gram。CBOW模型的训练目标输入是某一个特定词的上下文相关的词对应的词向量,而输出的目标就是这当前特定的词的词向量,因为输入和上下文词的顺序无关,因此称为词袋模型。 Skip-Gram模型和CBOW的思路是反着来的,即输入是特定的一个词的词向量,而输出是特定词对应的上下文词向量。
接下来,我们简要介绍这两个模型的工作架构,详细的数学推导请见:word2vec 中的数学原理详解
CBOW
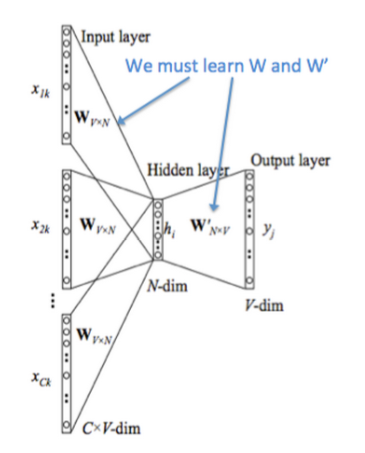
模型架构:
- 图中([x_{1k},x_{2k},...,x_{Ck}])第(k)个中心词的前后(C)个上下文的one-hot向量
- 将 one-hot 向量输入存放词向量的矩阵 (W_{V imes N})进行查表,(V)为词表大小,(W)为词向量维度
- 将查表得到的上下文向量直接进行求和,再通过一个(N imes V)的矩阵映射到输出层
对比NNLM神经语言模型,它们主要有以下三个不同点:
- 移除NNLM模型中的Hidden layer结构
- 直接将Embedding layer的查表之后累加求和(NNLM是将输出结果拼接)
- 将下文单词纳入上、下文环境,真正考虑了Context(NNLM的输入严格来说为上文文本)
Skip-gram
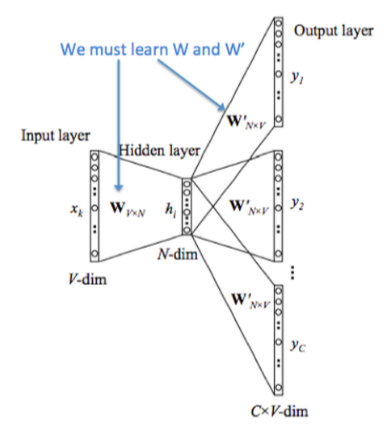
Skip-gram的模型结构与CBoW模型大同小异,也包括输入层、投影层(其实是多余的,加上该层以便与与CBoW模型对比)和输出层。
如果将Skip-gram模型的输出层的前向计算过程写成数学形式,我们得到:
(P(w_0|w_i)=frac{e^{U_0 cdot V_i}}{sum_je^{U_j cdot V_i}})
其中,(V_i)是Embedding层矩阵里的列向量,即中心词的词向量。(U_j)是softmax层矩阵里的行向量,即上下文中对应词的词向量。
Skip-gram模型的本质是计算输入word的input vector与目标word的output vector之间的余弦相似度,并进行softmax归一化。我们要学习的模型参数正是这两类词向量。
接下来我们介绍一些Word2Vec模型中的trick:
高频词降采样
对于高频词比如“的”等词,实际上对我们训练帮助不大,因此定义一个采样率:
(P(w_i)=left( sqrt{frac{z(w_i)}{0.001}} + 1 ight)cdot frac{0.001}{z(w_i)})
函数图像:

(z(w_i))表示(w_i)这个词的出现频率,(P(w_i))表示训练时对(w_i)进行采样的概率,当(z(w_i)=1)时,(P(w_i)=0.033),也就是3.3%的概率保留这个词作为训练数据,用这种方法能避免高频词大量出现在训练样本中
Hierarchical Softmax
Hierarchical Softmax是word2vec中的一项关键技术,简单来说,其通过构造一个Huffman树,将复杂的归一化概率问题转化为一系列二分类的条件概率相乘的形式。
Huffman编码又称为最优二叉树,表示一种带权路径长度最短的二叉树。带权路径长度,指的就是叶子结点的权值乘以该结点到根结点的路径长度。而我们需要构造的Huffman树结构,是以词表为根结点,每一个子节点为父节点的不相交子集,词为叶节点的结构。我们将叶节点的权值转化为词频,则带权路径长度指的就是词频乘以路径的大小,带权路径最小的条件使得构造出来的霍夫曼树中,高频词离根结点更近,而低频词离根结点更远。其构造的Huffman树如下所示:
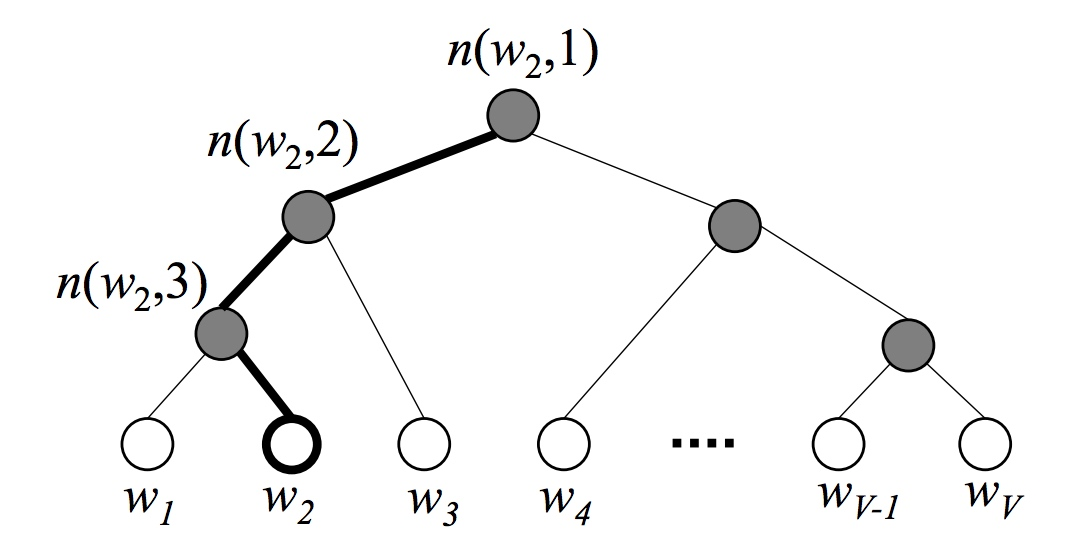
在构建Huffman树的同时,会为每一个非叶子节点初始化一个向量,该向量用于与预测向量求条件概率,假设我们的根结点表示原始字典D,则第二层的两个子节点表示D的两个子集(D_1)和(D_2),则在给定context的条件下,目标词(w_t)属于(D_1)的条件概率可以转换为一个二分类的逻辑回归函数:
(p(w_t in D_1|context)=frac{1}{1+e^{-U_{D_{root}} cdot V_{w_t}}})
当走到一个子节点后,我们又用类似的方法再对其进行二分类,得到下一个二分类的条件概率。假设每当我们将其分为左子节点时记为0,将其分为右子节点时记为1,则可以将最后的路径的用0,1组合的二叉树编码表示,相应的似然函数为:
(p(w_t|context)=p(D_1=1|context)p(D_2=0|D_1=1)dots p(w_t|D_k=1))
这样,我们可以通过最大化这个似然函数来求解二叉树上的参数——非每一个叶节点上的向量,用来计算游走到某一个子节点的概率。
层次Softmax是一个很巧妙的模型。它通过构造一颗二叉树,将目标概率的计算复杂度从最初的(V)降低到了(log_2V)的量级。不过付出的代价是人为增强了词与词之间的耦合性。例如,一个word出现的条件概率的变化,会影响到其路径上所有非叶节点的概率变化,间接地对其他word出现的条件概率带来不同程度的影响。因此,构造一颗有意义的二叉树就显得十分重要。实践证明,在实际的应用中,基于Huffman编码的二叉树可以满足大部分应用场景的需求。
Negative Sampling
与改造模型输出概率的Hierarchical Softmax算法不同,NCE算法改造的是模型的似然函数。其思想来源于一种叫做噪声对比估计(Noise-Contrastive Estimation)的算法。
以Skip-gram模型为例,其原始的似然函数对应着一个多项分布。在用最大似然法求解这个似然函数时,我们得到一个cross-entropy的损失函数:
(J( heta)=-frac{1}{T}sum_{t=1}^T{sum_{-c leq j leq c, j eq 0}{log p(w_{t+j}|w_t)}})
式中的(p(w_{t+j}|w_t))是整个字典归一化了的概率。
NCE算法中,我们构造了这样一个问题:对于一组训练样本,我们想知道,目标词的预测,是来自于context的驱动,还是一个事先假定的背景噪声的驱动?显然,我们可以用一个逻辑回归的函数来回答这个问题:
(p(D=1|w, context)=frac{p(w|context)}{p(w|context)+kp_n(w)}=sigma (log p(w|context) - log kp_n(w)))
这个式子给出了一个目标词(w)来自于context驱动的概率。其中,(k)是一个先验参数,表明噪声的采样频率。(p(w|context))是一个非归一化的概率分布,可以看作是softmax归一化函数中的分子部分。(p_n(w))则是背景噪声的词分布,通常采用word的unigram分布。而(sigma (⋅))是我们熟悉的sigmoid函数
在Mikolov论文中的负采样算法,是NCE的简化版本。简单来说,其正负采样过程具有以下两个步骤:
- 首先确定正样本,通过计算中心词与上下文中词的其余弦相似度,再用一个sigmoid函数来判断:(p(D=1|w_o, w_i)=sigma (U_o cdot V_i))
- 采样词典中不在中心词上下文中的词的词作为负样本,采样频率由该词在语料库中出现的频率有关,作者给出了一个经验公式:(P(w_i) = frac{f(w_i)^{3/4}}{sum^n_{j=0}(f(w_j)^{3/4})})
其中,(f(w_i))是该词在语料库中的出现频率,一共采样k个词
经过这样的采样操作后,我们得到一个新的数据集。其中,label标记了数据的来源(正例被标记为1,负例被标记为0)。在这个新的数据集上,我们仅需要从采样结果中计算计算归一化概率分布,从而大大简化计算过程。
【参考】