思路以dist数组 来扩充 路径的访问,不断的刷新dist数组
设置一个顶点的集合s,并不断地扩充这个集合,一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点,并且调整非s中点的最短路径长度,找当前最短路径点,将其加入到集合s,直到终点在s中。
基本步骤:
1、把所有结点分成两组:
第一组:包括已经确定最短路径的结点;
第二组:包括尚未确定最短路径的结点。
2、开始时,第一组只包含起点,第二组包含剩余的点;
3、用贪心的策略,按最短路径长度递增的顺序把第二组的结点加到第一组去,直到v0可达的所有结点都包含于第一组中。在这个过程中,不断更新最短路径,总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。
4、每个结点对应一个距离值,第一组结点对应的距离就是v0到此结点的最短路径长度,第二组结点对应的距离值就是v0由第一组结点到此结点的最短路径长度。
5、直到所有的顶点都扫描完毕(v0可达的所有结点都包含于第一组中),找到v0到其它各点的所有最短路径。
如图:求0点到其他点的最短路径。
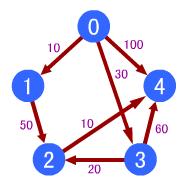
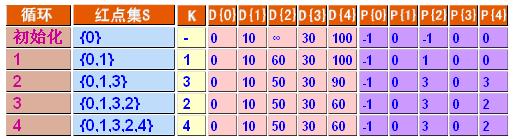
(1)开始时,s1={v0},s2={v1,v2,v3,v4},v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中,最短路径为v1,因此s1={v0,v1},由于v1到v2有路径,因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中,最短路径为v3,因此s1={v0,v1,v3},由于v3到v2、v4有路径,因此v0到各点的最短路径更新为{0,10,50,30,90};
(4)在还未进入s1的顶点之中,最短路径为v2,因此s1={v0,v1,v3,v2},由于v2到v4有路径,因此v0到各点的最短路径更新为{0,10,50,30,60};
数据结构:
(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离,0x7fffffff表示无通路:
(2)用数组dist[i..j]表示最短路径;
(3)用集合s表示找到最短路径的结点。
<转 http://www.cnblogs.com/Soul-ice-ACM/articles/2140221.html >
松弛原理
#include<cstdio> #include<queue> #include<vector> #include<map> #include<string> #include<iostream> #include<cmath> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; #define INF 0x7fffffff #define LL __int64 const int maxn=105; int mpt[maxn][maxn]; int vis[maxn]; int m,n; int dist[maxn];//从起点到其他点的最短距离 int dijkstra() { int start,end; start=1;end=n; for(int i=1;i<=n;i++) dist[i]=mpt[start][i]; vis[1]=1; while(true) { //第一步 //找出与起点集合相连的最短边 int minx=INF; int v; for(int i=1;i<=n;i++) { if(dist[i]<minx&&vis[i]==0) { minx=dist[i]; v=i; } } if(minx>=INF)break;//如果所有点都在起点集合内 vis[v]=1; //松弛、更新DIST数组 for(int i=1;i<=n;i++) { if(vis[i]==0&&dist[i]>dist[v]+mpt[v][i]&&dist[v]<INF&&mpt[v][i]<INF) { dist[i]=dist[v]+mpt[v][i]; } } } return dist[end]; } void init() { memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j)mpt[i][j]=0; else mpt[i][j]=INF; } } } int main() { while(scanf("%d%d",&n,&m)!=EOF) { if(n==0&&m==0)break; init(); //建图 for(int i=1;i<=m;i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c); if(c<mpt[a][b]) { mpt[a][b]=c; mpt[b][a]=c; } } printf("%d ",dijkstra()); } return 0; }