ACM中的矩阵优化总结

一、矩阵相乘

　　设C,A,B三个矩阵，C = A * B

　　则C[i][j] = ∑A[i][k] * B[k][j] （k = 0，1，2，...n-1）

　　矩阵相乘就是这么算的，依次用前面矩阵的每一行，依次乘后面矩阵的每一列，i就是行，j就是列。所以矩阵相乘就不满足交换律。

　　实现 ： 3个变量，3重for循环。

二、矩阵快速幂（仿二分快速幂）　　

　　计算Aⁿ ：

　　将矩阵TEMP置为E单位矩阵

　　if n为奇数

　　　 TEMP = TEMP * A ;

　　　 n--;

　　if n为偶数

　　　 A = A  * A ;

　　　 n /= 2;

　　循环到n为0，TEMP就是答案

　　//10⁹也承受不住30多次除2，时间复杂度0(logn * N³)，N为矩阵阶数（N*N矩阵），这样的话100阶矩阵也有超时的危险。

 　　

　　  推荐题目 ： http://poj.org/problem?id=3233

　  解题报告 ： 点这里 (代码写的很一般)

三、矩阵优化递推式

　　F（n）= A * F（n-1）

　　上面都是矩阵，根据矩阵的结合律，这个式子可以化为F（n）= A^n-1 * F（1）

　　这样求A^n-1用矩阵快速幂去求，计算原问题的时间复杂度就从0(n)优化成了O(logn)。

　　一般难点是在怎么化为标准的式子（方程组化为矩阵）

　　题目链接 ： http://acm.nyist.net/JudgeOnline/problem.php?pid=301

　　题目描述 ：

　　　　给你一个递推公式：f(x)=a*f(x-2)+b*f(x-1)+c，并给你f(1),f(2),a,b,c的值，请求出f(n)的值，由于f(n)的值可能过大，求出f(n)对1000007取模后的值。

 　　　   注意 : -1对3取模后等于2，1<=n<=100000000 (10^9)

　　解析 ：

　　化为标准式只有一个原则，F（n）的每个变量i，都对应着F（n-1）的每个变量i-1，有常量项就都为1。

　　举个栗子，看题目的递推公式，显然左边还缺了个x-1来对应右边的x-2，所以

　　　　　　　　　　　f(x) = a*f(x-2)+b*f(x-1)+c*1

　　　　　　　　　　f(x-1) = 0*f(x-2)+b*f(x-1)+0*1

　　　　　　　　　　　　1 = 0*f(x-2)+0*f(x-1)+1*1

　　将这个方程组化为矩阵

　　

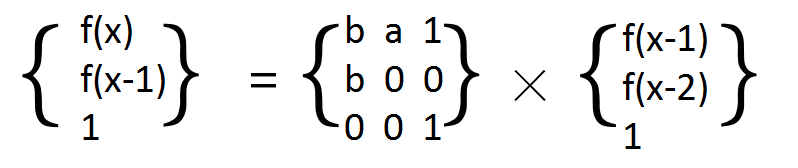
　　再化

　　

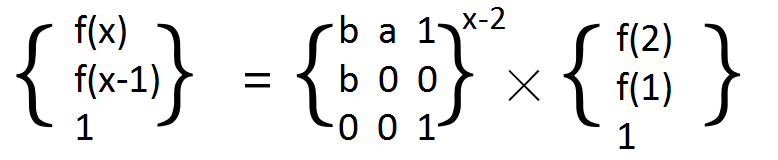
　　就OK了！

　　*优化求斐波那契项是不是就很简单了

　　*推荐题目 ： http://acm.hdu.edu.cn/showproblem.php?pid=5950

　　  *对一个二维dp的优化，题目链接 ： 点这里

　　　dp分析：dp[i][j] = ( dp[i-1][j] + dp[i-1][j-1] )%2   //i表示第i秒，j表示第j个灯，注意下j=0的情况

　　　　　　这个就不能像前面一样，二维，而且j变量就根本不能那样处理。。。。。

　　　　　　所以...

　　　　　　枚举j，如果0≤j≤N。

　　　　　　dp[i][0] = ( dp[i-1][0] + dp[i-1][N] )%2

　　　　　　dp[i][1] = ( dp[i-1][1] + dp[i-1][0] )%2

　　　　　　......

　　　　　　dp[i][N] = ( dp[i-1][1] + dp[i-1][N-1] )%2

　　　　　　好像每次换一排灯，每个方程改变一个灯　　　　

四、其它应用

　　1，转换

　　有些转换可以等价于乘上了一个矩阵，那么多次转换就好像依次乘了几个矩阵，然后再用结合律...