8-1 非线性假设
神经网络实际上是一个很古老的算法,为什么要学习这个算法呢
假如我们有一个监督学习分类问题,以下的例子只有两个特征项

无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大。

比如像这样的项会非常多,甚至会呈指数式增长
假设我们希望训练一个模型来识别视觉对象(例如识别一张图片上是否是一辆汽车),我们怎样才能这么做呢?一种方法是我们利用很多汽车的图片和很多非汽车的图片,然后利用这些图片上一个个像素的值(饱和度或亮度)来作为特征。
假如我们只选用灰度图片,每个像素则只有一个值(而非 RGB值),我们可以选取图片上的两个不同位置上的两个像素,然后训练一个逻辑回归算法利用这两个像素的值来判断图片上是否是汽车:
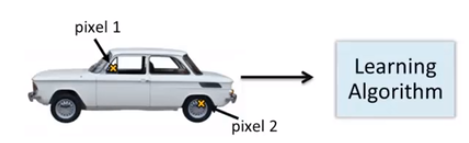
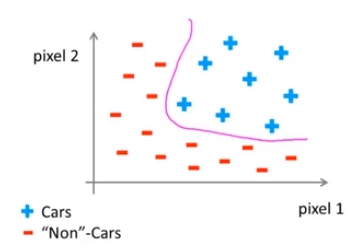
假使我们采用的都是50x50像素的小图片,并且我们将所有的像素视为特征,则会有 2500个特征,如果我们要进一步将两两特征组合构成一个多项式模型,则会有约个25002/2(接近3百万个)特征,普通的逻辑回归模型,不能有效地处理这么多的特征,这时候我们需要神经网络。

8-2 神经元与大脑
神经网络是一种很古老的算法,它最初产生的目的是制造能模拟大脑的机器。
他能够很好的解决不同的机器学习问题
我们能学习数学,学着做微积分,而且大脑能处理各种不同的令人惊奇的事情。似乎如果你想要模仿它,你得写很多不同的软件来模拟所有这些五花八门的奇妙的事情。不过能不能假设大脑做所有这些,不同事情的方法,不需要用上千个不同的程序去实现。

大脑的这一部分这一小片红色区域是你的听觉皮层,你现在正在理解我的话,这靠的是耳朵。
把耳朵到听觉皮层的神经切断。在这种情况下,将其重新接到一个动物的大脑上,这样从眼睛到视神经的信号最终将传到听觉皮层。
这块红色的脑组织是你的躯体感觉皮层,这是你用来处理触觉的,
神经网络可能为我们打开一扇进入遥远的人工智能梦的窗户,但我在这节课中讲授神经网络的原因,主要是对于现代机器学习应用。它是最有效的技术方法。因此在接下来的一些课程中,我们将开始深入到神经网络的技术细节。
8-3 模型展示1
我们的大脑中充满了这样的神经元,其中有两点值得注意,一个是神经元的细胞体,二是细胞体上的树突(神经元的通道)神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
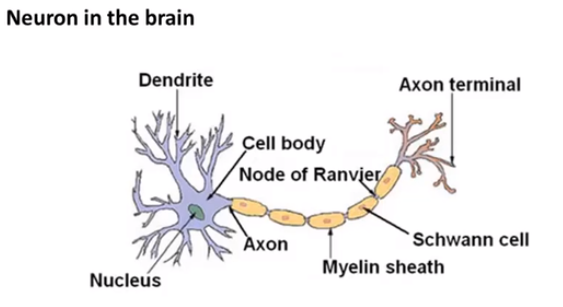
下面是一组神经元的示意图,神经元利用微弱的电流进行沟通。这些弱电流也称作动作电位,其实就是一些微弱的电流。所以如果神经元想要传递一个消息,它就会就通过它的轴突,发送一段微弱电流给其他神经元,这就是轴突。(这些是我们高中生物学的知识)
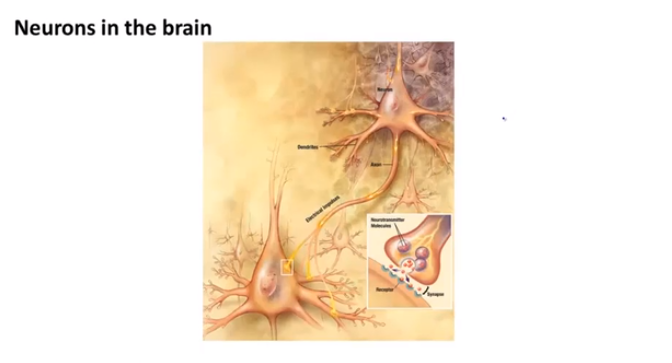
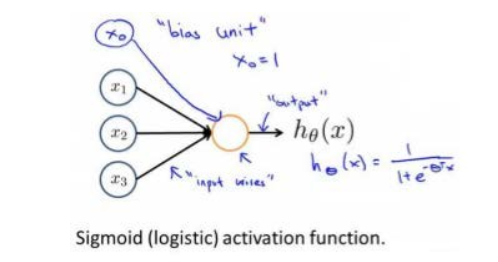
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被成为权重(weight)。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit)
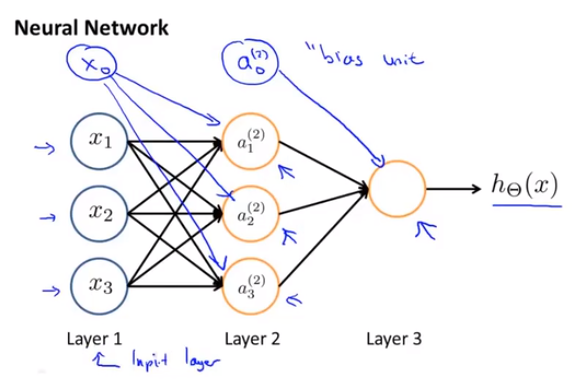
接下来让我们逐步呈现上图的计算步骤:
下面引入一些标记法来帮助描述模型:ai(j) 代表第 j 层的第 i 个激活单元。代表从 θ(j) 第 j 层映射到第 j+1 层时的权重的矩阵,例如 θ(1) 代表从第一层映射到第二层的权重的矩阵。
其尺寸为:以第 j+1 层的激活单元数量为行数,以第 j 层的激活单元数加一为列数的矩阵。
例如:上图所示的神经网络中的尺寸为 3*4。
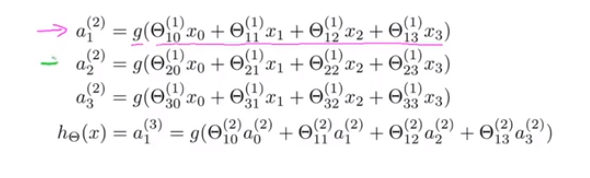
我们可以知道:每一个都是由上一层所有的和每一个所对应的决定的。(我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION ))

这样我们就可以得到 θ * X = a
8-4 模型展示2
这一节我们主要来讲解以上式子的含义
具体内容请观看:https://www.bilibili.com/video/BV164411S78V?p=46
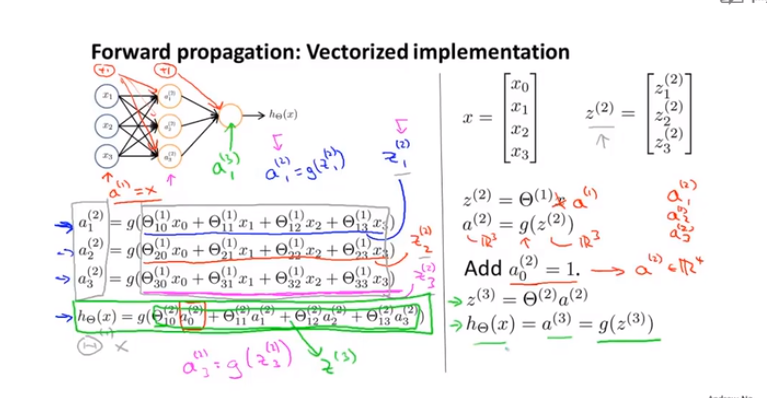
这里的x1,x2,x3表示的是一个样本中的三个特征
以下是更好理解的方法
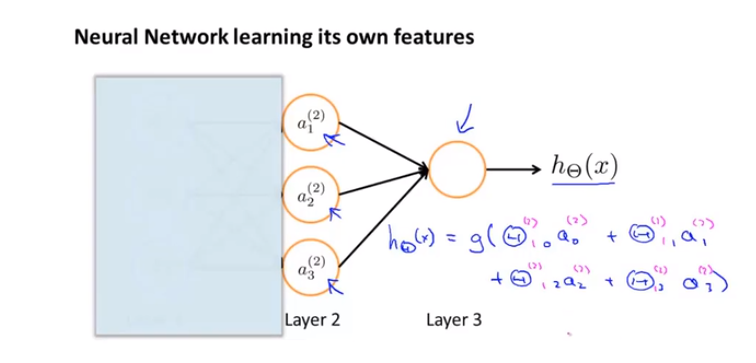
8-5 例子与直觉理解1
以下的例子可以可看作真值表的计算


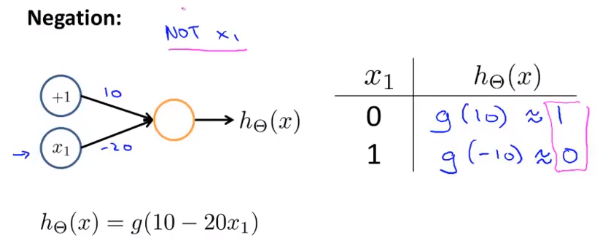
8-6 例子与直觉理解2
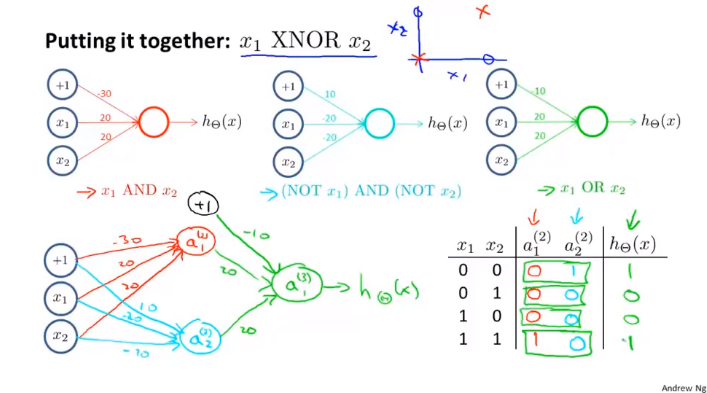
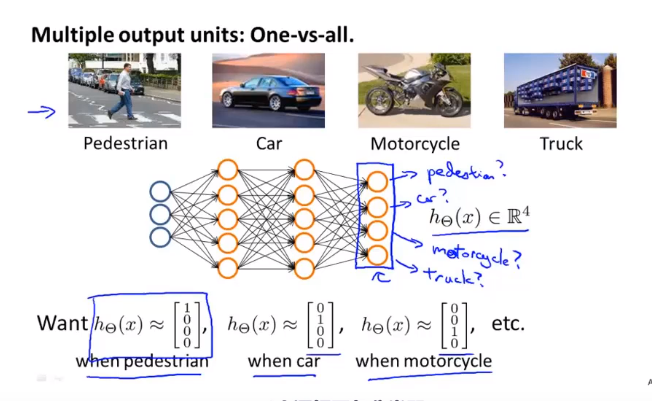
8-7 多元分类