浅谈树状数组

大概是最简单的数据结构了，我超喜欢的……

一、引入

前缀和的题目想必是非常常见了

给你n个数，如果修改了第i个数，那么第i,i+1……n个数的前缀和都要修改

用暴力的话，需要O(n)的时间复杂度

如果有m次修改的话，O(MN)的时间复杂度分分钟TLE

用树状数组呢？仅为O(MlogN)。也就是说，每次修改只需要logN的复杂度

二、简介

从引入中可以看出，树状数组主要用来解决维护数组前缀和的问题

它为什么这么快？

因为它用了二进制来维护

比如11，11=(1011)₂

so,11=2³+2¹+2⁰

也就是说，区间[1,11]可以进行分解：[1,2³],[2³+1,2³+2¹],[2³+2¹+1,2³+2¹+2⁰]

我们如果知道了这三段区间的值，就可以在logn的时间下求出[1,11]这个区间的和

三、结构

首先引入一个函数，lowbit

干嘛用的呢？

观察上面例子中的三个区间

[1,2³],区间长度为8，2³=8

[2³+1,2³+2¹]区间长度为2，2¹=2

[2³+2¹+1,2³+2¹+2⁰]区间长度为1，2⁰=1

我们可以发现，每一段区间的长度就等于区间末尾那个数二进制形式下最低位的1所代表的数（或者说，二进制分解下的最小次幂）

我们用lowbit(i)来表示这个东西

就如同我们可以用三个区间来表示[1,11]这个区间前11个数的和一样，给一个数组a，我们都可以用一个数组c来维护a的前缀和

这个数组c就是树状数组啦

它长这样：

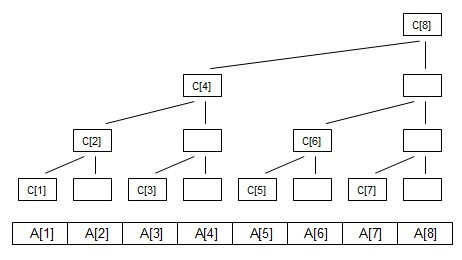
（图片来源于https://www.cnblogs.com/hsd-/p/6139376.html）

 其中，

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

每个c[x]的父亲都是c[x+lowbit(x)]

 

四、算法流程

 

1.求lowbit(x)

比如一个二进制数11001000，怎么求它的lowbit呢？

我们给它按位取反：

00110111

然后再加一：

00111000

然后我们发现，这个数跟原数只有最低位的1相同，其他都不同

与一下就OK了

注：~n+1=-n（~n表示n的按位取反，-n表示n的补码）

代码如下：

int low_bit(int x)
{
    return x&(-x);
}

2.单点修改

这个挺好理解，由于c[x]的父亲是c[x+lowbit(x)]，那么如果修改x的值，一直x+=lowbit(x)并修改就可以了

代码如下：

void add(int x)
{
    while(x<=MAXX)//MAXX为x的理论最大值，视题目具体情况而定
    {
        c[x]++;
        x+=low_bit(x);
    }
}

3.区间查询

现在，询问a[l,r]的和

由于c数组是维护前缀和的，问题可以转化为求前r个数的和减前l-1个数的和

同理，由于c[x]的父亲是c[x+lowbit(x)]，所以c[x]的儿子是c[x-lowbit(x)]。那么求前x个数的和话，一直x-=lowbit(x)直到x=0并求和就可以了

代码如下：

int find(int x)
{
    int res=0;
    while(x>0)
    {
        res+=c[x];
        x-=low_bit(x);
    }
    return res;
}

五、扩展

一维的树状数组可以扩展为二维的

这里不做讲解了，代码如下

单点修改：

void add(int x,int y,int k)
{
    int i=x;
    while(i<=n)
    {
        int j=y;
        while(j<=m)
        {
            c[i][j]+=k;
            j+=low_bit(j);
        }
        i+=low_bit(i);
    }
}

区间查询：

int find(int x,int y)
{
    int res=0,i=x;
    while(i>0)
    {
        int j=y;
        while(j>0)
        {
            res+=c[i][j];
            j-=low_bit(j);
        }
        i-=low_bit(i);
    }
    return res;
}

注意，lowbit取的值不能为0！不能为0！不能为0！因为lowbit(0)=0，这样的话程序就完蛋了

板子：

洛谷P3374

 AC代码（仅供参考）：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;

inline int read()
{
    int f=1,x=0;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}

int n,m;
long long c[1000005]; 

int low_bit(int x)
{
    return x&(-x);
} 

void add(int p,int x)
{
    while(p<=n)
    {
        c[p]+=x;
        p+=low_bit(p);
    }
}

long long find(int p)
{
    long long num=0;
    while(p>0)
    {
        num+=c[p];
        p-=low_bit(p);
    }
    return num;
}

int main()
{
    n=read(); m=read();
    int k,x,y;
    for(int i=1;i<=n;i++)
    {
        x=read();
        add(i,x);
    }
    for(int i=1;i<=m;i++)
    {
        k=read(); x=read(); y=read();
        if(k==1) add(x,y);
        else printf("%lld
",find(y)-find(x-1));
    }
    return 0;
}

本文部分图片来源于网络

部分内容参考《信息学奥赛一本通.提高篇》第四部分第一章 树状数组

若需转载，请注明https://www.cnblogs.com/llllllpppppp/p/9866826.html

~NOIP2018 加油~