题目来源:http://www.patest.cn/contests/mooc-ds/04-%E6%A0%916
In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer N (2 <= N <= 63), then followed by a line that contains all the N distinct characters and their frequencies in the following format:
c[1] f[1] c[2] f[2] ... c[N] f[N]
where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer M (<=1000), then followed by M student submissions. Each student submission consists of N lines, each in the format:
c[i] code[i]
where c[i] is the i-th character and code[i] is a string of '0's and '1's.
Output Specification:
For each test case, print in each line either “Yes” if the student’s submission is correct, or “No” if not.
Sample Input:
7 A 1 B 1 C 1 D 3 E 3 F 6 G 6 4 A 00000 B 00001 C 0001 D 001 E 01 F 10 G 11 A 01010 B 01011 C 0100 D 011 E 10 F 11 G 00 A 000 B 001 C 010 D 011 E 100 F 101 G 110 A 00000 B 00001 C 0001 D 001 E 00 F 10 G 11
Sample Output:
Yes Yes No No
题目大意:通过给定的字符及其访问次数,判断给定的编码是否为哈夫曼编码
判断条件:满足条件的编码形成的哈夫曼树可能不同,但其带权路径长度WPL一定相同且最小;且满足前缀码(前缀码是任何字符的编码都不是另一字符编码的前缀,前缀码可以避免二义性)
解题思路:
1.根据输入的节点(字符)以及权重(访问次数),模拟建立哈夫曼树,并求出其WPL
a.把权重建成一个最小堆(数组实现),然后每次弹出最小堆的最小元素即根节点
b.构造一个新的节点:从堆中依次弹出两个最小的元素的和作为新节点的权重,再将新节点插入堆中
c.WPL的值就是所有新节点的权重的和
2.根据输入的编码计算WPL用来判断是否与哈夫曼树的WPL相同
WPL等于每个字符编码访问次数与编码长度的乘积之和
3.根据输入的编码判断是否为前缀码
双重循环遍历,判断两个字符中某一个字符编码是否是另一个字符编码的前缀
图解建立哈夫曼树的过程中最小堆与哈夫曼树的变化如下:
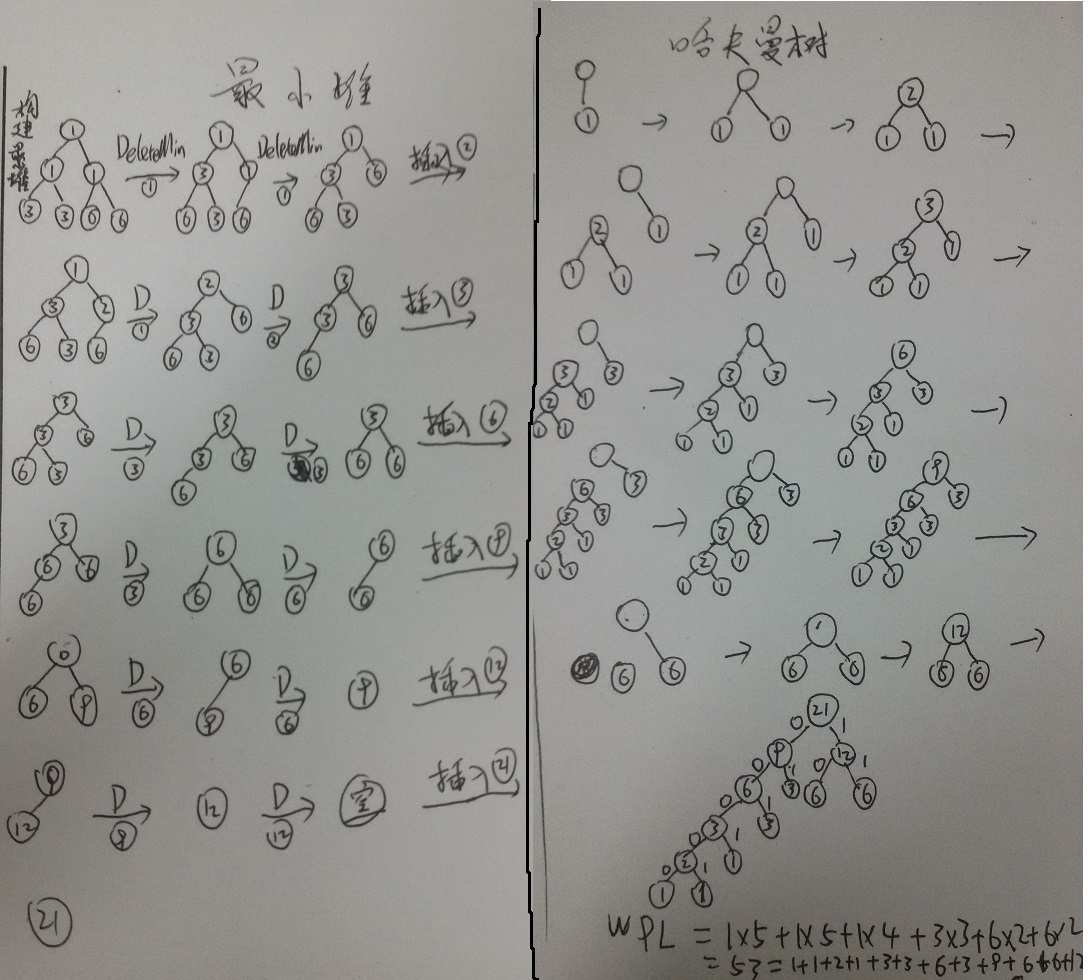
代码如下:
#include <cstdio> #include <cstdlib> #include <cctype> #include <cstring> #define N 64 //最大字符数 #define M 200 //最大编码长度 int HuffmanWPL(int heap[]); /*模拟建立哈夫曼树,返回WPL*/ void PercolateDown(int heap[], int *Size, int parent); /*从节点parent开始下滤*/ void BuildMinHeap(int heap[], int *Size); /*通过传入的完全二叉树(数组)建立最小堆*/ int DeleteMin(int heap[], int *Size); /*删除堆中最小元素 */ void Insert(int minHeap[], int * Size, int weight); /*向最小堆中插入权重为weight的节点*/ int CountWPL(int f[], char code[][M]); /*计算一种编码的WPL*/ bool IsPrefixcode(char code[][M]); /*判断某种编码是否为前缀码*/ bool IsPrefix(char *s1, char *s2); /*判断两个字符中某一个字符编码是否是另一个字符编码的前缀*/ int n; //全局变量,字符的个数 int main() { char ch, code[N][M]; int f[N]; scanf("%d", &n); for (int i = 1; i <= n; i++) { while(ch = getchar()) { if (isalpha(ch) || isdigit(ch) || ch == '_') { //如果是字符 scanf("%d", &f[i]); //输出对应的访问次数 break; } } } int minWPL = HuffmanWPL(f); //通过模拟哈夫曼树得到最小WPL int stusNum; //学生个数(编码种类) scanf("%d", &stusNum); for (int i = 0; i < stusNum; i++) { for (int j = 1; j <= n; j++) { while(ch = getchar()) { if (isalpha(ch) || isdigit(ch) || ch == '_') { //若为字符 scanf("%s", code[j]); //输入对应字符的编码 break; } } } int thisWPL = CountWPL(f, code); if (thisWPL == minWPL && IsPrefixcode(code)) //若WPL为最小且为前缀码 printf("Yes "); else printf("No "); } return 0; } bool IsPrefixcode(char code[][M]) { for (int i = 1; i <= n; i++) for (int j = i+1; j <= n; j++) if (IsPrefix(code[i], code[j])) return false; return true; } bool IsPrefix(char *s1, char *s2) { while (s1 && s2 && *s1 == *s2) { //从编码首位向后遍历,当遍历到末端或两者不相等时退出循环 s1++; s2++; } if (*s1 == '�' || *s2 == '�') //若遍历到某个字符编码的末端 return true; //则该字符是另一字符的前缀 else return false; } int CountWPL(int f[], char code[][M]) { int WPL = 0; for (int i = 1; i <= n; i++) WPL += f[i] * strlen(code[i]); //权重*编码长 return WPL; } void PercolateDown(int heap[], int *Size, int parent) { int temp = heap[parent]; int i, child; for (i = parent; i*2 <= (*Size); i = child){ child = 2 * i; if (child != (*Size) && heap[child+1] < heap[child]) //找到值更小的儿子 child++; if (temp > heap[child]) //如果值比下一层的大 heap[i] = heap[child]; //下滤 else break; } heap[i] = temp; } void BuildMinHeap(int heap[], int *Size) { for (int i = (*Size) / 2; i > 0; i--) //从最后一个有儿子的节点开始 PercolateDown(heap, Size, i); //向前构造最小堆 } int DeleteMin(int heap[], int *Size) { int minElem = heap[1]; //最小堆根节点为最小值 heap[1] = heap[*Size]; //将最小堆最后一个节点放到根节点处 (*Size)--; //节点数减一 PercolateDown(heap, Size, 1); //从根节点开始下滤 return minElem; } void Insert(int heap[], int * Size, int weight) { int i; for (i = ++(*Size); i > 0 && heap[i/2] > weight; i /= 2) //先将要插入的节点放最后 heap[i] = heap[i/2]; //再上滤 heap[i] = weight; } int HuffmanWPL(int heap[]) { int minHeap[N]; int Size = 1; for (int i = 1; i < n; i++) minHeap[Size++] = heap[i]; //将构造最小堆的数组初始化 minHeap[Size] = heap[n]; BuildMinHeap(minHeap, &Size); int WPL = 0; for (int i = 1; i < n; i++) { int leftWeight = DeleteMin(minHeap, &Size); int rightWeight = DeleteMin(minHeap, &Size); int rootWeight = leftWeight + rightWeight; WPL += rootWeight; Insert(minHeap, &Size, rootWeight); } return WPL; }