哎,是我太天真......
T1:integer
大致思路:在模拟二进制时,在加进位时可以看成找一群1中的0,把0左边的1区间反转(111110)
在树上:不断的把标记往上传,传时,看父亲的右子树有没有0,没有就反转,直到找到叶子结点0
需要用到三个标记:ret:加到当前位需要进位
2.cover:全部变为0还是1
3.all:全部变为0还是1
快速乘:
inline ll ksc(ll x,ll y,ll p){//计算x乘y的积
ll res=0;//加法初始化
while(y){
if(y&1)res=(res+x)%p;//模仿二进制
x=(x<<1)%p;
y>>=1;//将x不断乘2达到二进制
}return res;
}
快速乘基本原理:
由于计算机底层设计的原因,做加法比乘法快,在大数乘法时最好把乘法转化为加法提高运算速度,此外,当我们计算
(a*b)mod m 时,可能a*b越过了long long 的范围,可以用快速乘解决此问题。
快速乘就是利用二进制和乘法分配律来将a*b转化为多个式子相加的形式求解,(使用时将第二个乘数转化为二进制的形式)。
举个例子:
20*14=20*(1110)2 = 20*(2^3)*1 +20*(2^2)*1 + 20*(2^1)*1 +20*(2^0)*0=160+80+40=280 ;
14=8+4+2; 代码中 b&1 取最低位,b>>=1 ,去掉最低位,
a每次循环均 * 2,循环直到b=0 ,就是从右到左模拟上述过程。不多说了,看代码。O(logn)
T2:play
2011noip普及组的瑞士轮
大致思路:关键在于快排O(nlogn)的时间复杂度要超,就可以考虑将三种不同类型的改动,分别放入三个序列中,从而构造两个新的数列,来比较三次,从而将较大的数放入最终的新数列中(就像三个整数来取较大数一样)
T3: (哇,之前liu_runda还讲过一次)
大致思路:
没想到啊,是带权并查集(来维护各列的差值)
通过不断地模拟我们可以发现以下性质:
1.r2-r1=l2-l1;
2.同一行的两个元素即不同列,每相邻列间的差值一定都是一样的(由1得)只要给了你任意两列的数的差值,则可以推出所有列要放的话应满足的数
考虑怎样才不能放:
1.本身填的数为负数
2.在推的过程中出现负数:比较巧的是选了一个基准夹在当前点与推的那个点间,怎样会可能产生负数呢?由一个较小的数,且差值大
3.填不进去不满足性质2
注意:
1.在推可能不满足时,需要行列来分别看(毕竟差的不一样),但最终推负值时只用枚举行列中的一个即可
关于带权并查集:
对于每个权值我们维护的是到根的路径长度:所以当合并的时候,我们要把那个fa变的当前的点得权值更新一下
怎么更新?
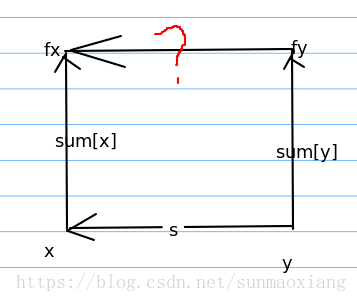
sum[x]+s=sum[y]+sum[fy]
可以看到每连一条边,深度就是一样的,当然用向量理解也是没有毛病的
sum[fy]=sum[x]+s-sum[y] (sum【x】- sum【y】+ s)