agc027_d Modulo Matrix

agc027_d Modulo Matrix

https://atcoder.jp/contests/agc027/tasks/agc027_d

Tutorial

https://img.atcoder.jp/agc027/editorial.pdf

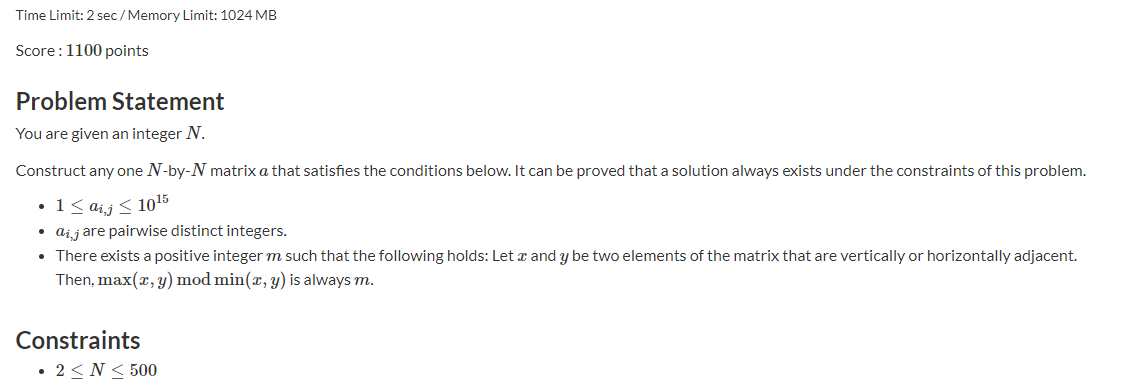
想办法去掉(max,min).由于是网格图,所以棋盘染色,然后在黑色格子上添一些数字,白色格子上的数字就是周围黑色格子上的数字的lcm+1.

考虑在黑色格子上添什么数,才可以让白色格子上的数尽量小.由于最后是取lcm,且每个黑色格子是独特的两条对角线交点,那么给每个对角线分配一个素数,令黑色格子为它所在两个对角线的素数的积.则最后白色格子上的数会是4个素数的积.勉强满足条件.

Code

https://atcoder.jp/contests/agc027/submissions/15106276

#include <cstdio>
#include <iostream>
#include <map>
#include <vector>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define value0(a) prime[(a)-1]
#define value1(b) prime[(b)+749]
using namespace std;
inline char gc() {
	return getchar();
	static char buf[100000],*l=buf,*r=buf;
	return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void rd(T &x) {
	x=0; int f=1,ch=gc();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
	while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=gc();}
	x*=f;
}
typedef long long ll;
const int maxn=500+5;
const int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
int n;
int val0[maxn<<1],val1[maxn<<1];
ll an[maxn][maxn];
bool mark[10005];
vector<int> prime; 
ll gcd(ll a,ll b) {return b==0?a:gcd(b,a%b);}
void init(int n) {
	for(int i=2;i<=n;++i) {
		if(!mark[i]) {
			prime.push_back(i);
		}
		for(int j=0;j<prime.size();++j) {
			int x=i*prime[j]; if(x>n) break;
			mark[x]=1;
			if(i%prime[j]==0) break; 
		}
	}
}
int main() {
	rd(n);
	if(n==2) {puts("4 7
23 10"); return 0;} 
	init(10000);
	for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) if((i+j)%2==0) {
		an[i][j]=value0((i+j)/2)*value1((i-j)/2);
	}
	for(int x=1;x<=n;++x) for(int y=1;y<=n;++y) if((x+y)&1) {
		an[x][y]=1;
		for(int k=0;k<4;++k) {
			int _x=x+dx[k],_y=y+dy[k];
			if(_x<1||_x>n||_y<1||_y>n) continue;
			an[x][y]=an[x][y]/gcd(an[x][y],an[_x][_y])*an[_x][_y];
		}
		++an[x][y]; 
	}
	for(int i=1;i<=n;++i) {
		for(int j=1;j<=n;++j) {
			if(j!=1) printf(" ");
			printf("%lld",an[i][j]);
		}
		printf("
");
	}
	return 0;
}