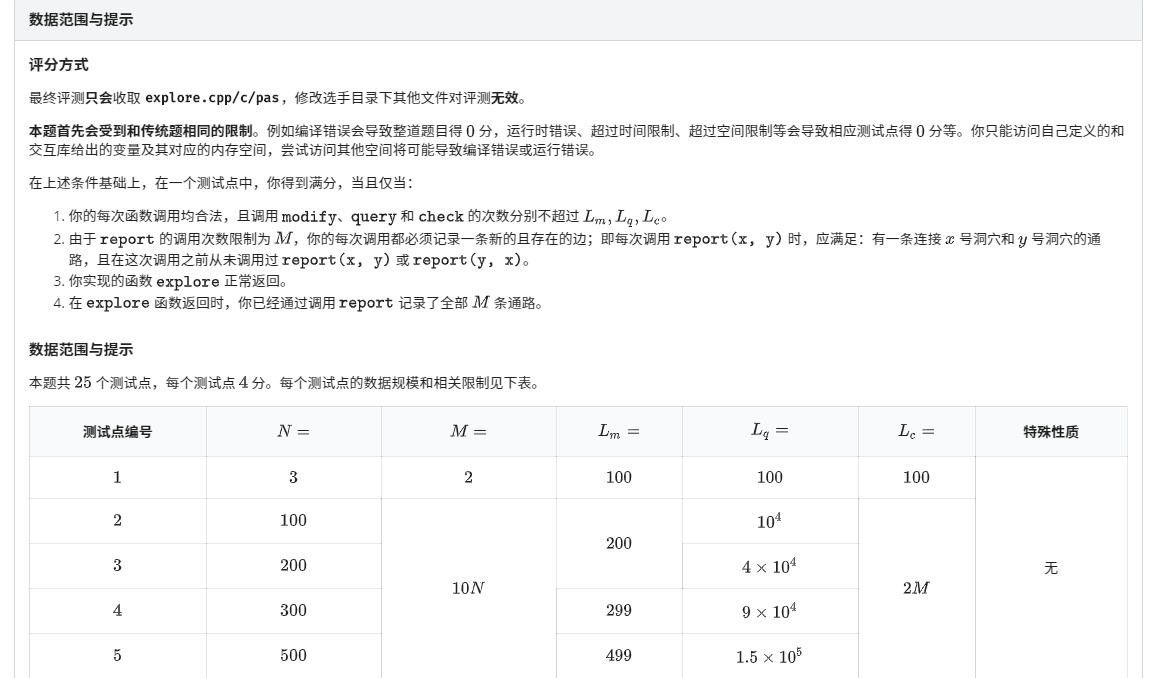
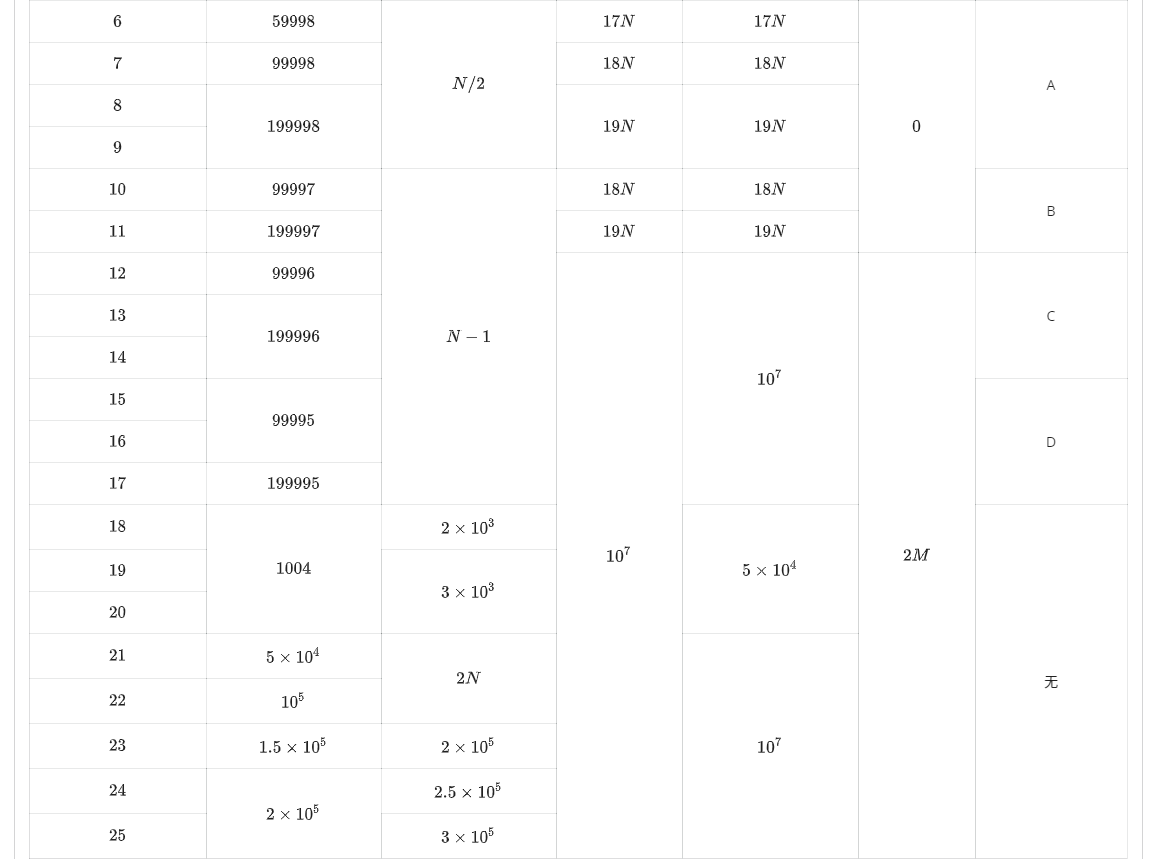
loj 3161 [NOI2019] 君的探险

loj 3161 [NOI2019] 君的探险

https://loj.ac/problem/3161

Tutorial

https://qaq-am.com/NOI2019-I%E5%90%9B%E7%9A%84%E6%8E%A2%E9%99%A9/

考虑B型数据,也就是图是一个父亲编号小于儿子的树的情况的做法.

考虑整体二分,对于当前区间([l,r]),维护父亲属于当前区间的集合(S),现在要将(S)分为父亲在([l,mid])中的和([mid+1,r])中的两类.

首先如果(x in [l,mid]),那么它的父亲一定在左区间.

考虑对于所有([l,mid])区间的节点调用modify,那么如果对于(x ot in [l,mid]),如果(x)洞穴的光源是亮的,说明它的父亲被修改了,也就说它的父亲在([l,mid])

就这样分治下去即可解决,询问次数(O(n log n))

考虑一般的数据,可以采用与B型数据类似的方法.每次随机一个排列对其执行这样的操作.此时在上面判断操作中,如果(x)亮了说明([l,mid])中有奇数个也就是至少一个点与之相邻,此时我们最后找到的是,每个点和排列中它前方某个点的连边,也就是一个与B型类似的树的结构.

注意储存已知的边并在判断是否有与([l,mid])区间的连边时排除已知边的影响.

一次操作完之后,用check函数找到所有已经找到所有邻边的点,之后不再对其计算.

Code

注意如果不是B型数据,那么从一开始就要随机排列,否则会被构造数据浪费(O(n log n))次查询后卡掉

对于(n le 500)的部分暴力计算.

#include "explore.h"
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#define debug(...) fprintf(stderr,__VA_ARGS__)
using namespace std;
const int maxn=2e5+50;
int cnt;
int a[maxn];
int head[maxn];
bool mark[maxn];
struct edge {
	int to,nex;
	edge(int to=0,int nex=0):to(to),nex(nex){}
};
vector<edge> G;
inline void addedge(int u,int v) {
	G.push_back(edge(v,head[u])),head[u]=G.size()-1;
	G.push_back(edge(u,head[v])),head[v]=G.size()-1;
}
namespace brute {
	int a[maxn];
	void sol(int n) {
		for(int i=0;i<n-1;++i) {
			modify(i);
			for(int j=i+1;j<n;++j) if(query(j)^a[j]) {
				a[j]^=1;
				report(i,j);
			}
		}
	}
}
inline void Report(int x,int y) {
	report(x,y),++cnt;
	addedge(x,y);
}
inline int Query(int x) {
	int re=query(x);
	for(int i=head[x];~i;i=G[i].nex) {
		int y=G[i].to;
		re^=mark[y];
	}
	return re;
}
void sol(int l,int r,vector<int> &v) {
	int n=v.size();
	if(l==r) {
		for(int i=0;i<n;++i) if(v[i]!=l) {
			Report(a[v[i]],a[l]);
		}
		return;
	}
	int mid=(l+r)>>1;
	vector<int> L,R;
	for(int i=l;i<=mid;++i) modify(a[i]),mark[a[i]]=1;
	for(int i=0;i<n;++i) {
		int x=v[i];
		if(x<=mid||Query(a[x])) L.push_back(x);
		else R.push_back(x);
	}
	for(int i=l;i<=mid;++i) modify(a[i]),mark[a[i]]=0;
	sol(l,mid,L),sol(mid+1,r,R);
}
void explore(int n,int m) {
	if(n<=500) {brute::sol(n); return;}
	memset(head,-1,sizeof(head));
	for(int i=0;i<n;++i) a[i]=i;
	if(n%10!=7) random_shuffle(a,a+n);
	do {
		vector<int> v;
		for(int i=0;i<n;++i) v.push_back(i);
		sol(0,n-1,v);
		if(cnt<m) {
			for(int i=0;i<n;++i) if(check(a[i])) {
				swap(a[i],a[--n]),--i;
			}
			random_shuffle(a,a+n);
		}
	} while(cnt<m);
}