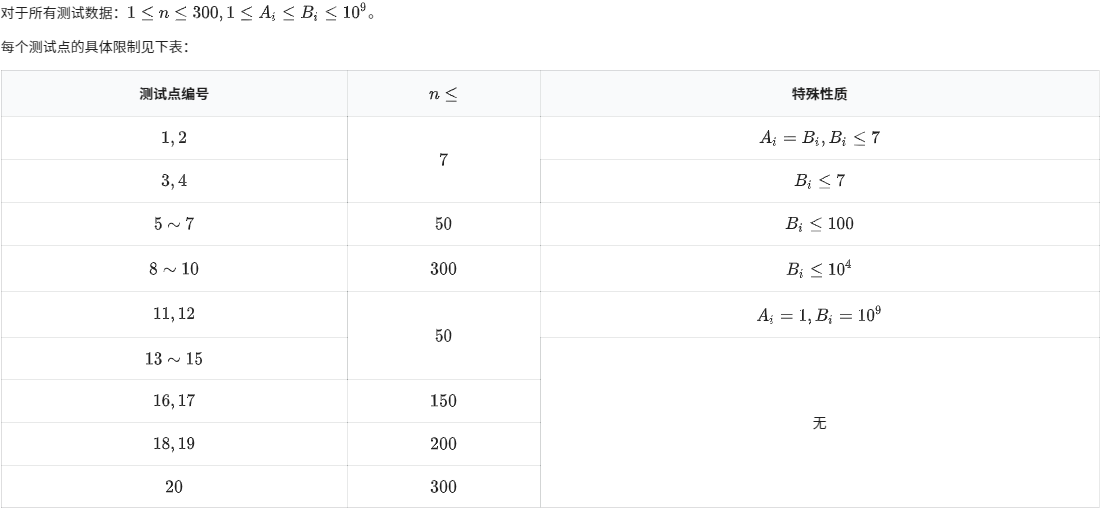
loj 3157 [NOI2019]机器人


Tutorial
https://blog.csdn.net/WAautomaton/article/details/96825203
http://yyy.is-programmer.com/posts/202122.html
https://www.cnblogs.com/suncongbo/p/11217236.html
https://www.cnblogs.com/Tiw-Air-OAO/p/13070992.html
考虑设 (dp(l,r,k)) 表示区间 ([l,r]) 中高度最大的柱子的高度为 (k) .
考虑枚举高度最大的柱子的位置 (k) ,需要满足 (|(k-l)-(r-k)| le 2) .
[dp(l,r,k)=sum_k(sum_{x le k} dp(l,k-1,x))(sum_{x<k}dp(k+1,r,x))
]
由于(k)对于位置的需求,所以需要计算的区间在(n=300)时只有(m=2220)个左右.
考虑若对于所有柱子有 (A_i=1,B_i=10^9) ,那么 (dp(l,l,k)=1) ,则它的前缀和可以看作关于 (k) 的一次函数,那么从上面的表达式可以看出, (dp(l,r,k))的前缀和就是关于(k)的(r-l+1)次多项式.
回到一般情况,此时的(dp(l,r,k))是一个分段函数,我们可以根据(A_i,B_i+1)将高度分为若干段,满足每一段对于每个柱子的合法性不变.设当前段为([L,R)),此时可以将(dp(l,r,k))看作关于(k-L)的函数,而常数项则是(dp(l,r,L-1)).
那么我们DP维护点值,利用拉格朗日插值进行转移即可.计算一段的时间复杂度为 (O(mn^2)) .总复杂度 (O(mn^3)) .但是由于常数很优秀,所以可以通过
Code
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define inver(a) power(a,mod-2)
using namespace std;
inline char gc() {
static char buf[100000],*l=buf,*r=buf;
return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void rd(T &x) {
x=0; int f=1,ch=gc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=gc();}
x*=f;
}
typedef long long ll;
const int mod=1e9+7;
const int maxn=300+5,maxm=2300;
const int maxp=maxn<<1;
int n,A[maxn],B[maxn];
int fac[maxn],inv[maxn];
int p,H[maxp];
int ncnt,id[maxn][maxn];
int c[maxm],good[maxn];
int dp[maxm][maxn],cnt[maxm],deg[maxm],vis[maxm];
inline int add(int x) {return x>=mod?x-mod:x;}
inline int sub(int x) {return x<0?x+mod:x;}
ll power(ll x,ll y) {
ll re=1;
while(y) {
if(y&1) re=re*x%mod;
x=x*x%mod;
y>>=1;
}
return re;
}
int cal(int n,int x,int *y) {
static int pre[maxn],suf[maxn];
pre[0]=x;
for(int i=1;i<=n;++i) pre[i]=(ll)pre[i-1]*sub(x-i)%mod;
suf[n]=sub(x-n);
for(int i=n-1;i>=0;--i) suf[i]=(ll)suf[i+1]*sub(x-i)%mod;
int re=0;
for(int i=0;i<=n;++i) {
int d=(ll)((n-i)&1?mod-1:1)*inv[n-i]%mod*inv[i]%mod;
if(i!=0) d=(ll)d*pre[i-1]%mod;
if(i!=n) d=(ll)d*suf[i+1]%mod;
re=(re+(ll)d*y[i])%mod;
}
return re;
}
void extend(int u,int d) {
while(cnt[u]<d) {
++cnt[u];
dp[u][cnt[u]]=cal(deg[u],cnt[u],dp[u]);
}
}
void dfs_init(int l,int r) {
if(id[l][r]!=-1) return;
if(l>r) {id[l][r]=0; return;}
id[l][r]=++ncnt;
for(int k=l;k<=r;++k) if(abs((k-l)-(r-k))<=2) {
dfs_init(l,k-1),dfs_init(k+1,r);
}
}
int dfs(int l,int r) {
int u=id[l][r]; if(vis[u]) return u; vis[u]=1;
cnt[u]=deg[u]=0;
for(int k=l;k<=r;++k) if(abs((k-l)-(r-k))<=2) {
int L=dfs(l,k-1),R=dfs(k+1,r); if(!good[k]) continue;
int d=max(deg[u],deg[L]+deg[R]);
extend(L,d+1),extend(R,d),extend(u,d);
for(int i=0;i<=d;++i) dp[u][i]=(dp[u][i]+(ll)dp[L][i+1]*dp[R][i])%mod;
deg[u]=d;
}
if(deg[u]==0&&dp[u][0]==0) dp[u][0]=c[u];
else {
for(int i=deg[u];i>=0;--i) dp[u][i+1]=dp[u][i];
dp[u][0]=c[u],++deg[u],++cnt[u];
for(int i=1;i<=deg[u];++i) dp[u][i]=add(dp[u][i]+dp[u][i-1]);
}
return u;
}
void init(int n) {
fac[0]=1;
for(int i=1;i<=n;++i) fac[i]=(ll)fac[i-1]*i%mod;
inv[n]=inver(fac[n]);
for(int i=n;i>=1;--i) inv[i-1]=(ll)inv[i]*i%mod;
}
int main() {
freopen("robot.in","r",stdin);
freopen("robot.out","w",stdout);
rd(n);
init(n);
for(int i=1;i<=n;++i) {
rd(A[i]),rd(B[i]),++B[i];
H[++p]=A[i],H[++p]=B[i];
}
sort(H+1,H+p+1),p=unique(H+1,H+p+1)-H-1;
for(int i=1;i<=n;++i) {
A[i]=lower_bound(H+1,H+p+1,A[i])-H;
B[i]=lower_bound(H+1,H+p+1,B[i])-H;
}
memset(id,-1,sizeof(id));
dfs_init(1,n),c[0]=1;
for(int i=1;i<p;++i) {
for(int j=1;j<=n;++j) good[j]=A[j]<=i&&i<B[j];
dfs(1,n);
for(int j=1;j<=ncnt;++j) {
vis[j]=0;
c[j]=cal(deg[j],H[i+1]-H[i],dp[j]);
for(int k=0;k<=cnt[j];++k) dp[j][k]=0;
}
}
printf("%d
",c[1]);
return 0;
}