一、聚类性能度量
通常我们希望聚类结果的“簇内相似度”(intra-cluster similarity)高且“簇间相似度”(inter-cluster similarity)低。聚类性能度量大致有两类:一类是将聚类结果与某个“参考模型”(reference model)进行比较,称为“外部指标”(external index);另一类是直接考查聚类结果而不利用任何参考模型。称为“内部指标”(internal index)
外部指标:
假定C是聚类给出的簇划分,C*是参考模型给出的簇划分,$lambda$ 与 $lambda^*$分别表示C和C*对应的簇标记向量。
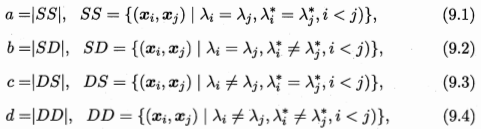
基于上式导出常用的聚类性能度量外部指标:
1. Jaccard系数(Jaccard Coefficient,JC)
2. FM指数(Fowlkes and Mallows Index,FMI)
上述三值均在[0,1]区间,值越大越好
内部指标:

簇C内样本间的平均距离:
簇C内样本间最远距离:
簇Ci与Cj最近样本间的距离
簇Ci与Cj中心点间的距离:
基于上式可导出常用的聚类性能度量内部指标:
1. DB指数(Davies-Bouldin Index,DBI)
类比簇间相似度
2. Dunn指数(Dunn Index,DI)
类比簇内相似度
DBI的值越小越好,DI相反,越大越好
二、距离计算
最常用的是“闵可夫斯基距离”(Minkowski distance)
p=2时,闵可夫斯基距离即欧氏距离(Euclidean distance)
p=1时,闵可夫斯基距离即曼哈顿距离(Manhattan distance)
我们常将属性划分为“连续属性”(continuous attribute)(数值属性)和“离散属性”(categorical attribute)(列名属性)。但在讨论距离计算时,属性上是否定义了“序”关系更为重要。能直接在属性值上计算距离的称为“有序属性”,不能直接在属性值上计算距离的称为“无序属性”(大多数类别特征)。显然,闵可夫斯基距离可用于有序属性。
对无序属性可采用VDM(Value Difference Metric)。令Mu,a表示在属性u上取值为a的样本数,Mu,a,i表示在第i个样本簇中在属性u上取值为a的样本数,k为样本簇数,则属性u上两个离散值a与b之间的VDM距离为:
将闵可夫斯基距离和VDM结合可处理混合属性。不失一般性,令有序属性排列在无序属性之前,则
当样本空间中不同属性的重要性不同时,可使用“加权距离”,以加权闵可夫斯基距离为例:通常权值之和为1。
三、原型聚类
k-means算法
给定样本集D={x1,x2,…,xm},“k均值”(k-means)算法针对聚类所得簇划分C={C1,C2,…,Ck}最小化平方误差
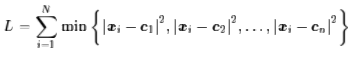

最小化式(9.24)并不容易,找到它的最优解需考察样本集D所有可能的簇划分,这是一个NP难问题。k均值算法采用了贪心策略,通过迭代优化来近似求解式。以下是k均值算法描述

kmeans缺点:1、需先确定k的个数 2、对噪声和离群点敏感 3、结果不一定是全局最优,只能保证局部最优
如何初始化簇中心:http://blog.csdn.net/shennongzhaizhu/article/details/51871891
K个初始类簇点的选取除了随机选取之外还有两种方法:1)选择彼此距离尽可能远的K个点 2)先对数据用层次聚类算法或者Canopy算法进行聚类,得到K个簇之后,从每个类簇中选择一个点,该点可以是该类簇的中心点,或者是距离类簇中心点最近的那个点。
1) 选择彼此距离尽可能远的K个点
首先随机选择一个点作为第一个初始类簇中心点,然后选择距离该点最远的那个点作为第二个初始类簇中心点,然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点,以此类推,直至选出K个初始类簇中心点。
2) 选用层次聚类或者Canopy算法进行初始聚类,然后利用这些簇的中心点作为KMeans算法初始簇中心点。
K值的确定
给定一个合适的簇指标,比如平均半径或直径,只要我们假设的簇的数目等于或者高于真实的簇的数目时,该指标上升会很缓慢,而一旦试图得到少于真实数目的簇时,该指标会急剧上升。
类簇的直径是指类簇内任意两点之间的最大距离。
类簇的半径是指类簇内所有点到类簇中心距离的最大值。
kmeans实现:
def loadDataSet(fileName): dataMat = [] fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split(' ') fltLine = map(float, curLine) dataMat.append(fltLine) return dataMat #计算两个向量的距离,用的是欧几里得距离 def distEclud(vecA, vecB): return sqrt(sum(power(vecA - vecB, 2))) #随机生成初始的质心(ng的课说的初始方式是随机选K个点) def randCent(dataSet, k): n = shape(dataSet)[1] centroids = mat(zeros((k,n))) for j in range(n): minJ = min(dataSet[:,j]) rangeJ = float(max(array(dataSet)[:,j]) - minJ) centroids[:,j] = minJ + rangeJ * random.rand(k,1) return centroids def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent): m = shape(dataSet)[0] clusterAssment = mat(zeros((m,2)))#create mat to assign data points #to a centroid, also holds SE of each point centroids = createCent(dataSet, k) clusterChanged = True while clusterChanged: clusterChanged = False for i in range(m):#for each data point assign it to the closest centroid minDist = inf minIndex = -1 for j in range(k): distJI = distMeas(centroids[j,:],dataSet[i,:]) if distJI < minDist: minDist = distJI; minIndex = j if clusterAssment[i,0] != minIndex: clusterChanged = True clusterAssment[i,:] = minIndex,minDist**2 print centroids for cent in range(k):#recalculate centroids ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean return centroids, clusterAssment
学习向量量化(LVQ)
与k均值算法类似,“学习向量量化”(Learning Vector Quantization,LVQ)也是试图找到一组原型向量来刻画聚类结构,LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
样本$x_i$是n维向量,每个原型向量也是n维向量,每个原型向量代表一个聚类簇。
LVQ算法描述如下:

首先对原型向量进行初始化,然后对原型向量进行迭代优化,在每一轮迭代中,算法随机选取一个有标记训练样本,找出与其距离最近的原型向量,并根据两者的类别标记是否一致来对原型向量进行更新。LVQ的关键是第6-10行的更新原型向量,对样本Xj,若最近的原型向量pi与Xj的类别标记相同,则令pi向Xj的方向靠。若标签不同,则远离Xj。
在学得一组原型向量后,即可实现对样本空间X的簇划分。对任意样本x,它将被划入于其距离最近的原型向量所代表的簇中
高斯混合聚类
与k均值、LVQ用原型向量来刻画聚类结构不同,高斯混合聚类采用概率模型来表达聚类原型。
高斯分布的定义:对n维样本空间X中的随机向量x,若x服从高斯分布,其概率密度函数为
高斯分布完全由均值向量和协方差矩阵这两个参数确定。
根据概率密度函数可定义高斯混合分布:
该分布共由k个混合成分组成,每个混合成分对应一个高斯分布。假设样本的生成过程由高斯混合分布给出。令随机变量Zj∈{1,2,…,k}表示生成样本Xj的高斯混合成分,根据贝叶斯定理,Zj的后验分布对应于:
换言之,PM(Zj=i|Xj)给出了样本Xj由第i个高斯混合成分生成的后验概率,为方便叙述,将其简记为γji(i=1,2,…,k)。当高斯混合分布(9.29)已知时,高斯混合聚类将把样本集D划分为k个簇C={C1,C2,…,Ck},每个样本Xj的簇标记λj如下确定:
即将样本划分进后验概率最大的那个高斯混合成分。因此,从原型聚类的角度来看,高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画,簇划分则由原型对应后验概率确定。对于式(9.29)模型参数{(αi,μi,Σi)|1≤i≤k}如何求解呢?可以采用极大似然估计,即最大化(对数)似然

LL(D)是对数似然的期望值。上式常采用EM算法进行迭代优化求解。EM算法步骤在此简要复习一下:
EM(Expectation-Maximization)算法是常用的估计参数隐变量(隐变量:未观测变量的学名)的利器,它是一种迭代式地方法,基本思想是:若参数θ已知,则可根据训练数据推断出最优隐变量Z的值(E步);反之,若Z的值已知,则可方便地对参数θ做极大似然估计(M步)。EM算法可看作是一种非梯度优化方法(坐标下降法)。
简要来说,EM算法使用E步和M步交替计算:
E步(期望E步):利用当前估计的参数计算对数似然的期望值
M步(最大化M步):寻找能使E步产生的似然期望最大化的参数值
重复E步、M步直至收敛。
根据上述的EM算法步骤可得高斯混合模型的EM算法:在每步迭代中,先根据当前参数来计算每个样本属于每个高斯成分的后验概率(E步),再根据更新公式更新模型参数,包括均值向量、协方差矩阵以及新混合系数。具体高斯混合聚类算法步骤如下:
四、层次聚类
层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略,也可采用“自顶向下”的分拆策略。
AGNES是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数,这里的关键是如何计算聚类簇之间的距离。可根据如下式子计算距离:
显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定,而平均距离则有两个簇的所有样本共同决定。当聚类簇距离分别由这三个距离计算时,AGNES算法被相应地称为“单链接”(single-linkage)、“全链接”(complete-linkage)或“均链接”(average-linkage)算法。AGNES算法描述如下:
参考:
http://bealin.github.io/2017/02/27/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E7%B3%BB%E5%88%97%E2%80%9410-%E8%81%9A%E7%B1%BB/
