1、交叉熵的来源
一条信息的信息量大小和它的不确定性有很大的关系,不确定性越大,则信息量越大。一句话如果需要很多外部信息才能确定,我们就称这句话的信息量比较大。比如你听到“云南西双版纳下雪了”,那你需要去看天气预报、问当地人等等查证(因为云南西双版纳从没下过雪)。相反,如果和你说“人一天要吃三顿饭”,那这条信息的信息量就很小,因为这条信息的确定性很高。
将事件$x_0$的信息量定义如下(其中p($x_0$)表示事件$x_0$发生的概率):
![]()
熵是表示随机变量不确定性的度量,是对所有可能发生的事件产生的信息量的期望。公式如下:
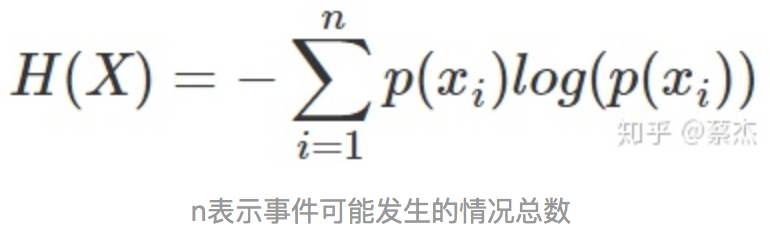
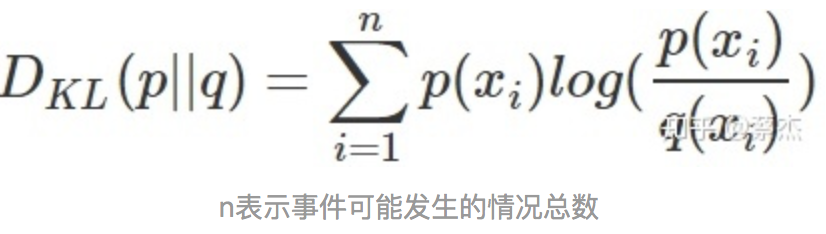
KL散度的值越小表示两个分布越接近。
我们将KL散度的公式进行变形,得到: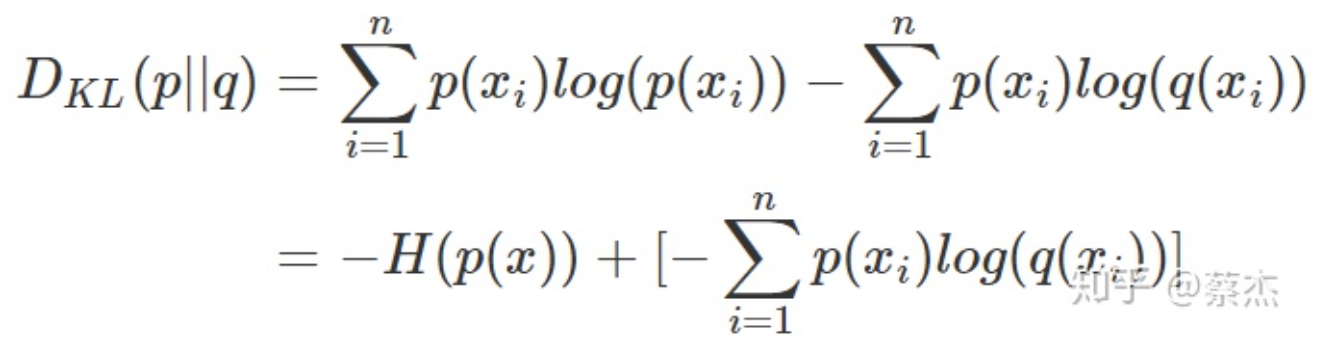

对于输入的,其对应的类标签为
,我们的目标是找到这样的
使得
最大。在二分类的问题中,我们有:
其中,是模型预测的概率值,
是样本对应的类标签。
将问题泛化为更一般的情况,多分类问题:
由于连乘可能导致最终结果接近0的问题,一般对似然函数取对数的负数,变成最小化对数似然函数。
![]()
从MSE loss可以看出, MSE无差别得关注全部类别上预测概率和真实概率的差,交叉熵损失关注的是正确类别的预测概率,而我们最终目标是获得正确的类别.
3、Softmax交叉熵损失函数
【https://www.jianshu.com/p/1536f98c659c,https://zhuanlan.zhihu.com/p/27223959 】
指数形式的原因:如果使用max函数,虽然能完美的进行分类但函数不可微从而无法进行训练,引入以 e 为底的指数并加权归一化,一方面指数函数使得结果将分类概率拉开了距离,另一方面函数可微。
softmax函数求导:
对每个样本,它属于类别的概率为:
对softmax函数进行求导,即求
第项的输出对第
项输入的偏导。
代入softmax函数表达式,可以得到:
用我们高中就知道的求导规则:对于
它的导数为
所以在我们这个例子中,
上面两个式子只是代表直接进行替换,而非真的等式。
(即
)对
进行求导,要分情况讨论:
- 如果
,则求导结果为
- 如果
,则求导结果为
再来看对
求导,结果为
。
所以,当时:
当时:
其中,为了方便,令
softmax的计算与数值稳定性:
在Python中,softmax函数为:
def softmax(x):
exp_x = np.exp(x)
return exp_x / np.sum(exp_x)
一种简单有效避免该问题的方法就是让exp(x)中的x值不要那么大或那么小,在softmax函数的分式上下分别乘以一个非零常数:
这里是个常数,所以可以令它等于
。加上常数
之后,等式与原来还是相等的,所以我们可以考虑怎么选取常数
。我们的想法是让所有的输入在0附近,这样
的值不会太大,所以可以让
的值为:
这样子将所有的输入平移到0附近(当然需要假设所有输入之间的数值上较为接近),同时,除了最大值,其他输入值都被平移成负数,为底的指数函数,越小越接近0,这种方式比得到nan的结果更好。