dp算法之硬币找零问题

题目：硬币找零

题目介绍：现在有面值1、3、5元三种硬币无限个，问组成n元的硬币的最小数目？

分析：现在假设n=10，画出状态分布图：

硬币编号	硬币面值p
1	1
2	3
3	5

编号i/n总数j	0	1	2	3	4	5	6	7	8	9	10
1	0	1	2	3	4	5	6	7	8	9	10
2	0	1	2	1	2	3	2	3	4	3	4
3	0	1	2	1	2	1	2	3	2	3	2

设所需硬币最小数目为m，则可以看出m[ i ][  j ]=m[ i-1 ][  j-k*p[ i ]] + k.其中k*p[ i ]<=j.确切的说，k=j/p[ i ].

dp算法的显著特征之一就是具有最优子结构，且这一状态的最优解与上一状态的最优解有关。写出状态方程之后我们就可以开始具体处理代码了。

#include <iostream>
using namespace std;
int main()
{
    int i, j, k;
    int m, n;//m就是总值
    cout << "总数：" << endl;
    cin >> m;
    //m = 10, ;
    n = 3;
    int **c = new int *[n + 1];
    for (i = 0; i <= n; i++)
    {
        c[i] = new int[m + 1];
    }
    int p[4] = { 0,1,3,5 };
    for (i = 0; i <= n; i++)
    {
        for (j = 0; j <= m; j++)
        {
            c[i][j] = 0;//初始化
        }
    }
    for (i = 1; i <= n; i++)
    {
        for (j = 1; j <= m; j++)
        {
            k = j / p[i];
            c[i][j] = c[i - 1][j - k * p[i]] + k;
        }
    }
    for (i = 1; i <= n; i++)
    {
        for (j = 0; j <= m; j++)
        {
            cout << c[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

分析：这个硬币找零问题在dp算法中比较经典，复杂度低于经典的背包问题，因为背包问题还要考虑 k 的值，需要遍历 k 的值来找到一个最优解，此题不需要。

结果：

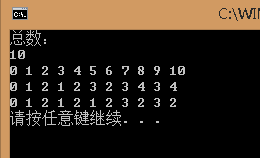
下一篇将要分析经典的背包问题了，包括01背包、完全背包、多重背包。