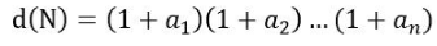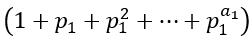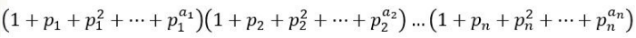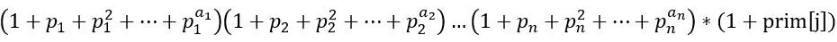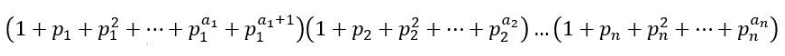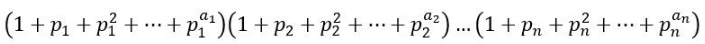整数惟一分解定理的推论
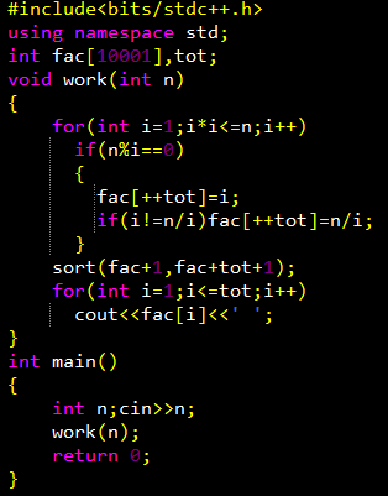
1、求N的正约数集合
因为约数总是成对出现的(除了完全平方数)。因此只需扫描1~sqrt(N)之间的数就能得到N的正约数集合。
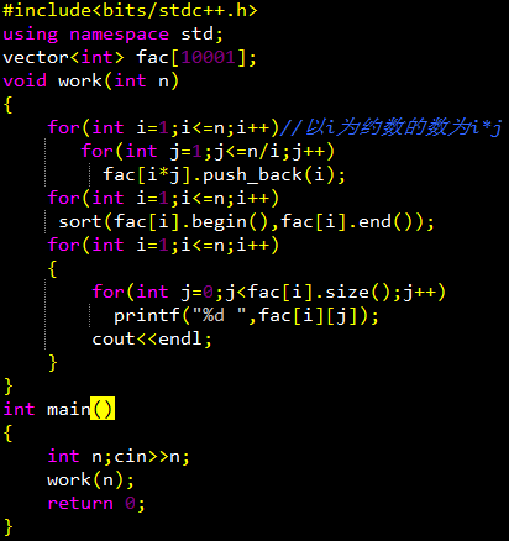
2、求1~N的每个数的正约数集合
3、约数个数
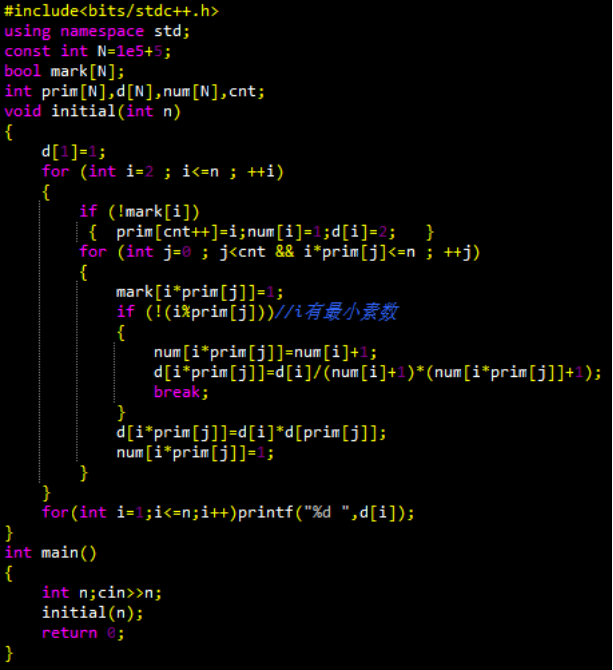
算术基本定理中,根据拆分后的素因子的指数,我们可以求出每个 N 的约数的个数。
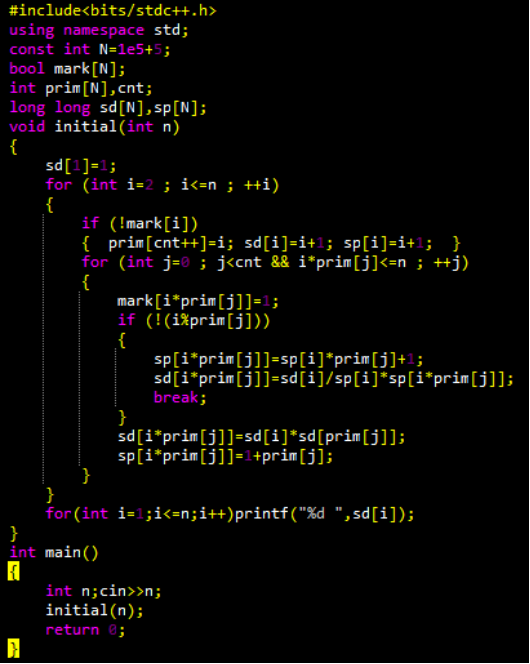
根据这个式子,我们可以用线性筛去筛出当前 1~N 的约数个数。筛的过程中,我们需要保存下最小素因子的个数。
下面推导中
-
d(i) 表示 i 的约数个数
-
num[i] 表示 i 的最小素因子的个数
-
prim[i] 表示 第 i 个素数
① 当前数N是素数
这种情况我们很容易得到,当前的 d(N) = (1+1) = 2, 因为素数只有一个素因子(就是它本身),并且指数为 1 。 而最小素因子个数 num[N] = 1
② i%prim[j] !=0
这种情况,i 当中,并不包含 prim[j] 这个素因子,然而,i*prim[j] 中, 包含了一个 prim[j]我们可以从前面得到 i 的所有约数个数 然后在补上 当前多了 素因子 prim[j] 的个数所以最后 d(i*prim[j]) = d(i)*d(prim[j])而且由于 当前的 prim[j] 必然是 i*prim[j] 的最小素因子 (因为从小到大枚举啊!), 我们要记录下这个最小素因子的个数所以保存一个个数 num[i*prim[j]] = 1
③ i%prim[j]==0
这种情况, i 中必然包含了至少 1 个 prim[j] ,而且 prim[j] 也必定是 i 的最小素因子,因为每次枚举都是从小的素数开始枚举。
而 i*prim[j] 比起 i 则是多了一个最小素因子个数,即 1+a1
那么 i*prim[j] 的约数个数 应该是 (1+a1+1)(1+a2)…(1+an)
之后,我们就要用到我们之前记录下的最小素因子个数了,因为我们可以知道 i 的最小素因子个数 为 num[i] ,而 d(i) 中 已经包含了(1+a1)(1+a2)…(1+an) 这时我们 我们可以除去第一项1+a1 然后乘以 1+a1+1 ,就可以得到 d(i*prim[j]) 的约数个数了。
d(i*prim[j]) = d(i) / (num[i]+1) * (num[i]+2)
当前 num[i*prim[j]] = num[i]+1 ,继续保存下当前最小素因子个数。
↓↓↓用线性筛打表出 1 到 N 的数的约数个数。
4、约数和
算数基本定理中,如果要求N的约数的和,可以用这条式子。
同样,我们一样可以用这条式子去筛出当前 N 的约数和。 筛的过程中,我们需要保存最小素因子的那一项的和,即
下面推导中
-
sd(i) 表示 i 的约数和
-
sp[i] 表示 i 的最小素因子的等比数列的和 (上面说要保存的那一项)
-
prim[i] 表示第 i 个素数
①当前数N是素数
这种情况我们可以很容易得到,当前的 sd(N) = 1+i
因为素数只有一个素因子,即只有一项合式,且指数最高为 1 。
而该项 sp[N] = 1+i
② i%prim[j] !=0
这种情况,i 当中,并不包含 prim[j] 这个素因子,然而,i*prim[j] 中, 包含了一个 prim[j]而前面我们已经得到了 i 的约数和了,而其中不包括 (1+prim[j]) 这一项,而 i*prim[j] 的约数和只是多了这一项。
i 的约数和是
那么 i*prim[j] 的最后结果应该是
即 sd(i*prim[j]) = sd(i) * sd(prim[j])
而 prim[j] 是 i*prim[j] 的最小素因子 (因为从小到大枚举),因此sp[i*prim[j]] = 1+prim[j]
③ i%prim[j]==0
这种情况, i 中必然包含了至少 1 个 prim[j] ,而且 prim[j] 也必定是 i 的最小素因子,因为每次枚举都是从小的素数开始枚举。
只不过 i*prim[j] 比起 i 则是在最小素因子那一项多了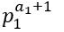
那么 i*prim[j] 的约数和就是
之后,我们用到前面保存下来的最小素因子那一项的和,因为 i 中 应该是
我们可以知道最小素因子的那一项的和,而要得到
只需要将第一项 乘以 prim[j] 然后再 加一,就可以得到了。
sd(i*prim[j]) = sd(i) / sp[i] * (sp[i]*prim[j]+1)
当前 sp[i*prim[j]] = sp[i]*prim[j]+1,继续保存最小素因子一项的和。
用线性筛打表出 1 到 N 的约数和。
5、最大公约数
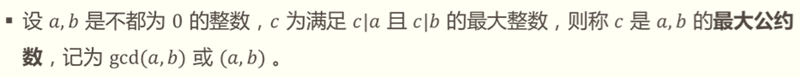
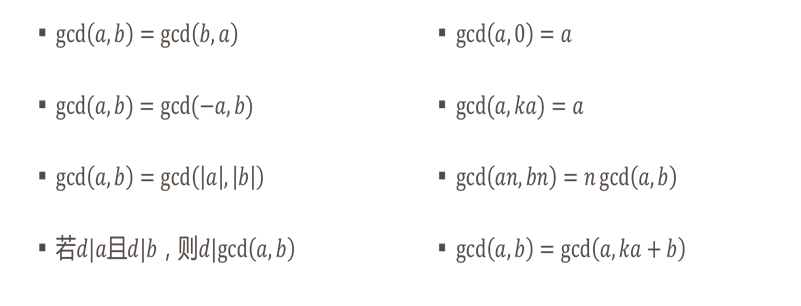
①计算gcd(a,b):枚举法

②计算gcd(a,b):素因数分解法
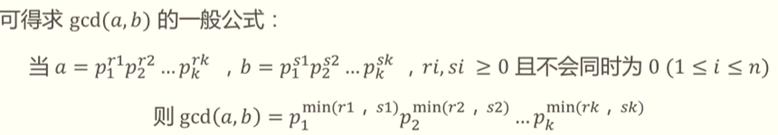

③计算gcd(a,b):欧几里得法(又称“辗转相除法”)

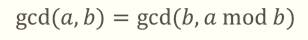

④计算gcd(a,b):适用于高精度的二进制法(又称“更相减损术”)


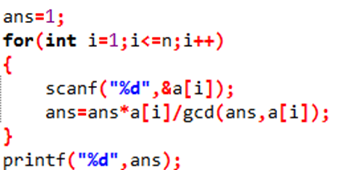
6、最小公倍数