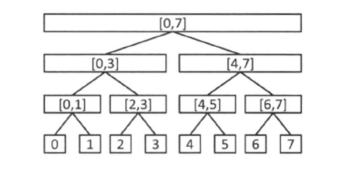
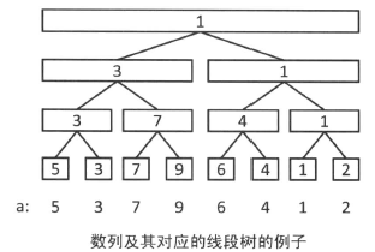
线段树上每个节点维护了它所对应的区间的最小值。我们可以用简单的递归来得到这棵初始线段树,即用build(k,l,r)来表示当前要构建区间[l,r]的线段树,k表示区间[l,r]所对应的标号,若l=r则我们可以直接构建一个叶节点,它的区间最小值就是al;否则我们新建一个节点,它的两个子节点可以通过build(k*2,l,mid)与build(k*2+1,mid+1,r)来递归得到,它的区间最小值就是两个儿子的区间最小值中的较小者。因为节点个数是n*2级别的,所以这个过程是O(n)级别的。
需要特别注意的是,用上述标号方法,线段树的数组要开到4*n级别。
【代码实现】
void build(int k,int l,int r) //k表示当前节点的编号,l,r为当前节点所代表 { 的区间
if(l==r) //当前节点为叶子节点
{
mi[k]=a[l]; //对应区间的最小值为原序列中的对应值
return;
}
int mid=(l+r)/2;
build (k*2,l,mid); //构造左子树
build (k*2+1,mid+1,r); //构造右子树
mi[k]=min(mi[k*2],mi[k*2+1]); //自下向上更新
}
单点修改操作
举个栗子:如下图
假设要将a0修改为2,那么我们只需要重新计算下图所示的4个节点信息:

【代码实现】
void change(int k,int l,int r,int x,int v) //x为原序列的位置,v为要改为的值
{
if(l==r&&l==x) //当前节点为对应的叶子节点
{ mi[k]=v; return; } //修改叶子节点
int mid=(l+r)/2;
if(x<=mid) change(k*2,l,mid,x,v); //修改左子区间
if(x>mid) change(k*2+1,mid+1,r,x,v); //修改右子区间
mi[k]=min(mi[k*2],mi[k*2+1]); //更新相关的值
}
区间询问操作
若要询问区间[0,6],我们只需要用到下图中的三个节点的信息:
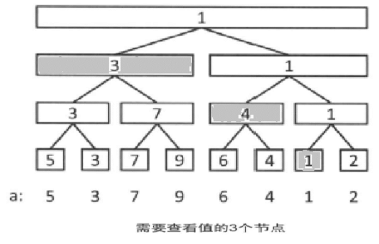
考虑怎样提取这些区间。我们可以递归处理这个求解过程:初始时访问根节点。接下来当前访问节点所对应区间与询问区间的关系有三种情况:
(1)当前区间与询问区间完全无交集,那么此时可以直接返回一个不影响答案的极大值,不继续递归(因为子节点肯定也与询问区间无交集)。
(2)询问区间完全包含当前区间,那么直接返回当前节点所维护的区间最小值(因为这段区间的信息都在这个节点维护好了,不需要递归下去求解)。
(3)除了上面两种情况,我们对两个儿子递归处理,返回两个结果中的较小值。
【代码实现】
int query_min(int k,int l,int r,int x,int y)
//k当前节点,x,y为询问区间,l,r为当前节点维护区间
{
if(y<l||x>r) return 2147483647;//若与询问区间完全无交集,返回一个极大值
if(x<=l&&r<=y) return mi[k]; //询问区间在当前区间,返回维护好的最小值
int mid=(l+r)/2;
return min(query_min(k*2,l,mid),query_min(k*2+1,mid+1,r));
//否则分别处理左子区间和右子区间
}
小试牛刀——
1547:【 例 1】区间和
【题目描述】
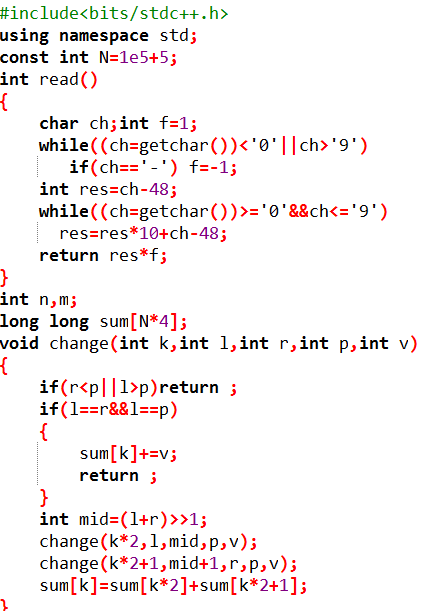
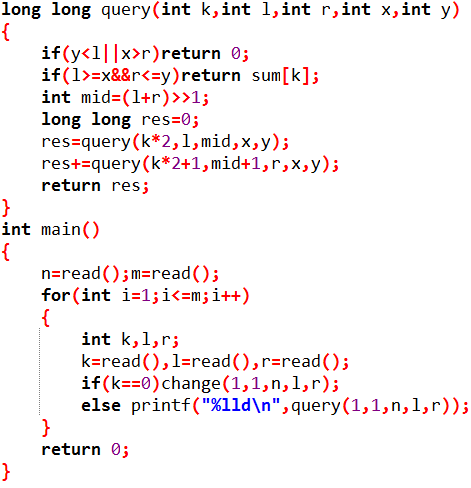
给定一个全0数列,规定有两种操作,一是修改某个元素,二是求区间的连续和。
【输入】
输入数据第一行包含两个正整数n,m(n≤100000,m≤500000)以下是m行, 每行有三个正整数k,a,b (k=0或1,a,b≤n).k=0时表示将a处数字加上b,k=1时表示询问区间[a,b]内所有数的和。
【输出】
对于每个询问输出对应的答案。
【输入样例】
10 20 0 1 10 1 1 4 0 6 6 1 4 10 1 8 9 1 4 9 0 10 2 1 1 8 0 2 10 1 3 9 0 7 8 0 3 10 0 1 1 1 3 8 1 6 9 0 5 5 1 1 8 0 4 2 1 2 8 0 1 1
---->(乱入:格式不太对请多见谅(o´ω`o)ノ)
【输出样例】
10 6 0 6 16 6 24 14 50 41
热腾腾的代码来啦!(σ゚∀゚)σ..:*☆哎哟不错哦