在真实的世界中,缺失数据是经常出现的,并可能对分析的结果造成影响。我们需要了解数据缺失的原因和数据缺失的类型,并从数据中识别缺失值,探索数据缺失的模式,进而处理缺失的数据。本文概述处理数据缺失的方法。
一,数据缺失的原因
首先我们应该知道:数据为什么缺失?数据的缺失是我们无法避免的,可能的原因有很多种,博主总结有以下三大类:
- 无意的:信息被遗漏,比如由于工作人员的疏忽,忘记而缺失;或者由于数据采集器等故障等原因造成的缺失,比如系统实时性要求较高的时候,机器来不及判断和决策而造成缺失;
- 有意的:有些数据集在特征描述中会规定将缺失值也作为一种特征值,这时候缺失值就可以看作是一种特殊的特征值;
- 不存在:有些特征属性根本就是不存在的,比如一个未婚者的配偶名字就没法填写,再如一个孩子的收入状况也无法填写;
总而言之,对于造成缺失值的原因,我们需要明确:是因为疏忽或遗漏无意而造成的,还是说故意造成的,或者说根本不存在。只有知道了它的来源,我们才能对症下药,做相应的处理。
二,数据缺失的类型
在对缺失数据进行处理前,了解数据缺失的机制和形式是十分必要的。将数据集中不含缺失值的变量称为完全变量,数据集中含有缺失值的变量称为不完全变量。而从缺失的分布来将缺失可以分为完全随机缺失,随机缺失和完全非随机缺失。
缺失数据主要分为以下三类:
- 完全随机缺失(missing completely at random,MCAR):数据的缺失是完全随机的,不依赖于其他变量,跟其他变量不相关,不影响样本的无偏性,如家庭地址缺失;
- 随机缺失(missing at random,MAR):数据的缺失不是完全随机的,依赖于其他完全变量,如财务数据缺失情况与企业的大小有关;
- 非随机缺失(missing not at random,MNAR):数据的缺失与不完全变量的取值有关,如高收入人群不原意提供家庭收入;
对于随机缺失和非随机缺失,直接删除记录是不合适的,上面的定义已经给出原因。随机缺失可以通过已知变量对缺失值进行估计,而非随机缺失的非随机性还没有很好的解决办法。而对于完全随机缺失可以直接删除。
三,识别缺失值
Python使用NnN代表缺失值,NaN(不是一个数)代表不可能的值,符号Inf和-Inf分别代表正无穷和负无穷。
判断一个数据集是否存在缺失数据,通常从两个方面入手,
- 一个是变量的角度,即判断每个变量中是否包含缺失值;
- 另一个是数据行的角度,即判断每行数据中是否包含缺失值。
在Python环境中,可以使用DataFrame对象的isnull()方法来判断缺失值,isnull()方法返回与原数据集的shape相同的矩阵,矩阵的元素是bool类型的值,可以称作原始数据集的影子矩阵,如果影子矩阵的元素值是1,表示在原始数据集中对应该位置的值是缺失的,如果影子矩阵元素的值是0,表示在原始数据集中对应该位置的值是有效的。下面使用isnull()方法对df数据进行判断,统计输出的结果如下表所示。
# 判断各变量中是否存在缺失值 df.isnull().any(axis = 0) # 各变量中缺失值的数量 df.isnull().sum(axis = 0) # 各变量中缺失值的比例 df.isnull().sum(axis = 0)/df.shape[0]

如上结果所示,数据集df中有三个变量存在缺失值,即gender、age和edu,它们的缺失数量分别为136、100和1,927,缺失比例分别为4.53%、3.33%和64.23%。
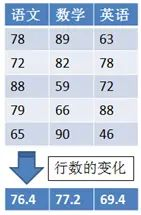
读者可能对代码中的“axis=0”感到困惑,下面通过图表的形式来说明axis参数的用法:
假设上图为学生的考试成绩表,axis=0表示按学科分别计算每个学科的平均分,就是上图中从上到下的转换。
axis=1 表示按学生分别计算每个学生的总分,将是上图从左到右的转换。
1,判断每列是否存在缺失值
为了得到每一列的判断结果,需要any()方法(且设置方法内的axis参数为0);
# 判断各变量中是否存在缺失值 df.isnull().any(axis = 0)
2,识别数据行的缺失值分布情况
统计各变量的缺失值个数可以在isnull()的基础上使用sum()方法(同样需要设置axis参数为0);计算缺失比例就是在缺失数量的基础上除以总的样本量(shape方法返回数据集的行数和列数,[0]表示取出对应的数据行数)。代码如下:
# 缺失观测的行数 df.isnull().any(axis = 1).sum() # 缺失观测的比例 df.isnull().any(axis = 1).sum()/df.shape[0]
代码中使用了两次any“方法”,第一次用于判断每一行对应的True(即行内有缺失值)或False值(即行内没有缺失值);第二次则用于综合判断所有数据行中是否包含缺失值。同理,进一步还可以判断缺失行的具体数量和占比,

如结果所示,3000行的数据集中有2024行存在缺失值,缺失行的比例约67.47%。不管是变量角度的缺失值判断,还是数据行角度的缺失值判断,一旦发现缺失值,都需要对其作相应的处理,否则一定程度上都会影响数据分析或挖掘的准确性。
四,探索缺失值的模式
在决定如何处理缺失数据前,了解哪些变量有缺失值、数目有多少、是什么组合等信息,是非常有用的。
1,可视化缺失值的分布
查看缺失值的缺失数量以及比例
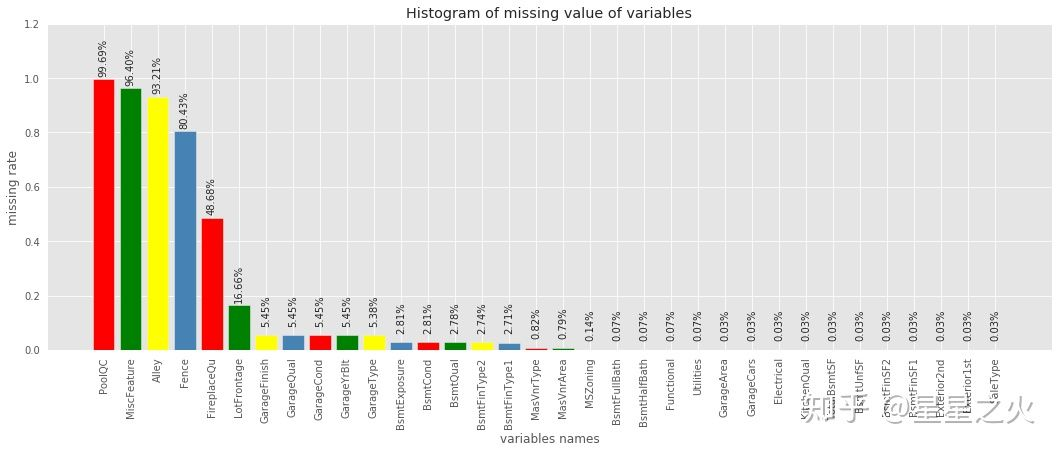
import pandas as pd # 统计缺失值数量 missing=data.isnull().sum().reset_index().rename(columns={0:'missNum'}) # 计算缺失比例 missing['missRate']=missing['missNum']/data.shape[0] # 按照缺失率排序显示 miss_analy=missing[missing.missRate>0].sort_values(by='missRate',ascending=False) # miss_analy 存储的是每个变量缺失情况的数据框 import matplotlib.pyplot as plt import pylab as pl fig = plt.figure(figsize=(18,6)) plt.bar(np.arange(miss_analy.shape[0]), list(miss_analy.missRate.values), align = 'center' ,color=['red','green','yellow','steelblue']) plt.title('Histogram of missing value of variables') plt.xlabel('variables names') plt.ylabel('missing rate') # 添加x轴标签,并旋转90度 plt.xticks(np.arange(miss_analy.shape[0]),list(miss_analy['index'])) pl.xticks(rotation=90) # 添加数值显示 for x,y in enumerate(list(miss_analy.missRate.values)): plt.text(x,y+0.12,'{:.2%}'.format(y),ha='center',rotation=90) plt.ylim([0,1.2]) plt.show()
这样的统计计算以及可视化基本已经看出哪些变量缺失,以及缺失比例情况,对数据即有个缺失概况。
2,用相关性探索缺失数据
变量之间有时存在很强的相关性,有时候,某一个变量缺失会导致其他变量也缺失,这就是缺失数据之间的相关性。
用指示变量代替数据集中的数据(1代表缺失,0代表存在),这样生成的矩阵有时被称作影子矩阵,求这些指示变量之间的相关性,有助于观察哪些变量经常一起缺失。
missing=data.isnull() corr_matrix = missing.corr() corr_matrix["missing_variable"].sort_values(ascending=False)
五,缺失数据的处理
识别缺失数据的数目、分布和模式,有两个目的:分析生成缺失数据的潜在机制,评价缺失数据对回答实质性问题的影响。具体来讲,需要弄清楚以下几个问题:
- 缺失数据的比例有多大?
- 缺失数据是否集中在少数几个变量上,抑或广泛存在?
- 缺失是随机产生的吗?
- 缺失数据间的相关性或与可观测数据之间的相关性,是否可以表明产生缺失值的机制。
回答这些问题将有助于采用合适的方法来处理缺失数据。
- 如果缺失数据集中在几个相对不重要的变量上,那么可以删除这些变量。
- 如果有一小部分数据(如小于10%)随机分布在整个数据集中(MCAR),那么你可以删除存在缺失数据的行,而只分析数据完整的实例,这样扔可以得到可靠且有效的结果。
- 如果可以假定数据是MCAR或MAR,那么可以应用多重插补法来获得有效的结论。
1,推理恢复
根据变量之间的关系来填补或恢复缺失值,通过推理,数据的恢复可能是准确无误的或近似准确的,例如,如果一个数据对象的age是20,那么该人的学历大概率是学士。
2,删除法
删除法是指将缺失值所在的行删除(前提是变量缺失的比例非常低,如5%以内),或者删除缺失值所对应的变量(前提是该变量中包含的缺失值比例非常高,比如80%左右)。把包含一个或多个缺失值的行删除,称作行删除法,或个案删除(case-wise deletion),大部分统计软件包默认采用的是行删除法。
# 删除字段,例如删除缺失率非常高的edu变量 df.drop(labels = 'edu', axis = 1, inplace=True)
如果变量的缺失比例非常大,或者行缺失的比例非常小,那么使用删除法是一个不错的选择,反之,删除发将会使模型丢失大量的数据信息而得不偿失。
删除法的缺点:
- 牺牲了大量的数据,通过减少历史数据换取完整的信息,这样可能丢失了很多隐藏的重要信息;
- 当缺失数据比例较大时,特别是缺失数据非随机分布时,直接删除可能会导致数据发生偏离,比如原本的正态分布变为非正太;
这种方法在样本数据量十分大且缺失值不多的情况下非常有效,但如果样本量本身不大且缺失也不少,那么不建议使用。
3,均值替换法
均值替换法也叫均值插补,是指对存在缺失值的变量,直接利用该变量的均值、中位数或众数替换该变量的缺失值,其好处是缺失值的处理速度快,缺点是容易产生有偏估计,导致缺失值替换的准确性下降。
把数据集的属性分为定性属性和定量属性来分别进行处理:
- 如果变量是数值型的,那么计算该变量在其他所有数据行的取值的平均值或中位数来替换缺失值;
- 如果变量是文本型的,那么根据统计学中的众数原理,计算出该属性在其他所有数据行的取值次数最多的值(即出现频率最高的值)来替换缺失值。
这就意味着,对于定性数据,使用众数(mode)填补,比如一个学校的男生和女生的数量,男生500人,女生50人,那么对于其余的缺失值,我们会用人数较多的男生来填补。对于定量(定比)数据,使用平均数(mean)或中位数(median)填补,比如一个班级学生的身高特征,对于一些同学缺失的身高值就可以使用全班同学身高的平均值或中位数来填补。
一般情况下,如果特征分布为正太分布时,使用平均值效果比较好,而当分布由于异常值存在而不是正太分布的情况下,使用中位数效果比较好。
替换法对于非MCAR的数据会产生有偏向的结果,适用于缺失数据的数量较小的数据集。均值替换是在低缺失率下首选的插补方法,缺点是不能反映缺失值的变异性。
# 替换法处理缺失值 df.fillna(value = {'gender': df['gender'].mode()[0], # 使用性别的众数替换缺失性别 'age':df['age'].mean() # 使用年龄的平均值替换缺失年龄 }, inplace = True )
缺失值的填充使用的是fillna()方法,其中value参数可以通过字典的形式对不同的变量指定不同的值。需要强调的是,如果计算某个变量的众数,一定要使用索引技术,例如代码中的[0],表示取出众数序列中的第一个(我们知道,众数是指出现频次最高的值,假设一个变量中有多个值共享最高频次,那么Python将会把这些值以序列的形式存储起来,故取出指定的众数值,必须使用索引)。
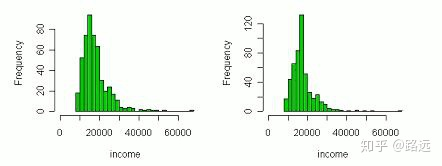
注:此方法虽然简单,但是不够精准,可能会引入噪声,或者会改变特征原有的分布。下图左为填补前的特征分布,图右为填补后的分布,明显发生了畸变。因此,如果缺失值是随机性的,那么用平均值比较适合保证无偏,否则会改变原分布。
4,随机差值
采用某种插入模式进行填充,比如取缺失值前后值的均值进行填充:
# interpolate()插值法,缺失值前后数值的均值,但是若缺失值前后也存在缺失,则不进行计算插补。 df['a'] = df['a'].interpolate() # 用前面的值替换, 当第一行有缺失值时,该行利用向前替换无值可取,仍缺失 df.fillna(method='pad') # 用后面的值替换,当最后一行有缺失值时,该行利用向后替换无值可取,仍缺失 df.fillna(method='backfill')#用后面的值替换
5,插补法
请阅读《机器学习 第3篇:》
参考文档: