突发奇想,可以把每天学的东西搞成个问答形式,就像理想国那种对话形式,有点不好说清楚的东西这样一来就能表达的很生动很清楚了!(还可以看着问题回想答案
内容选材上尽量都是基本、常用且重要的知识点。尽量简洁。
(打字好麻烦,还是在笔记本上写字方便。也不知道做这个能做多久)
问:概率与统计的区别是什么?
答:看笔记本
问:什么是似然函数?
答:似然函数p(x|θ):当x是已知确定的,θ是变量,p(x|θ)这个函数叫做似然函数。
当θ是已知确定的,x是变量,p(x|θ)这个函数叫做概率函数。
问:最大似然估计(MLE)是什么?
答:求参数θ,使似然函数p(x|θ)最大。
问:那怎么理解呢?
答:在事件x发生的前提下,找出使事件x发生概率最大的参数θ。
问:最大后验概率估计(MAP)是什么?
答:求参数θ,使p(x|θ)p(θ)最大。
问:怎么理解呢?
答:就是说,求得的θ不仅仅让似然函数大,θ自己出现的概率(先验概率)也得大。有点像正则化加入惩罚项的感觉。
此外,p(θ|x) = p(x|θ)p(θ) / p(x) , 被称为后验概率。
问:停,后验概率p(θ|x)与似然函数p(x|θ)有什么区别?还有p(x|θ)不是还可以是概率函数嘛?你怎么指定他是似然函数还是概率函数?
答:先回答第二个问题,上面问'什么是似然函数'那里不是说了吗。而且不用指定,就是直接能知道的啊。
后验概率p(θ|x)是在x发生前提下,某个θ的概率,他是一个从逻辑上讲只关于θ的概率;
似然函数p(x|θ)是在x发生前提下,θ取值为θ时(能明白吧?)x发生的概率。他是一个从逻辑上讲关于x的概率。这里举例:x发生了,若θ=0.3,则x发生的概率为0.5;若θ=0.1,则x发生的概率为0.9。很明显,既然x已经发生了,那么θ等于0.1的概率要远远大于0.3。因为x都已经发生了啊。
问:马尔可夫毯(markov blanket)是什么?
答:马尔可夫毯是贝叶斯网络中的概念。给定一个节点T,他的MB是唯一的,包括T的所有父、子和配偶(和T有共同孩子的)节点,如下图:
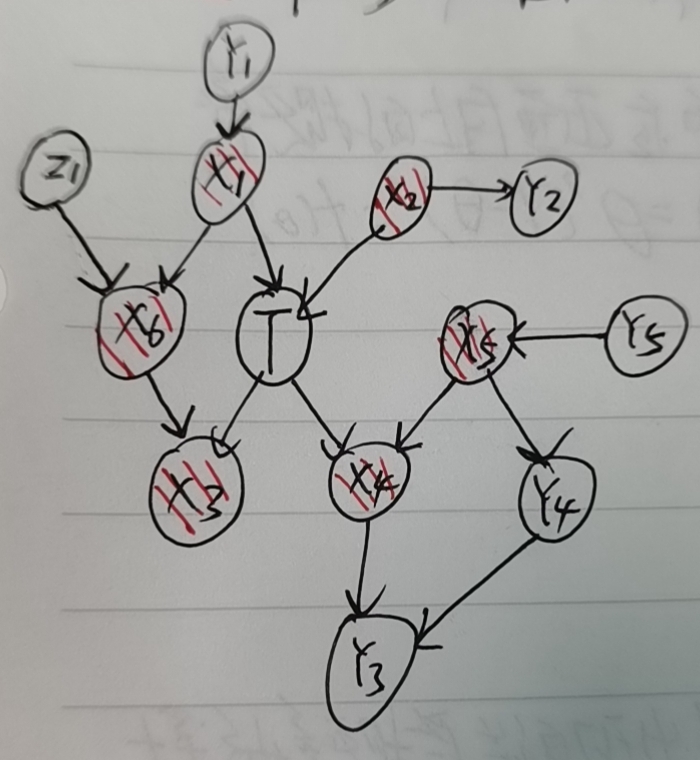
问:那什么是马尔可夫边界(markov boundary)呢?
答:变量T的MB是U(变量的完整集合)的任何最小子集,它使得U的其余部分与T无关。