
sol
输入n和H表示n个人,选H个人gcd最大
抓住排列,是x[1,n]的正整数,是连续的整数,
假设现在最大的公因数是k其中k一定是在[1,n]那么在排列中最多出现的个数为w
那么kw是最大的含有因数k的数字满足kw<=n所以k<=n/w
显然w越小答案k越大而w取值范围是[H,n]所以w=H时答案最大
所以 k(max)=n/H
由于选的序号最小那么for一遍按顺序输出即可
复杂度O(n)
# include <bits/stdc++.h> using namespace std; const int MAXN=500005; int a[MAXN]; int main() { freopen("dst.in","r",stdin); freopen("dst.out","w",stdout); int n,k; scanf("%d%d",&n,&k); for (int i=1;i<=n;i++) scanf("%d",&a[i]); int temp=n/k; printf("%d ",temp); int cnt=0; for (int i=1;i<=n;i++) if (!(a[i]%temp)) { printf("%d ",i),cnt++; if (cnt==k) break; } return 0; }

sol
设F[i]为斐波那契数列的第i项,显然f[i]=f[i-2]+f[i-1]
一个有趣的结论 gcd(f[a],f[b])=f[gcd([a],[b])]
证明:
设n<m,设第f(n)与f(n+1)为a,b,则有:
首先 证明:gcd(F[n+1],F[n])=1;
辗转相减法:
gcd(F[n+1],F[n])
=gcd(F[n+1]-F[n],F[n])
=gcd(F[n],F[n-1])
=gcd(F[2],F[1])
=1
x f(x) 1 1 2 1 3 2 4 3 5 5 ... n a n+1 b n+2 a+b n+3 a+2b n+4 2a+3b n+5 3a+5b ...
m f[m-n-1]a+f[m-n]b
因为gcd(m,n)=gcd(n,m%n)
所以 gcd(f(m),f(n))=gcd(f(n),f(m)%f(n))=gcd(a,f(m-n)b)
a,b相邻 gcd(a,b)=1;
f(n)=a【逃这应该看得出来吧】
gcd(f(m),f(n))=gcd(f(n),f(m-n))
辗转相减法 就是gcd(f(n),f(m%n))
辗转相除法 就是f(gcd(n,m))
对于20%的数据,0<n,m<100000 随便线性推一推就行
对于60%的随机数据 ,找到规律线性递推求斐波那契数列即可
对于100%的数据 n,m<=10^14,找到规律,用矩阵快速幂优化递推就行
单位矩阵这样的:
f[i-1] f[i-2] 1 1 f[i] f[i-1] 0 0 1 0 0 0
复杂度O(log n)
# include <bits/stdc++.h> using namespace std; typedef long long ll; const int mo=233333333,MAXN=100005; struct Node{ ll m[2][2]; }; Node tt; ll gcd(ll a,ll b) { return b==0?a:gcd(b,a%b); } Node mul(Node a,Node b) { Node t; for (int i=0;i<=1;i++) for (int j=0;j<=1;j++) { ll sum=0; for (int k=0;k<=1;k++) sum=(sum+a.m[i][k]*b.m[k][j]%mo)%mo; t.m[i][j]=sum%mo; } return t; } Node pow(Node x,ll n) { if (n==1) return tt; Node t=pow(x,n/2); t=mul(t,t); if (n%2==1) t=mul(t,x); return t; } int main() { freopen("st.in","r",stdin); freopen("st.out","w",stdout); /* f[] a,b g=gcd(a,b); f[g]=gcd[f[a],f[b]]; */ ll n,m; scanf("%lld%lld",&n,&m); if (n>m) swap(n,m); ll g=gcd(n,m); if (g==1ll||g==2ll) { printf("1 "); return 0; } Node k; k.m[0][0]=1,k.m[0][1]=1; k.m[1][0]=1;k.m[1][1]=0; tt=k; Node w=pow(k,n-1); printf("%lld ",w.m[0][0]%mo); return 0; }

sol
错排问题的模板问题
假设A...为信封,a...为信件
我假设把a放B里,显然是一个错放,在这里我们可以看到这个错误出现的类型有两大类:(
就是导致这个错放的原因)
- b错放到A里,此时,b错放到A;a错放到B;后面的C..和A,B没有关系了,后面n-2个信封全错排 就是f(n-2)
- b错放到除了A、B之外的一个信封,剩下的n-1个信封全错排就能符合条件放法总数为f(n-1)
总而言之,在a错放到B里,共有错放法:f(n-2)+f(n-1)这么多种,
在a错放到C,错放到D……(n-1)种可能的情况下,同样有f(n-2)+f(n-1)种错放法,因此得出错放总数为
f(n)=(n-1){f(n-2)+f(n-1)}
复杂度O(n)
# include <bits/stdc++.h> using namespace std; typedef long long ll; const int mo=1e9+7,MAXN=100005; ll f[MAXN]; int main() { freopen("jdt.in","r",stdin); freopen("jdt.out","w",stdout); int n; while(~scanf("%d",&n)) { f[1]=0;f[2]=1; for (int i=3;i<=n;i++) f[i]=(i-1)*((f[i-2]+f[i-1])%mo)%mo; printf("%lld ",f[n]); } return 0; }
二项式反演
上个公式:
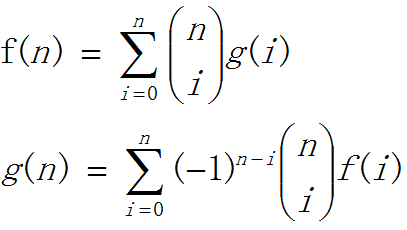
f(n)表示n个数的全排列,即 f(n)=n!
g(i)有n个信封中有i个信封错排,g(n)就是我们要求的结果。
f(n)= C(n,0)g(0) + C(n,1) g(1) ….+C(n,n) * g(n)
从n里面选0,1,2...n错排总数和就是全排列
因为对于全排列有2种可能:
1.正确摆放 (1)
2.有i个错误摆放 (0<i<=n)
归纳一下就是有i个错误摆放 (0=<i<=n)
反演一下就ok
g(n)=∑(-1)^(n-i) * C(n,i) * i! (从0到n)
C(n,i)的时候暴力搞一下逆元。
复杂度O(n)
std是这种方法:
#include <cstdio> #include <algorithm> #include <iostream> #define LL long long using namespace std; int n; const LL MOD=1e9+7; const int MAXN=100010; LL f[MAXN],t[MAXN]; void fff(){ freopen("jdt.in","r",stdin); freopen("jdt.out","w",stdout); } void fction(){ f[0]=1; for (int i=1;i<=100010;i++)f[i]=(f[i-1]*i)%MOD; t[0]=t[1]=1; for (int i=2;i<=100010;i++)t[i]=((MOD-MOD/i)%MOD)*(t[MOD%i]%MOD)%MOD; for (int i=2;i<=100010;i++) t[i]=(t[i]*t[i-1])%MOD; } int main(){ fff(); fction(); while (scanf("%d",&n)!=EOF){ LL ans=0; LL flag=n&1?-1:1; for (int i=0;i<=n;i++){ ans=(ans+(flag*1ll*((f[n]%MOD)*t[n-i])%MOD))%MOD; flag=-flag; } ans=(ans+MOD)%MOD; printf("%lld ",ans); } }