地址:http://acm.hdu.edu.cn/showproblem.php?pid=6898

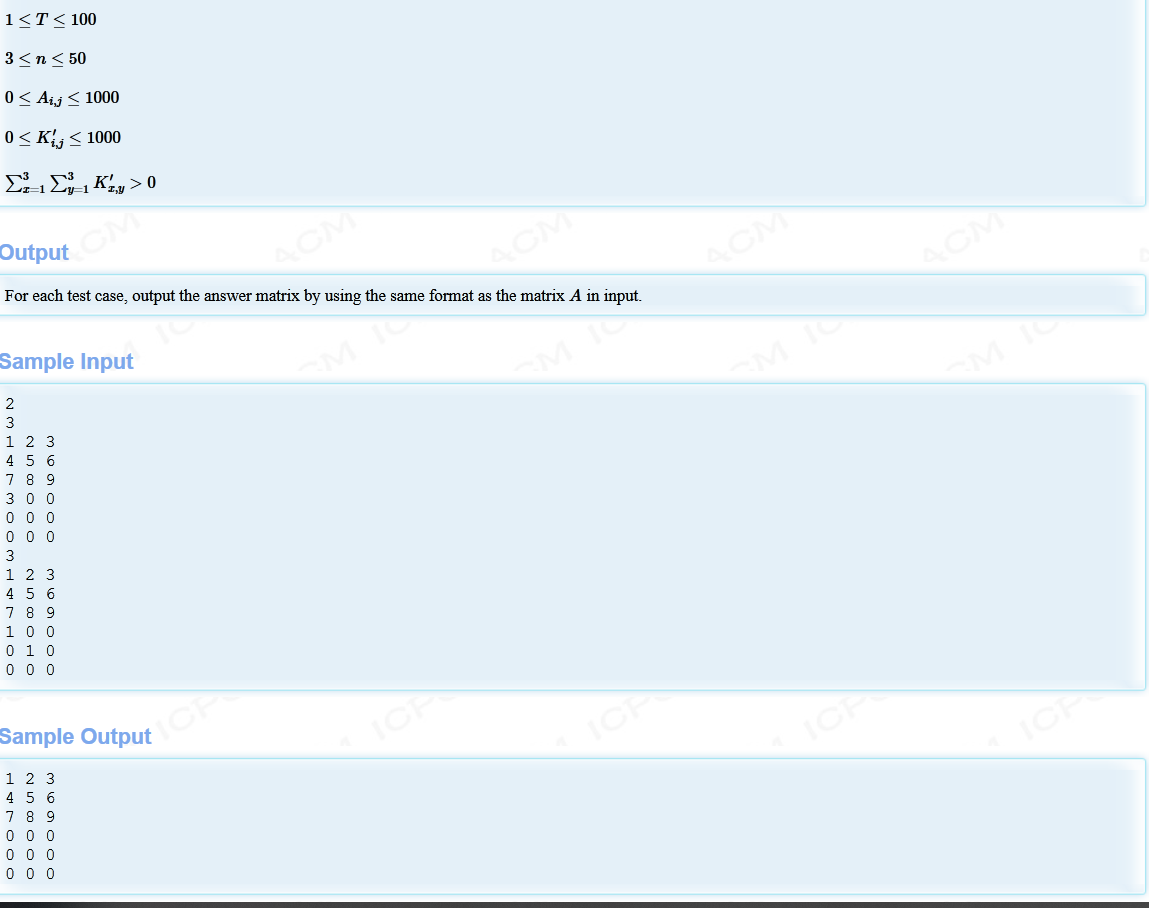
队友A掉的题。赛后看了下,觉得有必要好好写一个题解。
题意:
给出A,K',求C
而C需要K,所以需要通过K'求K
解析:
1:暴力做法
由题中公式,先求K,然后直接四层for求出C来,打印即可。
#include <bits/stdc++.h> #include<vector> using namespace std; typedef long long ll; const int maxn = 1e3+10; vector<int>g[maxn]; int main(){ int t; cin>>t; while(t--) { int mp[55][55],k[4][4]; int c[55][55]; memset(c,0,sizeof(c)); int n; cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>mp[i][j]; int sum=0; for(int i=1;i<=3;i++) for(int j=1;j<=3;j++) { cin>>k[i][j]; sum+=k[i][j]; } for(int i=1;i<=3;i++) { for(int j=1;j<=3;j++) { k[i][j]=k[i][j]/(sum*1.0); } } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { for(int o=1;o<=min(n-i+1,3);o++) { for(int p=1;p<=min(n-j+1,3);p++) { c[i][j]+=mp[i+o-1][j+p-1]*k[o][p]; } } } } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(j<n) cout<<(int)c[i][j]<<" "; else cout<<(int)c[i][j]<<endl; } // cout<<endl; } } }
2:思维做法
这里就得详细得写一下了。
首先对于C的公式:
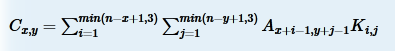
画一下,就可以发现,对于Ci,j,在A中就是以Ai,j为左上角到右下角的范围,其同样大小的范围放在K中,K中一定是以K1,1做为左上角。对应位置两两相乘,再相加即可。
举个对应关系:
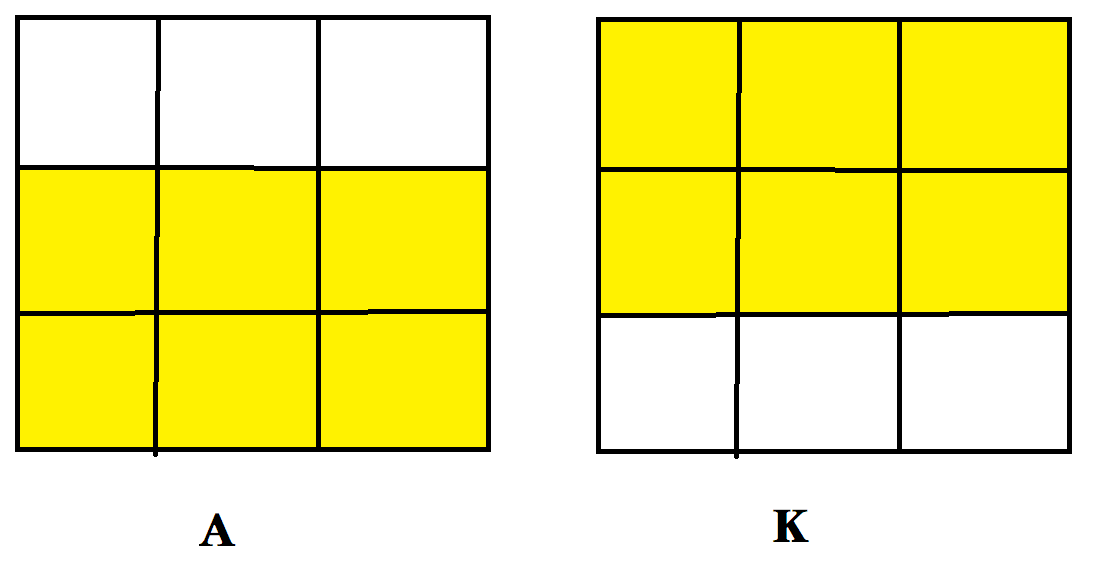
然后再看这个无穷:
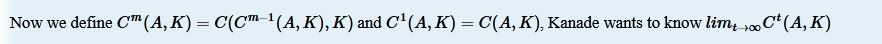
首先求C^1,然后C^1变成了新的A,也就是每次算出的矩阵C,都要在下一步做为A与K进行运算。
拿样例2举例:

(1)发现,无穷次乘,C1,1就要无限乘1/2,它只会越乘越小,最后趋于0,其他元素也是如此。
所以对于K'中如果出现多个数字,那么K中一定会出现小数(sum==1,其一定小于1),一个数无限乘一个小于1的小数,最后一定趋向于0。
所以如果K'出现了多个数,结果一定全0.
(2)如果K'只出现了一个数,那么这个数一定为1。重要的是它的位置。
观察C的计算公式,发现K1,1是必然要算的,所以如果1在K1,1位置,那么无穷次,C必然不变。
如果1在其他位置,最后一定会趋向于0的,这个随便举个例子就可以说明的。
所以总的结论就是:
i=1,j=1之外出现了非0数,输出全0,否则输出原C。
#include <bits/stdc++.h> #include<vector> using namespace std; typedef long long ll; const int maxn = 1e3+10; vector<int>g[maxn]; int a[maxn]; int b[maxn]; int vis[maxn]; int ok = 0 ; int x,y; int mp[maxn][maxn],k[4][4]; int main(){ int t; cin>>t; while(t--) { int n; cin>>n; int ok=0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>mp[i][j]; for(int i=1;i<=3;i++) for(int j=1;j<=3;j++) { cin>>k[i][j]; if(i!=1&&j!=1&&k[i][j]!=0) { ok=1; } } if(ok) { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(j<n) cout<<"0"<<" "; else cout<<"0"<<endl; } // cout<<endl; } }else { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(j<n) cout<<mp[i][j]<<" "; else cout<<mp[i][j]<<endl; } } } } }