地址:http://codeforces.com/contest/1337
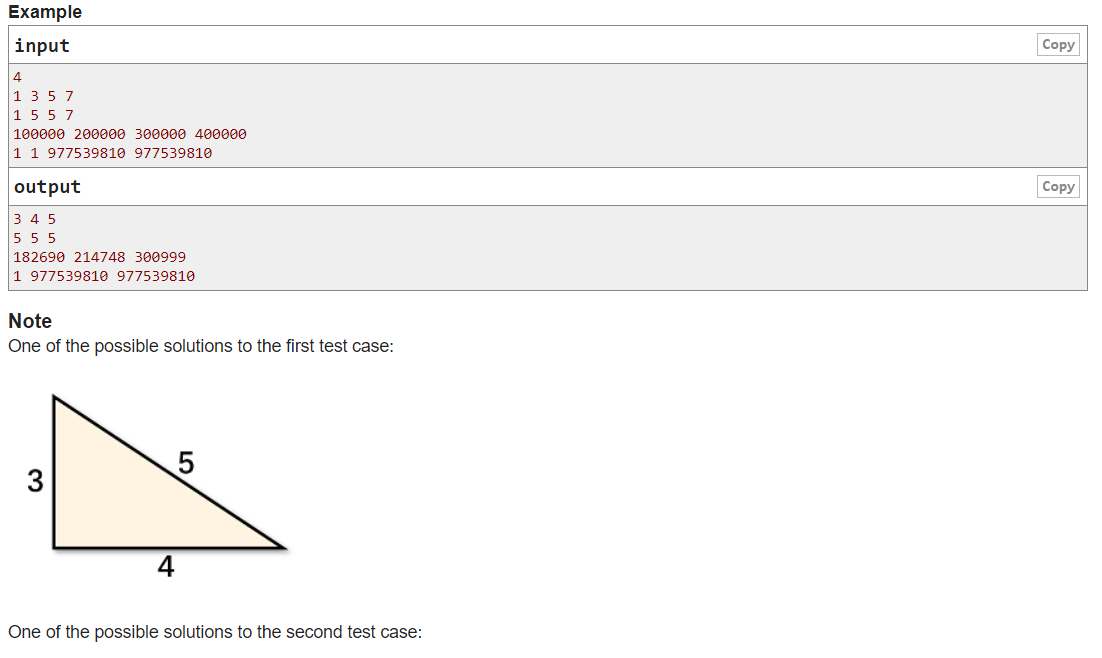

题意:给出a,b,c,d。从a~b~c~d三个区间内各找一个数,构成三角形。
解析:根据三角形的性质,输出a,c,c是一个可行解。记得从小到大输出,wa了1次。
#include<iostream> #include<vector> #include<cstring> using namespace std; typedef long long ll; const int maxn=1e5+10; const int inf = 0x3f3f3f3f; int main() { int t; cin>>t; while(t--) { ll a,b,c,d; cin>>a>>b>>c>>d; cout<<a<<" "<<c<<" "<<c<<endl; } }

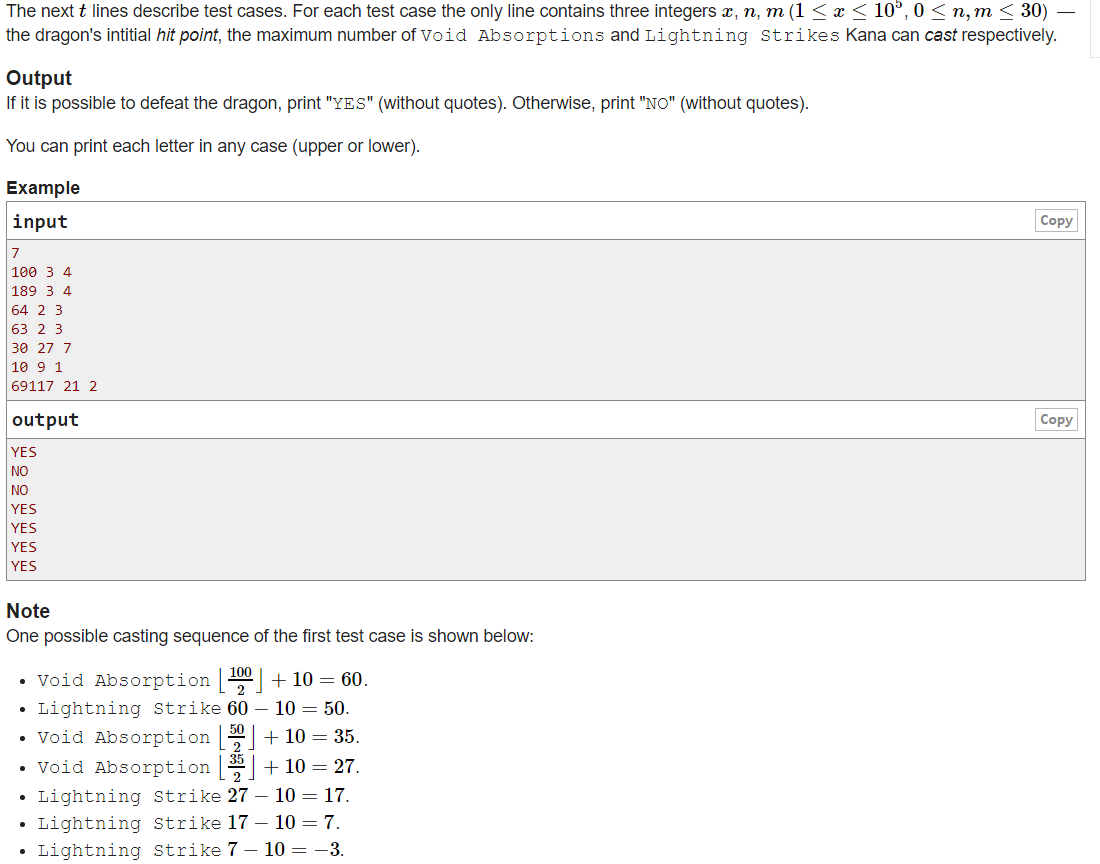
题意:x,n,m。龙有x滴血,有操作:血量/2+10 -> 最多n次。血量-10->最多m次。问是否能把龙杀掉
解析:对于操作一,可以看出,当血量<20,/2+10这个值是要增大的。所以我们先进行操作一,当<20时break掉。然后把这个剩余血量-10*m,看是否小于0。
#include<iostream> #include<vector> #include<cstring> using namespace std; typedef long long ll; const int maxn=1e5+10; const int inf = 0x3f3f3f3f; int main() { int t; cin>>t; while(t--) { int x,n,m; cin>>x>>n>>m; int cnt=0; int k=x; for(int i=1;i<=n;i++) { x=x/2+10; if(x<20) break; k=x; } // cout<<k<<endl; k=k-m*10; if(k>0) cout<<"NO"<<endl; else cout<<"YES"<<endl; } }
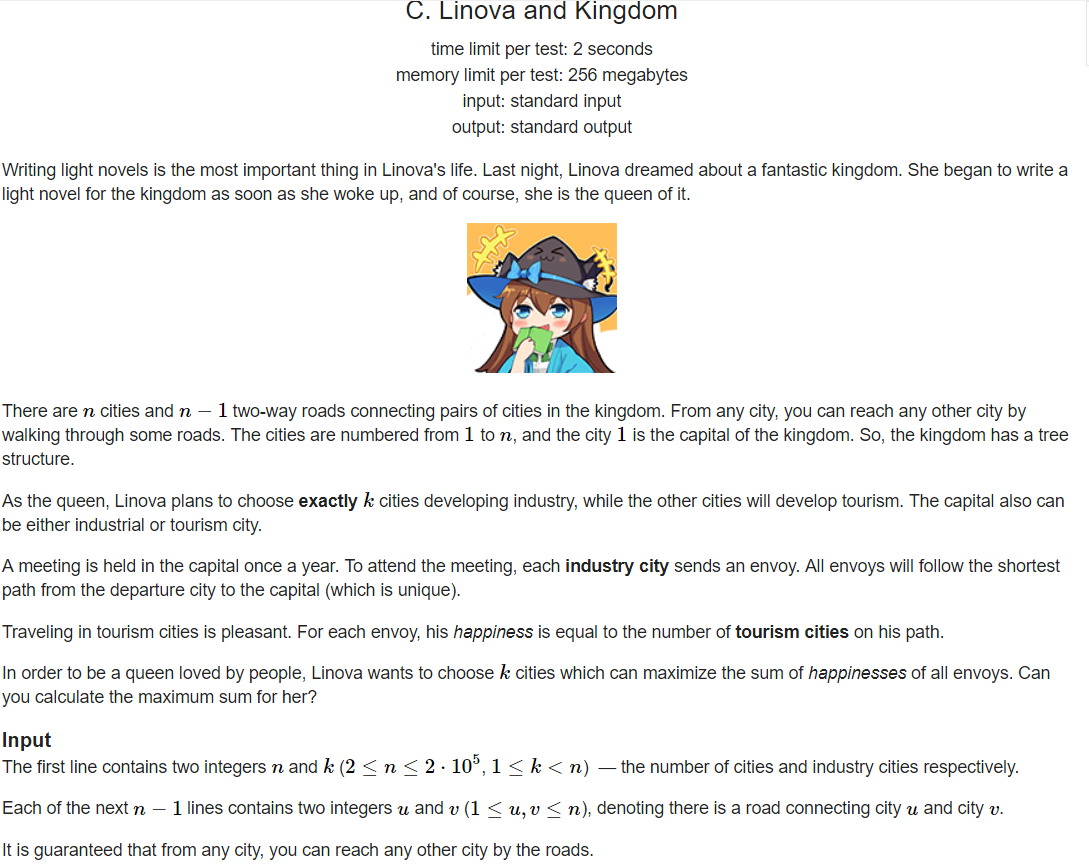

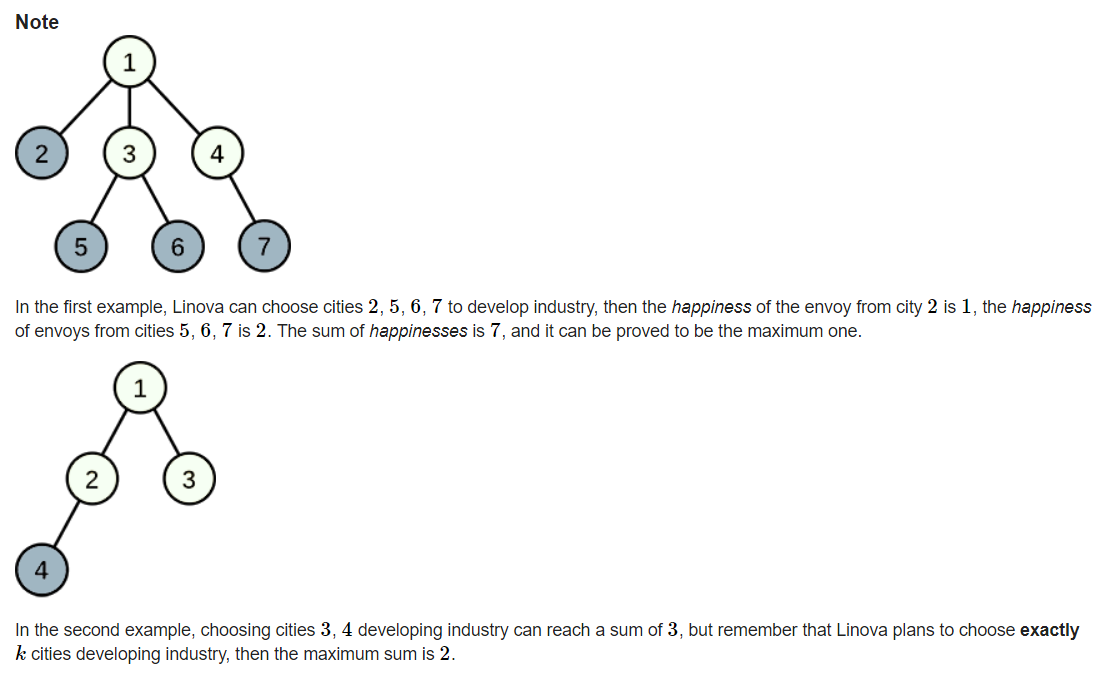
题意:给出一个1~n点都含有的完整的树,只有一个根。每个点都是一个城市。现在要把k个城市变成工业城市,其他变成旅游城市。这些工业城市各出一个人去1号点,让他们沿途经过的旅游城市最大,输出这个值。
解析:比赛时只纠结这个入度问题了,思维没有往外扩。这里不用考虑最短路的问题,因为这个树是没有环的。取k个点,第一个想到的,就是从深度最深的点开始取。深度是当前这个点到达1号点经过的点数,比如样例1,deep[5]=2。将深度从大到小排个序,在取的过程中,会出现一个问题,假设我取到了F点,那么它的子节点也一定被取了,那么子节点到1号点所经过的旅游城市数就变了。也就是说,取一个点,那么它的子节点到达1号点所经过的旅游城市数都要-1。所以需要记录点的子节点数size。那么每个点的贡献就是:deep[i]-(size[i]-1)。为什么-1呢,因为size[i]包含了i本身,算的时候要去掉。
采用了链式前向星来存图,关于它,我推荐这位大佬的讲解:https://blog.csdn.net/sugarbliss/article/details/86495945
关于求deep[]和size[]的过程,采用了dfs的回溯,即对一个点,找出它的所有子节点,然后再从子节点回到1号点,这中间把deep[]和size[]累加出来。这个过程需要自己好好体会的,这里为方便小白我给出样例1 的dfs过程:
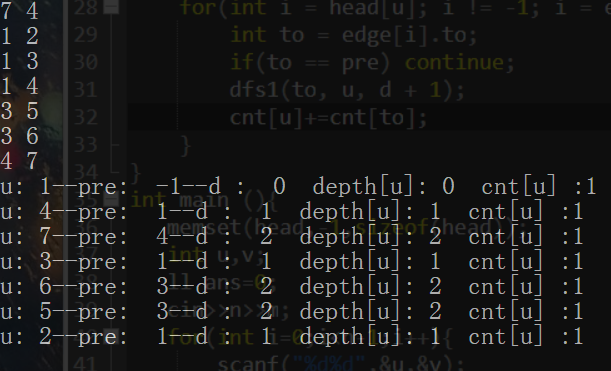
#include<stdio.h> #include<iostream> #include<algorithm> #include<string.h> #include<vector> #include<cmath> #include<string> #include<map> #include<queue> using namespace std; typedef long long ll; const int maxn=2e5+10; int head[maxn],deep[maxn],siz[maxn]; int cnt=0; struct node { int to,nxt; }edge[4*maxn]; void add(int u,int v) { edge[cnt].to=v; edge[cnt].nxt=head[u]; head[u]=cnt++; } void dfs(int u,int v,int d) { deep[u]=d; siz[u]=1; for(int i=head[u];i!=-1;i=edge[i].nxt) { int to=edge[i].to; if(to==v) continue; dfs(to,u,d+1); siz[u]+=siz[to]; } } int main() { int n,k; memset(head,-1,sizeof(head)); cin>>n>>k; int a,b; for(int i=1;i<n;i++) { cin>>a>>b; add(a,b); add(b,a); } dfs(1,-1,0); for(int i=1;i<=n;i++) { deep[i]-=(siz[i]-1); } sort(deep+1,deep+1+n); ll sum=0; int j=n; for(int i=1;i<=k;i++) { sum+=deep[j]; j--; } cout<<sum<<endl; }
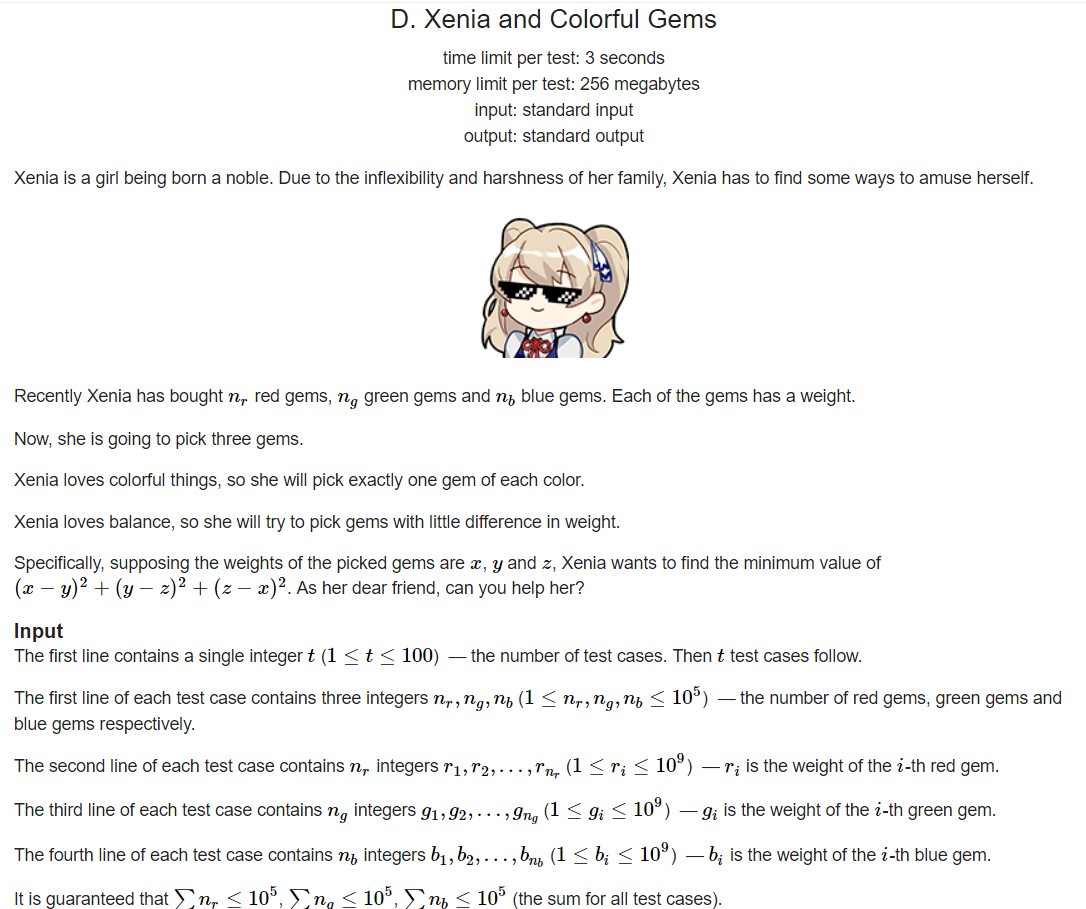

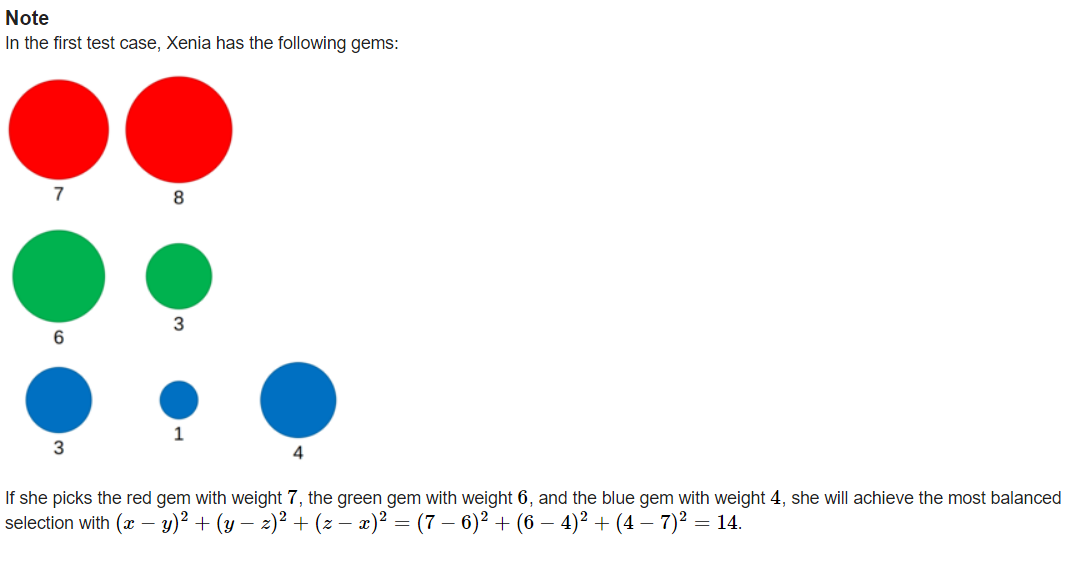
题意:题意很简单,给出三组数,每组选一个,使(a-b)*(a-b)+(a-c)*(a-c)+(b-c)*(b-c)最小。
解析:先想到的是暴力,但是复杂度太高O(n3)。所以可以考虑通过枚举其中一个数组,从另外两个数组中拿数来算最小值。观察一下这个式子,要想最小化,x,y,z三者的两两距离一定要最小。而且对于三者关系,无外乎就这六种关系:b>=a>=c b>=c>=a a>=b>=c a>=c>=b c>=a>=b c>=b>=a。 举个例子,固定a数组的x,找出离它最近的y,z。可以通过二分查找,这里直接用了lower_bound()来找。找到y,z还不算完,因为我们要把上面那六种关系全弄一遍,固定一个数组,我们可以找到三种关系,当前例子即为:x>=y>=z y>=x>=z z>=x>=y 。把找x的这个数组换掉,固定另外俩数组,就可以把6种关系找全了!
建议全开long long,避免不必要的错误。
#include<iostream> #include<cmath> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; typedef long long ll; const ll maxn=1e5+10; ll a[maxn],b[maxn],c[maxn]; const ll inf=2e18+10; ll minn=inf; ll gett(ll a,ll b,ll c) { return (a-b)*(a-b)+(a-c)*(a-c)+(b-c)*(b-c); } void ac(ll a[],ll b[],ll c[],ll n1,ll n2,ll n3) //固定a[],查找b[],c[] { for(int i=0;i<n1;i++) { ll p1,p2; p1=lower_bound(b,b+n2,a[i])-b; p2=lower_bound(c,c+n3,a[i])-c; if(p1==n2) //如果没找到,就退到离a[i]最近的(b[i]<=a[i]) p1--; if(p2==n3) p2--; if(p1>0) minn=min(minn,gett(a[i],b[p1-1],c[p2])); //p1>0,防止-1越界。 if(p2>0) minn=min(minn,gett(a[i],b[p1],c[p2-1])); //同上 minn=min(minn,gett(a[i],b[p1],c[p2])); } } int main() { int t; scanf("%d",&t); while(t--) { ll n1,n2,n3; minn=inf; scanf("%lld%lld%lld",&n1,&n2,&n3); for(int i=0;i<n1;i++) scanf("%lld",&a[i]); for(int i=0;i<n2;i++) scanf("%lld",&b[i]); for(int i=0;i<n3;i++) scanf("%lld",&c[i]); sort(a,a+n1); sort(b,b+n2); sort(c,c+n3); ac(a,b,c,n1,n2,n3); ac(b,a,c,n2,n1,n3); ac(c,b,a,n3,n2,n1); cout<<minn<<endl; } }
