因为最近的生活太颓废总是不做题而被老师D了一番, 所以今天晚上到bzoj上去刷了几道水题。。。。。
bzoj 4320: ShangHai2006 Homework
题目大意
维护一个支持两个操作的集合:
1) 插入一个数x
2) 询问集合中所有数中 mod x 最小是多少
解题思路
似乎log家族没有什么好的办法解决这道题?
考虑 sqrt() 的方法。
当询问 x <= sqrt(m) 的时候, 直接存一下就可以了。
当询问 x > sqrt(m) 的时候,把n分成 n / x 块, 每一块单独考虑。
这时对于每一块, 我们需要求出的就是 >= (i * x) 的所有数中最小的那个。
填一个log会爆掉的。但是如果倒着处理, 每一次询问的就是 x 右面第一个没有被染色的点, 其实就是 疯狂的馒头 这道题, 用并查集搞一搞就可以了。

2 #include<cstdio>
3 #include<cstring>
4 #define MAXN 300003
5 using namespace std;
6 int n,la[MAXN],xx[MAXN],bin[MAXN],ans[MAXN],tmp[MAXN],fat[MAXN],N=300000,sq=570;
7 int find(int x){return x==fat[x]?x:fat[x]=find(fat[x]);}
8 int main(){
9 scanf("%d",&n);
10 memset(tmp,0x7f,sizeof(tmp));
11 memset(ans,0x7f,sizeof(ans));
12 for(int i=1;i<=n;i++){
13 char s[5]; scanf("%s%d",s+1,&xx[i]);
14 la[i]=s[1]-'A';
15 if(!la[i]){
16 bin[xx[i]]++;
17 for(int j=1;j<=sq;j++)tmp[j]=min(tmp[j],xx[i]%j);
18 }else if(xx[i]<=sq)ans[i]=tmp[xx[i]];
19 }
20 for(int i=0;i<=N;i++)if(bin[i])fat[i]=i;else fat[i]=i+1;
21 fat[N+1]=N+1;
22 for(int i=n;i>=1;i--){
23 if(!la[i]){
24 if(!(--bin[xx[i]]))fat[xx[i]]=xx[i]+1;
25 }else if(xx[i]>sq){
26 for(int j=0;j<=N;j+=xx[i])
27 if(find(j)<=N)ans[i]=min(ans[i],find(j)-j);
28 }
29 }
30 for(int i=1;i<=n;i++)if(la[i])printf("%d\n",ans[i]);
31 return 0;
32 }
bzoj 4318: OSU!
题目大意
问一个长度为n, 第i为有pi的概率为1的01串期望的价值是多少。一个01串的价值定义为它的所有极长子只含1串的长度的立方的和。
解题思路
尝试计算每一位对答案的贡献f(i)。 设li 为 i 前面的极长"1"串的长度
显然 f(i) = p[i] * (3 * li2 + 3 * li + 1)。
只要算出 li2 和 li 的期望, 就可以算出 f(i) 的期望了。
注意 li2 的期望并不等于 (li的期望)2 , 要单独存一个数来转移。
虽然恶意缩了缩空格,,但代码真的本来就很短很漂亮。。

using namespace std;
int n;
double ans,x,xx,x2;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lf",&x);
ans+=x*(3*x2+3*xx+1);
x2=x*(x2+2*xx+1);
xx=x*(xx+1);
}
printf("%.1lf\n",ans);
return 0;
}
bzoj 4302: Hdu 5301 Buildings
题目大意
解题思路
构造题。首先旋转一下令 n <= m,显然, 最后答案中覆盖的块一定都是 1 * x 的
其实整个问题的答案就是覆盖了障碍点的 上, 下, 左, 右 四个点的四个块的长度。
这时候情况数就很少了, 分类讨论一下就好了。
1)(障碍物)上面的点向上, 下面的点向下, 这时候剩下的点分两种情况: 1, 全部按照 (n + 1) / 2的方式竖着排列 2, 所有左边的点向左连, 右边的点向右连(其实第2种情况更优当且仅当是一个边长为奇数的正方形且障碍点在中间)
2)(障碍物)上面的点和下面的点都向 左边和右边中更近的那一边连 , 这时候剩下的点(就是障碍物左边的所有点或者是右边的所有点)分两种情况: 1, 全部按照 (n + 1) / 2的方式竖着排列 2, 所有点都向左边/ 右边连。
好了, 其实一共只有四小类。
代码还是炒鸡短。。。

#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdio>
using namespace std;
int n, m, x, y;
int main(){
while(scanf("%d%d%d%d", &n, &m, &x, &y) != EOF){
if(n > m) swap(n, m), swap(x, y);
int ans = max(min((n + 1) / 2, max(y - 1, m - y - 1)), max(x - 1, n - x));
ans = min(ans, max(min(y, m - y + 1), min((n + 1) / 2, max(y - 1, m - y))));
printf("%d\n", ans);
}
return 0;
}
bzoj 4305: 数列的GCD
题目大意
解题思路
因为 300000 以内的数的因子个数最多也就140个, 所以这道题怎么搞一搞都可以。
然后就是一些基本数论知识也没什么好说的。对于每一个i ,只要求出a[]中有多少个数是i的倍数。对于不是i的倍数的那些数, 贡献的方案数是 数量(n/i) , 对于是i的倍数的那些数, 贡献的是 从那么多数中选取(n-k)个数, 选出来的数每个有1种取法,其它的每个有(n/i)-1种取法。
代码有点丑就不贴了(竟然比绝大多数代码都长简直不能忍!!!一定是我的算法太丑了QAQ)
bzoj 3884: 上帝与集合的正确用法
题目大意
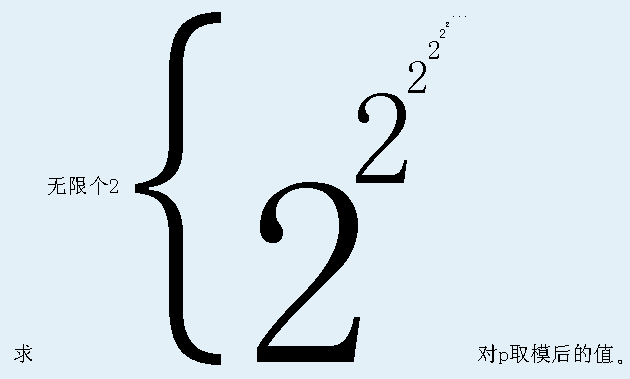
解题思路
我们都知道欧拉定理: an ≡ an mod φ(p) mod p (gcd(a, p) = 1)
然而它竟然还有一个拓展:
然后这道题就可以随便做了。设答案为 f(x)
于是就可以递归地解决啦

2 #include <cstdio>
3 #include <cstring>
4 #include <cmath>
5 #include <algorithm>
6 #define N 10000000
7 #define ll long long
8 using namespace std;
9 int t, phi[N + 5], prim[N], pp, f[N+5], X[1005], mx;
10 bool isp[N+5];
11 int mypow(int x, int k, int mod){
12 int ret = 1;
13 while(k){
14 if(k & 1) ret = (ll)ret * x % mod;
15 x = (ll)x * x % mod; k >>= 1;
16 }return ret;
17 }
18 int calc(int x){
19 if(f[x] == -1) f[x] = mypow(2, calc(phi[x]) + phi[x], x);
20 return f[x];
21 }
22 int main(){
23 scanf("%d", &t);
24 for(int i = 1; i <= t; i ++) scanf("%d", &X[i]), mx = max(mx, X[i]);
25 for(int i = 2; i <= mx; i ++){
26 if(!isp[i]) prim[++ pp] = i, phi[i] = i - 1;
27 for(int j = 1; j <= pp && (ll)i * prim[j] <= mx; j ++){
28 isp[i * prim[j]] = 1; phi[i * prim[j]] = phi[i] * (prim[j] - 1);
29 if(i % prim[j] == 0) {phi[i * prim[j]] = phi[i] * prim[j]; break;}
30 }
31 }
32 memset(f, -1, (mx + 2) * 4);
33 f[1] = 0;
34 for(int i = 1; i <= t; i ++) printf("%d\n", calc(X[i]));
35 // system("pause");
36 return 0;
37 }
