转载:https://www.cnblogs.com/bigmonkey/p/11929491.html
作者: 我是8位的
欧拉公式被誉为“宇宙第一公式”,是大名鼎鼎的莱昂哈德·欧拉提出的。这位老大哥提出了很多著名的公式和定理,我们在RSA原理中遇到的欧拉函数就是他提出来的,还有图论中那个著名的七桥问题,也是欧拉提出的。

1748年,欧拉在洛桑出版的《Introduction》中第一次出现了一个等式:

这就欧拉恒等式。等式的奇妙之处在于,它将数学中最重要的几个常数联系在一起:两个无理数,自然对数e和圆周率π;两个最简单的常数,1和0;还有单位虚数 i。 欧拉到底是基于什么样的脑回路写下了这个等式?
欧拉公式
预理解欧拉恒等式,必先理解欧拉公式。欧拉公式的形式很简单:

欧拉公式的由来
我们总说站在巨人的肩膀上,其实巨人也是站在另一个巨人的肩膀上,欧拉最早是通过泰勒公式观察出欧拉公式的,把ex在x0=0点展开:
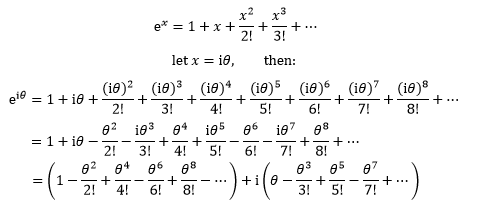
貌似得到了两个更复杂的无穷级数,其实这两个大家伙正是余弦和正弦的泰勒展开式。根据泰勒公式:
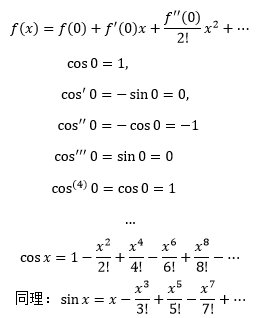
现在eiθ可以变得简单了:
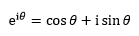
当θ=π时得到欧拉恒等式:

欧拉公式的几何意义
相关阅读:复数和复平面
上一章介绍了极坐标下的复平面,把eiθ映射到极坐标,正好是模长r=1的向量:
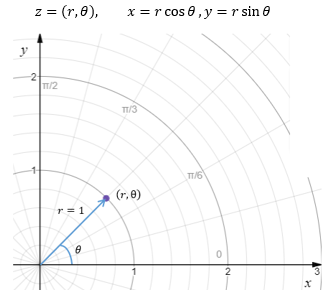
这相当于把(1, 0)沿着原点逆时针旋转了θ,因此eiθ在极坐标下可以看作点绕着圆心在原点,半径是1的圆做圆周运动。
欧拉公式描述的是点在复平面上的圆周运动,把 θ 看作时间,并用 t 代替 θ ,随着时间的改变,这个点在时间轴上变成了一条螺旋线:
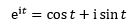
我们用Octave画出这个螺旋线:
t = 0 : 0.02 : 10 * pi; % 在0到10π之间取10π/0.02个时间变量
r = 1; % 半径
x = r * cos(t);
y = r * sin(t);
plot3(x, y, t);
xlabel('x');
ylabel('y');
zlabel('t');
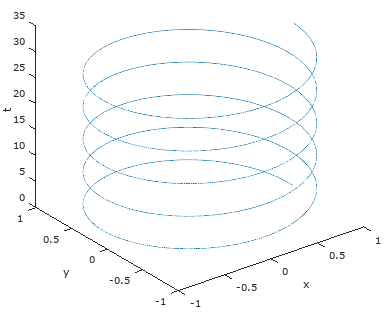
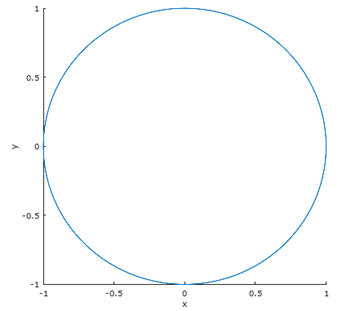
转动这个图形,可以看到欧拉函数在不同坐标系下的曲线。在复平面x-y上,欧拉公式形成了半径为1的单位圆:
在x-t平面上,欧拉公式形成了余弦曲线,是eit=cost + isint的实数部分:
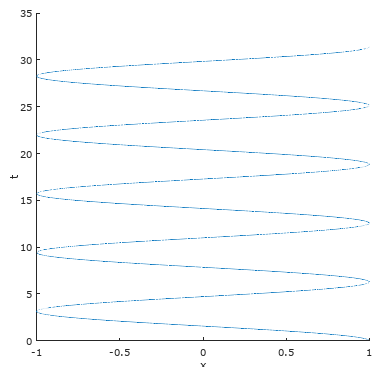
在y-t平面上,欧拉公式形成了正弦曲线,是eit=cost + isint的虚数部分:
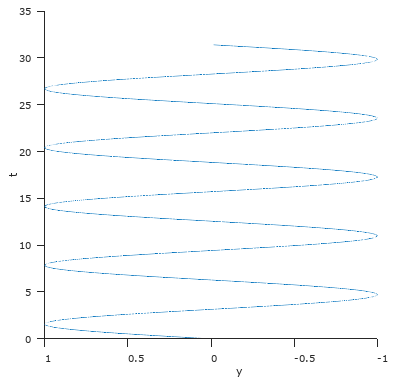
可以看到,欧拉公式把正弦波和余弦波用指数形式统一起来。随着时间的推移,点在时间轴上形成了螺旋线,在实轴和虚轴上形成了余弦和正弦曲线。

欧拉函数的核心是旋转和频率,现代物理学又告诉我们,世界和微观世界都是旋转的,从这个意义上来说,欧拉函数还真是宇宙第一公式。
