本文是对网络上几篇文章的总结,主要是方便自己后期翻看不至于太过混乱,如有侵权,请留言~
参考文章为:
1) https://zhuanlan.zhihu.com/c_141391545
2) https://zhuanlan.zhihu.com/p/34355703
3) https://zhuanlan.zhihu.com/p/34222451
4) https://www.cnblogs.com/skyfsm/p/6790245.html
5) http://ctolib.com/docs-Tensorflow-c-Tensorflow4.html
6) https://zhuanlan.zhihu.com/p/33841176
1、卷积神经网络简介:
1.1、卷积神经网络共分为几个层次,基本的卷积神经网络是由以下部分组成的,更为复杂的卷积神经网络是这些层次的组合:
1) 数据输入层(Input layer)
2) 卷积计算层(CONV layer)
3) ReLU激励层(ReLU layer)
4) 池化层(Pooling layer)
5) 全连接层(FC layer)
1.2、整体流程为:
1)可视图:
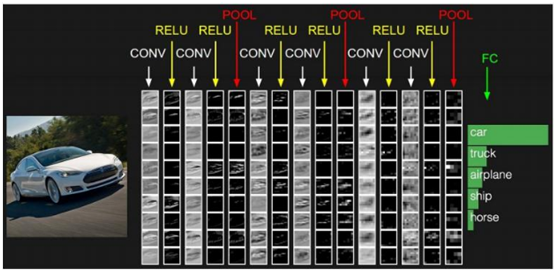
2)数据流:
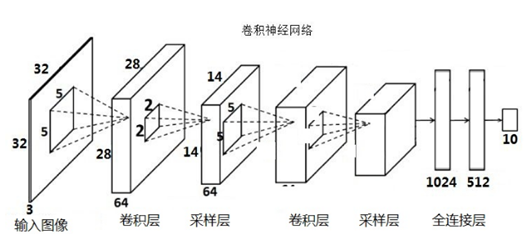
2、数据输入层:
l该层要做的处理主要是对原始图像数据进行预处理,其中包括:
• 去均值:把输入数据各个维度都中心化为0,如下图所示,其目的就是把样本的中心拉回到坐标系原点上。
• 归一化:幅度归一化到同样的范围,如下所示,即减少各维度数据取值范围的差异而带来的干扰,比如,我们有两个维度的特征A和B,A范围是0到10,而B范围是0到10000,如果直接使用这两个特征是有问题的,好的做法就是归一化,即A和B的数据都变为0到1的范围。
• PCA/白化:用PCA降维;白化是对数据各个特征轴上的幅度归一化
l 去均值与归一化效果图:

l 去相关与白化效果图:

3、卷积计算层
先介绍卷积层遇到的几个名词:
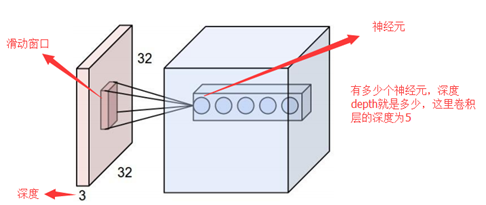
• 深度/depth(解释见下图)
• 步长/stride (窗口一次滑动的长度)
• 填充值/zero-padding
3.1、首先需要确定卷积核的形成:
我们先来回顾一下卷积公式:
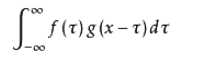
它的物理意义大概可以理解为:系统某一时刻的输出是由多个输入共同作用(叠加)的结果。
放在图像分析里,f(x) 可以理解为原始像素点(source pixel),所有的原始像素点叠加起来,就是原始图了。
g(x)可以称为作用点,所有作用点合起来我们称为卷积核(Convolution kernel)
卷积核上所有作用点依次作用于原始像素点后(即乘起来),线性叠加的输出结果,即是最终卷积的输出,也是我们想要的结果,我们称为destination pixel.
对于一维函数f(x),其一阶微分的基本定义是差值(对于离散函数,用差分来表示微分方程,![]() y除以
y除以![]() x,只是此时的
x,只是此时的![]() x为1,故微分方程可得下式):
x为1,故微分方程可得下式):
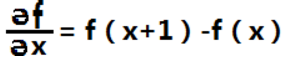
我们将二阶微分定义成如下差分:

我们首先我们来看边缘的灰度分布图以及将一二阶微分作用于边缘上:
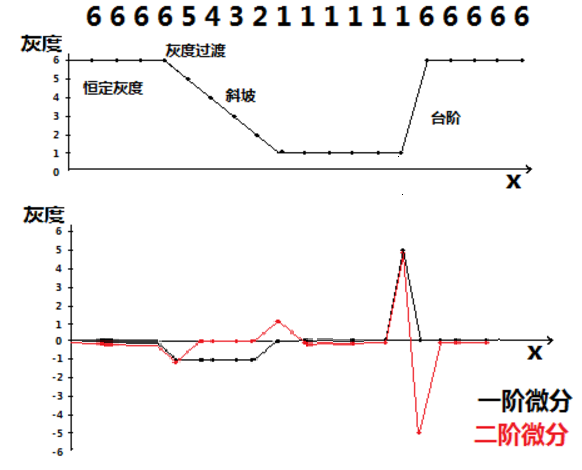
我们可以看到,在边缘(也就是台阶处),二阶微分值非常大,其他地方值比较小或者接近0 .
那我们就会得到一个结论,微分算子的响应程度与图像在用算子操作的这一点的突变程度成正比,这样,图像微分增强边缘和其他突变(如噪声),而削弱灰度变化缓慢的区域。
也就是说,微分算子(尤其是二阶微分),对边缘图像非常敏感。
很多时候,我们最关注的是一种各向同性的滤波器,这种滤波器的响应与滤波器作用的图像的突变方向无关。也就是说,各向同性滤波器是旋转不变的,即将原图像旋转之后进行滤波处理,与先对图像滤波再旋转的结果应该是相同的。
可以证明,最简单的各向同性微分算子是拉普拉斯算子。
一个二维图像函数f(x,y)的拉普拉斯算子定义为
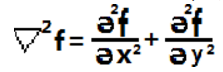
那么对于一个二维图像f(x,y),我们用如下方法去找到这个拉普拉斯算子:
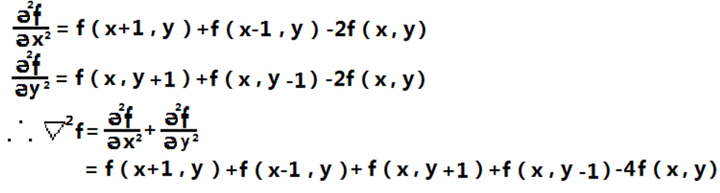
这个结果看起来太复杂,我们能不能用别的方式重新表达一下,如果我们以x,y 为坐标轴中心点,来重新表达这个算子,就可以是:
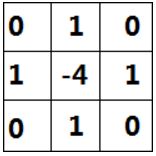
等等,这个是不是有点和上面提到的卷积核(Convolutional kernel)有点像了?
我们再回到拉普拉斯算子,
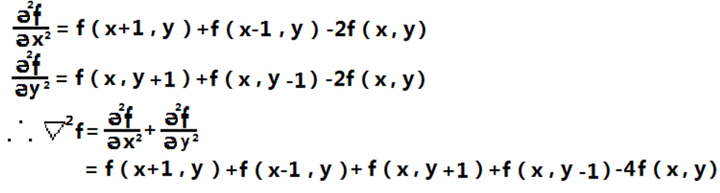
由于拉普拉斯是一种微分算子,因此其应用强调的是图像中的灰度突变。
将原图像和拉普拉斯图像叠加在一起,从而得到锐化后的结果。
于是模板就变为:
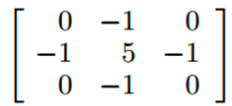
注:如果所使用的模板定义有负的中心系数,那么必须将原图像减去经拉普拉斯变换后的图像,而不是加上他。
上面这个,就是一个锐化卷积核模板了。原始边缘与它卷积,得到的就是强化了的边缘(destination pixel),图像变得更加锐利。
3.2、确定卷积核后再明确一下卷积的过程:
这一层就是卷积神经网络最重要的一个层次,也是“卷积神经网络”的名称来源,在这个卷基层,有两个关键操作:
• 局部关联:每个神经元看作一个滤波器(filter)
• 窗口(receptive field)滑动,filter对局部数据计算。
填充值是什么呢?以下图为例子,比如有这么一个5*5的图片(一个格子一个像素),我们滑动窗口取2*2,步长取2,那么我们发现还剩下1个像素没法滑完,那怎么办呢?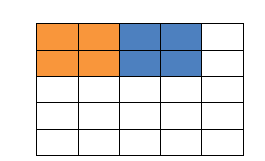
那我们在原先的矩阵加了一层填充值,使得变成6*6的矩阵,那么窗口就可以刚好把所有像素遍历完。这就是填充值的作用。
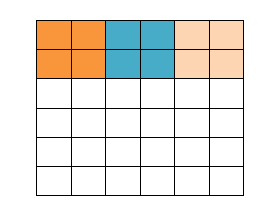
卷积的计算(注意,下面蓝色矩阵周围有一圈灰色的框,那些就是上面所说到的填充值)
在运算过程中,需要用到激活函数进行运算,常用的是:ReLU函数。

蓝色矩阵与粉色矩阵的sum运算完成后,会形成output volume矩阵,这个output volume矩阵是部分连接,即卷积之后加和的结果,进入下一层时还需要进行ReLU激活函数的运算。才可以进入池化层。
这里的蓝色矩阵就是输入的图像,粉色矩阵就是卷积层的神经元,这里表示了有两个神经元(w0,w1)。绿色矩阵就是经过卷积运算后的输出矩阵,这里的步长设置为2。
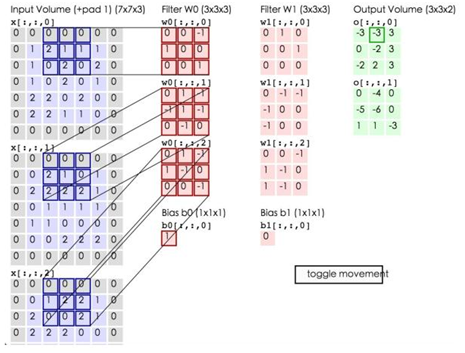
蓝色的矩阵(输入图像)对粉色的矩阵(filter)进行矩阵内积计算并将三个内积运算的结果与偏置值b相加(比如上面图的计算:2+(-2+1-2)+(1-2-2) + 1= 2 - 3 - 3 + 1 = -3),计算后的值就是绿框矩阵的一个元素。

参数共享机制
• 在卷积层中每个神经元连接数据窗的权重是固定的,每个神经元只关注一个特性。神经元就是图像处理中的滤波器,比如边缘检测专用的Sobel滤波器,即卷积层的每个滤波器都会有自己所关注一个图像特征,比如垂直边缘,水平边缘,颜色,纹理等等,这些所有神经元加起来就好比就是整张图像的特征提取器集合。
• 需要估算的权重个数减少: AlexNet 1亿 => 3.5w
• 一组固定的权重和不同窗口内数据做内积: 卷积

4、激励层计算:
将上一步的运算结果output volume矩阵用激励函数运算,并得到新的矩阵,这一个过程为激励层计算;
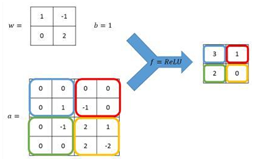
把卷积层输出结果做非线性映射,即通过ReLU函数等激励函数,将output volume矩阵转换成激励函数处理之后的矩阵,激励的方式为下图样式: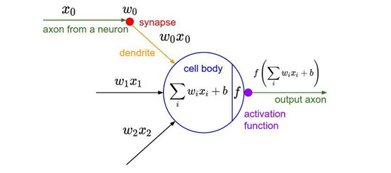
CNN采用的激励函数一般为ReLU(The Rectified Linear Unit/修正线性单元),它的特点是收敛快,求梯度简单,但较脆弱,图像如下。

x>0时,函数为:f(x)=x
x<=0时,函数为:f(x)=0
激励层的实践经验:
①不要用sigmoid!不要用sigmoid!不要用sigmoid!
② 首先试RELU,因为快,但要小心点
③ 如果2失效,请用Leaky ReLU或者Maxout
④ 某些情况下tanh倒是有不错的结果,但是很少
激励层与卷基层往往混合在一起,当卷积层将矩阵中的值与权重矩阵进行加和后,激励函数就会将其转化成激励之后的矩阵,激励层运算完成后,矩阵的维度不变。
5、池化层计算:
池化层夹在连续的卷积层中间, 用于压缩数据和参数的量,减小过拟合。
简而言之,如果输入是图像的话,那么池化层的最主要作用就是压缩图像。
这里再展开叙述池化层的具体作用。
1. 特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征。
2. 特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用。
3. 在一定程度上防止过拟合,更方便优化。
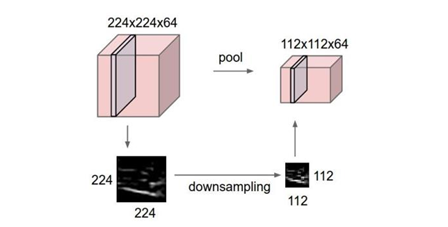
池化层用的方法有Max pooling 和 average pooling,而实际用的较多的是Max pooling。
这里就说一下Max pooling,其实思想非常简单。
对于每个2*2的窗口选出最大的数作为输出矩阵的相应元素的值,比如输入矩阵第一个2*2窗口中最大的数是6,那么输出矩阵的第一个元素就是6,如此类推。
6、全连接层计算:
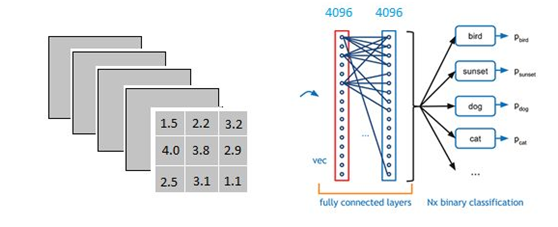
以上图为例,我们仔细看上图全连接层的结构,全连接层中的每一层是由许多神经元组成的(1x 4096)的平铺结构,上图不明显,我们看下图:

注:上图和我们要做的下面运算无联系
并且不考虑激活函数和bias。
当我第一次看到这个全连接层,我的第一个问题是:
它是怎么样把3x3x5的输出,转换成1x4096的形式。
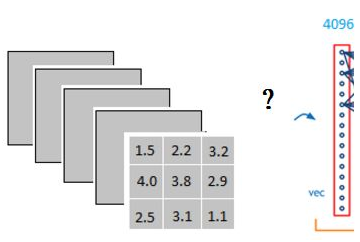
可以理解为在中间做了一个卷积:
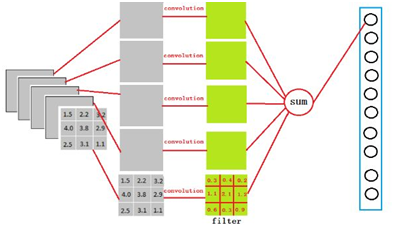
从上图我们可以看出,我们用一个3x3x5的filter 去卷积激活函数的输出,得到的结果就是一个fully connected layer 的一个神经元的输出,这个输出就是一个值。
因为我们有4096个神经元,我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出
以VGG-16再举个例子吧。
再VGG-16全连接层中,对224x224x3的输入,最后一层卷积可得输出为7x7x512,如后层是一层含4096个神经元的FC,则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程。
这一过程就是它把特征representation整合到一起,输出为一个值。
全连接层有两层1x4096fully connected layer平铺结构(有些网络结构有一层的,或者二层以上的),这样做的目的是为了解决非线性问题,就像是泰勒公式可以用多项式函数去拟合光滑函数。

我们这里的全连接层中一层的一个神经元就可以看成一个多项式,用许多神经元去拟合数据分布
但是只用一层fully connected layer 有时候没法解决非线性问题,而如果有两层或以上fully connected layer就可以很好地解决非线性问题了。
LeNet-5模型
LeNet-5模型是Yann LeCun教授于1998年在论文Gradient-based learning applied to document recognition中提出的,它是第一个成功应用于数字识别问题的卷积神经网络。在MNIST数据集上,LeNet-5模型可以达到大约99.2%的正确率。LeNet-5模型总共有7层,图7展示了LeNet-5模型的架构。
(点击放大图像)
图7 LeNet-5模型结构图。
在下面的篇幅中将详细介绍LeNet-5模型每一层的结构。论文GradientBased Learning Applied to Document Recognition提出的LeNet-5模型中,卷积层和池化层的实现与上文中介绍的TensorFlow的实现有细微的区别,这里不过多的讨论具体细节,而是着重介绍模型的整体框架。
第一层,卷积层
这一层的输入就是原始的图像像素,LeNet-5模型接受的输入层大小为32×32×1。第一个卷积层过滤器的尺寸为5×5,深度为6,不使用全0填充,步长为1。因为没有使用全0填充,所以这一层的输出的尺寸为32-5+1=28,深度为6。这一个卷积层总共有5×5×1×6+6=156个参数,其中6个为偏置项参数。因为下一层的节点矩阵有28×28×6=4704个节点,每个节点和5×5=25个当前层节点相连,所以本层卷积层总共有4704×(25+1)=122304个连接。
第二层,池化层
这一层的输入为第一层的输出,是一个28×28×6的节点矩阵。本层采用的过滤器大小为2×2,长和宽的步长均为2,所以本层的输出矩阵大小为14×14×6。原始的LeNet-5模型中使用的过滤器和本文中介绍的有些细微差别,这里不做具体介绍。
第三层,卷积层
本层的输入矩阵大小为14×14×6,使用的过滤器大小为5×5,深度为16。本层不使用全0填充,步长为1。本层的输出矩阵大小为10×10×16。按照标准的卷积层,本层应该有5×5×6×16+16=2416个参数,10×10×16×(25+1)=41600个连接。
第四层,池化层
本层的输入矩阵大小为10×10×16,采用的过滤器大小为2×2,步长为2。本层的输出矩阵大小为5×5×16。
第五层,全连接层
本层的输入矩阵大小为5×5×16,在LeNet-5模型的论文中将这一层称为卷积层,但是因为过滤器的大小就是5×5,所以和全连接层没有区别,在之后的TensorFlow程序实现中也会将这一层看成全连接层。如果将5×5×16矩阵中的节点拉成一个向量,那么这一层和在第四章中介绍的全连接层输入就一样了。本层的输出节点个数为120,总共有5×5×16×120+120=48120个参数。
第六层,全连接层
本层的输入节点个数为120个,输出节点个数为84个,总共参数为120×84+84=10164个。
第七层,全连接层
本层的输入节点个数为84个,输出节点个数为10个,总共参数为84×10+10=850个。
上面介绍了LeNet-5模型每一层结构和设置,下面给出一个TensorFlow的程序来实现一个类似LeNet-5模型的卷积神经网络来解决MNIST数字识别问题。通过TensorFlow训练卷积神经网络的过程和第五章中介绍的训练全连接神经网络是完全一样的。损失函数的计算、反向传播过程的实现都可以复用上一篇中给出的mnist_train.py程序。唯一的区别在于因为卷积神经网络的输入层为一个三维矩阵,所以需要调整一下输入数据的格式:
# 调整输入数据placeholder的格式,输入为一个四维矩阵。
x = tf.placeholder(tf.float32, [
BATCH_SIZE, # 第一维表示一个batch中样例的个数。
mnist_inference.IMAGE_SIZE, # 第二维和第三维表示图片的尺寸。
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS], # 第四维表示图片的深度,对于RBG格
#式的图片,深度为5。
name='x-input')
…
# 类似地将输入的训练数据格式调整为一个四维矩阵,并将这个调整后的数据传入sess.run过程。
reshaped_xs = np.reshape(xs, (BATCH_SIZE,
mnist_inference.IMAGE_SIZE,
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS))
在调整完输入格式之后,只需要在程序mnist_inference.py中实现类似LeNet-5模型结构的前向传播过程即可。下面给出了修改后的mnist_infernece.py程序。
# -*- coding: utf-8 -*-
import tensorflow as tf
# 配置神经网络的参数。
INPUT_NODE = 784
OUTPUT_NODE = 10
IMAGE_SIZE = 28
NUM_CHANNELS = 1
NUM_LABELS = 10
# 第一层卷积层的尺寸和深度。
CONV1_DEEP = 32
CONV1_SIZE = 5
# 第二层卷积层的尺寸和深度。
CONV2_DEEP = 64
CONV2_SIZE = 5
# 全连接层的节点个数。
FC_SIZE = 512
# 定义卷积神经网络的前向传播过程。这里添加了一个新的参数train,用于区分训练过程和测试
# 过程。在这个程序中将用到dropout方法,dropout可以进一步提升模型可靠性并防止过拟合,
# dropout过程只在训练时使用。
def inference(input_tensor, train, regularizer):
# 声明第一层卷积层的变量并实现前向传播过程。这个过程和6.3.1小节中介绍的一致。
# 通过使用不同的命名空间来隔离不同层的变量,这可以让每一层中的变量命名只需要
# 考虑在当前层的作用,而不需要担心重名的问题。和标准LeNet-5模型不大一样,这里
# 定义的卷积层输入为28×28×1的原始MNIST图片像素。因为卷积层中使用了全0填充,
# 所以输出为28×28×32的矩阵。
with tf.variable_scope('layer1-conv1'):
conv1_weights = tf.get_variable(
"weight", [CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_DEEP],
initializer=tf.truncated_normal_initializer(stddev=0.1))
conv1_biases = tf.get_variable(
"bias", [CONV1_DEEP], initializer=tf. constant_initializer(0.0))
# 使用边长为5,深度为32的过滤器,过滤器移动的步长为1,且使用全0填充。
conv1 = tf.nn.conv2d(
input_tensor, conv1_weights,
strides=[1, 1, 1, 1], padding='SAME')
relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))
# 实现第二层池化层的前向传播过程。这里选用最大池化层,池化层过滤器的边长为2,
# 使用全0填充且移动的步长为2。这一层的输入是上一层的输出,也就是28×28×32
# 的矩阵。输出为14×14×32的矩阵。
with tf.name_scope('layer2-pool1'):
pool1 = tf.nn.max_pool(
relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 声明第三层卷积层的变量并实现前向传播过程。这一层的输入为14×14×32的矩阵。
# 输出为14×14×64的矩阵。
with tf.variable_scope('layer3-conv2'):
conv2_weights = tf.get_variable(
"weight", [CONV2_SIZE, CONV2_SIZE, CONV1_DEEP, CONV2_DEEP],
initializer=tf.truncated_normal_initializer(stddev=0.1))
conv2_biases = tf.get_variable(
"bias", [CONV2_DEEP],
initializer=tf. constant_initializer(0.0))
# 使用边长为5,深度为64的过滤器,过滤器移动的步长为1,且使用全0填充。
conv2 = tf.nn.conv2d(
pool1, conv2_weights, strides=[1, 1, 1, 1], padding='SAME')
relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))
# 实现第四层池化层的前向传播过程。这一层和第二层的结构是一样的。这一层的输入为
# 14×14×64的矩阵,输出为7×7×64的矩阵。
with tf.name_scope('layer4-pool2'):
pool2 = tf.nn.max_pool(
relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 将第四层池化层的输出转化为第五层全连接层的输入格式。第四层的输出为7×7×64的矩阵,
# 然而第五层全连接层需要的输入格式为向量,所以在这里需要将这个7×7×64的矩阵拉直成一
# 个向量。pool2.get_shape函数可以得到第四层输出矩阵的维度而不需要手工计算。注意
# 因为每一层神经网络的输入输出都为一个batch的矩阵,所以这里得到的维度也包含了一个
# batch中数据的个数。
pool_shape = pool2.get_shape().as_list()
# 计算将矩阵拉直成向量之后的长度,这个长度就是矩阵长宽及深度的乘积。注意这里
# pool_shape[0]为一个batch中数据的个数。
nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
# 通过tf.reshape函数将第四层的输出变成一个batch的向量。
reshaped = tf.reshape(pool2, [pool_shape[0], nodes])
# 声明第五层全连接层的变量并实现前向传播过程。这一层的输入是拉直之后的一组向量,
# 向量长度为3136,输出是一组长度为512的向量。这一层和之前在第五章中介绍的基本
# 一致,唯一的区别就是引入了dropout的概念。dropout在训练时会随机将部分节点的
# 输出改为0。dropout可以避免过拟合问题,从而使得模型在测试数据上的效果更好。
# dropout一般只在全连接层而不是卷积层或者池化层使用。
with tf.variable_scope('layer5-fc1'):
fc1_weights = tf.get_variable(
"weight", [nodes, FC_SIZE],
initializer=tf.truncated_normal_initializer(stddev=0.1))
# 只有全连接层的权重需要加入正则化。
if regularizer != None:
tf.add_to_collection('losses', regularizer(fc1_weights))
fc1_biases = tf.get_variable(
"bias", [FC_SIZE], initializer=tf.constant_initializer(0.1))
fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_biases)
if train: fc1 = tf.nn.dropout(fc1, 0.5)
# 声明第六层全连接层的变量并实现前向传播过程。这一层的输入为一组长度为512的向量,
# 输出为一组长度为10的向量。这一层的输出通过Softmax之后就得到了最后的分类结果。
with tf.variable_scope('layer6-fc2'):
fc2_weights = tf.get_variable(
"weight", [FC_SIZE, NUM_LABELS],
initializer=tf.truncated_normal_initializer(stddev=0.1))
if regularizer != None:
tf.add_to_collection('losses', regularizer (fc2_weights))
fc2_biases = tf.get_variable(
"bias", [NUM_LABELS],
initializer=tf. constant_initializer(0.1))
logit = tf.matmul(fc1, fc2_weights) + fc2_biases
# 返回第六层的输出。
return logit
运行修改后的mnist_train.py和mnist_eval.py,可以得到一下测试结果:
~/mnist$ python mnist_train.py Extracting /tmp/data/train-images-idx3-ubyte.gz Extracting /tmp/data/train-labels-idx1-ubyte.gz Extracting /tmp/data/t10k-images-idx3-ubyte.gz Extracting /tmp/data/t10k-labels-idx1-ubyte.gz After 1 training step(s), loss on training batch is 6.45373. After 1001 training step(s), loss on training batch is 0.824825. After 2001 training step(s), loss on training batch is 0.646993. After 3001 training step(s), loss on training batch is 0.759975. After 4001 training step(s), loss on training batch is 0.68468. After 5001 training step(s), loss on training batch is 0.630368.
上面的程序可以将MNIST正确率达到~99.4%。
