【瞎口胡】计算几何基础

前言 / 鸣谢

计算几何是一种解决平面几何问题的神奇方法。

它的奇妙之处在于使用向量积可以减少许多分类讨论。基本上，当你随便选出一种情况讨论出答案之后，这个答案就可以适用于所有情况。

如果你还不知道笛卡尔坐标系（平面直角坐标系）和向量，我建议你现在就去学习它们。

本篇部分内容出自 wjyyy 的计算几何博客 和 辰星凌的计算几何博客，在这里感谢他们详细、优质的讲解。

准备工作

• 一些减少常数的 define 和 typedef

  # define Vector Point // 向量和点都可以只记录 (x,y)，因此它们共用一个结构体，但是阅读时需要区分
  # define DB double // 如果精度有要求可以替换为 long double
  # define CP const Point // 减少代码长度
  # define CV const Vector
  

• 常数

  const DB eps=1e-8; // 即当两个浮点数差的绝对值 < eps 时，认为它们相等
                     // 1e-8 是一个常用的值，可以根据精度要求调大调小
  const DB Pi=acos(-1); // 圆周率
  

• 存储点 / 向量

  使用一个结构体存储。

  struct Point{
  	DB x,y;
  	Point(DB X=0,DB Y=0){
  		x=X,y=Y;
  		return;
  	}
  };
  

  内置构造函数。这样可以方便地使用 Point(a,b) 这样的语法来创建一个坐标为 \((a,b)\) 的点。

  当然，向量和点的存储并没有区别，因此我们不需要额外地新建一个结构体 Vector 来存储它们。

• 存储直线

  存储直线上不重合的两点。

• 存储多边形

  使用 std::vector<Point>。为了方便起见，应该按照逆时针顺序存储。

基础操作

浮点数符号判断、浮点数绝对值

浮点数在运算的过程中会丢失精度。当一个数的绝对值小于 \(\operatorname{eps}\) 时，我们认为它等于 \(0\)。

我们同时可以得到求浮点数绝对值的方法：符号乘以原值。

inline int Sign(DB x){
	return (x<-eps)?-1:((x>eps)?1:0);
}
inline DB Fabs(DB x){
	return x*Sign(x);
}

向量加减、数乘

\[(x_1,y_1)\pm (x_2,y_2) = (x_1 \pm y_1,x_2 \pm y_2) \]

\(\lambda (x,y)= (\lambda x, \lambda y)\)

其中 \(\lambda \in \mathbb R\)。

Vector operator - (CV &u,CV &v){
	return Vector(u.x-v.x,u.y-v.y);
}
Vector operator + (CV &u,CV &v){
	return Vector(u.x+v.x,u.y+v.y);
}
Vector operator * (CV &u,DB k){
	return Vector(u.x*k,u.y*k);
}

向量判等 / 点判等

记住：尽量避免两个浮点数直接比较。

bool operator == (CP &u,CP &v){
	return !(Sign(u.x-v.x)||Sign(u.y-v.y)); 
} 

向量点积

向量的点积是一个数。\((x_1,y_1) \cdot (x_2,y_2) = x_1x_2 + y_1y_2\)。点积具有交换律。

想要记住这个式子，只需要明白，「点积」即对位相乘再求和。

\(\vec a \cdot \vec b\) 的几何意义是 \(\vec a\) 在 \(\vec b\) 方向上的投影乘以 \(\vec b\) 的模长。

图片来源于网络。

何为「投影」？将 \(\vec a,\vec b\) 平移到同一起点 \(O\)，过 \(\vec b\) 的终点作 \(\vec a\) 所在直线的垂线，设垂足为 \(P\)，有向线段 \(OP\) 即为 \(\vec b\) 在 \(\vec a\) 方向上的投影，即 \(a_0\)。

再次提醒 \(OP\) 是有向的，因此如果 \(P\) 在 \(O\) 左侧，投影长度会是一个负数。

根据三角函数的定义，有 \(\vec a \cdot \vec b = |\vec a||a_0| = |\vec a||\vec b| \cos \theta\)。事实上，这才是向量点积的原始定义。利用点积的两个公式可以方便地计算两个向量之间的夹角 \(\theta\)。从点积具有交换律这一事实容易得知，这里的 \(\theta\) 是无向的角，不区分是 \(\vec a\) 转向 \(\vec b\) 形成的角或是相反。

夹角与点积大小的关系：

• 若 \(\theta = 0^\circ\)，则 \(\vec a \cdot \vec b = |\vec a||\vec b|\)。
• 若 \(0^\circ <\theta < 90^\circ,\vec a \cdot \vec b > 0\)。
• 若 \(\theta = 90^\circ,\vec a \cdot \vec b = 0\)。
• 若 \(90^\circ <\theta < 180^\circ,\vec a \cdot \vec b < 0\)。
• 若 \(\theta = 180^\circ\)，则 \(\vec a \cdot \vec b =- |\vec a||\vec b|\)。

inline DB Dot(CV &u,CV &v){
	return u.x*v.x+u.y*v.y;
}

向量叉积

\((x_1,y_1) \times (x_2,y_2) = x_1y_2 - x_2y_1\)。叉积不具有交换律。

叉积的几何意义是 \(\vec a\) 转动一个不超过 \(180^\circ\) 的有向角 \(\theta\) 转到 \(\vec b\) 形成的有向平行四边形面积。如果 \(\theta > 0^\circ\)，那么面积为正，否则面积为负。特别的，当 \(\theta = 0 ^\circ\) 或 \(\theta = 180^\circ\) 时，面积为 \(0\)。

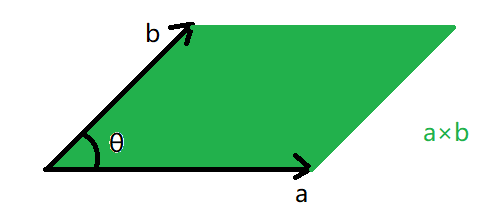
一个 \(\theta\) 为正的例子。

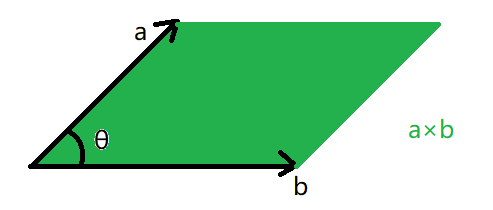
一个 \(\theta\) 为负的例子。

向量叉积一个简单而有趣的应用是求两个向量围成的三角形的面积。只需要将叉积的结果除以 \(2\) 就行，但这个应用非常重要！

inline DB Cro(CV &u,CV &v){
	return u.x*v.y-u.y*v.x;
}

向量积的小结

向量点积可以用来判断向量间的前后关系。

向量叉积可以用来判断向量间的左右关系。

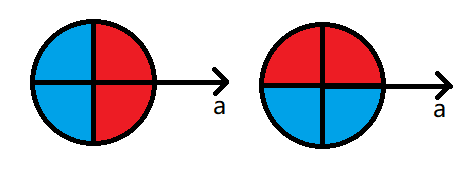
将两个向量 \(\vec a,\vec b\) 平移到同一起点（图中圆心），那么点积为正当且仅当 \(\vec b\) 经过图左中红色部分，即 \(\vec a,\vec b\) 均「朝向前方」。

叉积为正当且仅当 \(\vec b\) 经过左图中红色部分，即 \(\vec b\) 在 \(\vec a\) 左侧。

为了方便作图，这里只展示了 \(\vec a\) 平行于 \(x\) 轴且方向为正的情况。对于其它情况，可以旋转坐标系得到同样的结论。

点的旋转

将 \(P(x,y)\) 绕原点顺时针旋转角度 \(\theta\)（如果要逆时针旋转 \(\theta\) ，顺时针旋转 \(2\pi - \theta\) 即可）之后，\(P\) 点坐标变为 \((x \cos \theta + y \sin \theta,-x \sin \theta + y \cos \theta)\)。

这同样很好记忆。只需要将 \(x\) 坐标的变化进行三处取反（所有的 \(\sin,\cos\) 互换，\(x\) 变为 \(-x\)）就可以得到 \(y\) 坐标的变换。

如果指定旋转中心，可以把原点搬到旋转中心去，这样就和上面的做法相差无几。

因此，\(P(x,y)\) 绕 \(C(x_0,y_0)\) 顺时针旋转角度 \(\theta\) 后坐标变为 \(((x-x_0) \cos \theta + (y-y_0) \sin \theta,-(x-x_0) \sin \theta + (y-y_0) \cos \theta)\)。

inline Point PointTurn(CP &u,DB theta){
	return Point(u.x*cos(theta)+u.y*sin(theta),-u.x*sin(theta)+u.y*cos(theta));
}
inline Point PointTurn(CP &u,DB theta,CP &c){
	return Point((u.x-c.x)*cos(theta)+(u.y-c.y)*sin(theta)+c.x,-(u.x-c.x)*sin(theta)+(u.y-c.y)*cos(theta)+c.y);
}
// 函数重载，便于阅读

点与线的操作

判断点是否在直线上

对于点 \(P\) 和直线 \(AB\)，作向量 \(\vec{AP}\) 和 \(\vec{BP}\)，如果 \(P\) 在 \(AB\) 上，那么它们应该共线（叉积为 \(0\)）。

inline bool PointonLine(CP &u,CP &a,CP &b){
	return !Sign(Cro(u-a,u-b));
}

判断点是否在线段上

这比在直线上的判断更加严格。事实上，我们还需要额外判断 \(\vec{AP}\) 和 \(\vec{BP}\) 是否反向。原因非常显然。

inline bool PointonSeg(CP &u,CP &a,CP &b){
	return !Sign(Cro(u-a,u-b))&&(Dot(u-a,u-b)<=0);
}

点到直线的距离

对于点 \(P\) 和直线 \(AB\)，作向量 \(\vec{AP},\vec{AB}\)，则 \(P\) 到 \(AB\) 的距离为 \(\left|\dfrac{\vec{AB} \times \vec{AP}}{|\vec{AB}|}\right|\)，即平行四边形面积除以底边长，其中外层符号表示绝对值，因为叉积是有向的。

点到线段的距离

如果线段退化成点，则点到线段的距离即两点距离，作向量求模长即可。

我们发现，求点到线段的距离和直线不同的是，\(P\) 在一些特殊位置时，最优解是直接走到线段的某个端点。

那么这些特殊位置是？直观上，它们就是超出这个线段「范围」的点。

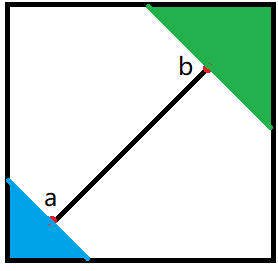
如图，在蓝色部分的点只需要走到端点 \(A\)，在绿色部分的点只需要走到端点 \(B\)。我们惊喜地发现，蓝色部分的边界是过 \(A\) 点的一条 \(AB\) 垂线，绿色部分同理。

于是我们只需要分别作向量 \(\vec{AP}\)，\(\vec{BP}\) 和 \(\vec{AB}\)，然后依次判断：

• \(\vec{AP} \cdot \vec{AB}\) 的点积是否小于 \(0\)。如果小于 \(0\)，那么 \(P\) 在蓝色区域。
• \(\vec{BP} \cdot \vec{AB}\) 的点积是否大于 \(0\)。如果大于 \(0\)，那么 \(P\) 在绿色区域。
• 如果上述条件不满足，则 \(P\) 在线段的「范围」中，即白色区域或线段上。

inline bool DistoSeg(CP &u,CP &a,CP &b){
	if(a==b)
		return Len(u-a);
	Vector au=u-a,bu=u-b,ab=b-a;
	if(Sign(Dot(au,ab))<0)
		return Len(au);
	if(Sign(Dot(bu,ab))>0)
		return Len(bu);
	return Fabs(Cro(au,ab)/Len(ab));
}

点到直线的垂足

对于点 \(P\) 和直线 \(AB\)，计算出 \(\vec{AP}\) 在 \(\vec{AB}\) 方向上的投影长度，然后数乘一下即可。

inline Point FootPoint(CP &u,CP &a,CP &b){
	Vector au=u-a,bu=u-b,ab=b-a;
	DB aulen=Dot(au,ab)/Len(ab),bulen=-1.0*Dot(bu,ab)/Len(ab);
	return a+ab*(aulen/(aulen+bulen)); // 理论上这里 aulen + bulen 也应该和向量 AB 模长相等
    // 不知道作者有什么奇妙用意
}

点关于直线的对称点

算出垂足然后倍长向量。

inline Point SymPoint(CP &u,CP &a,CP &b){
	return u+(FootPoint(u,a,b)-u)*2;
}

线与线的操作

求两直线交点

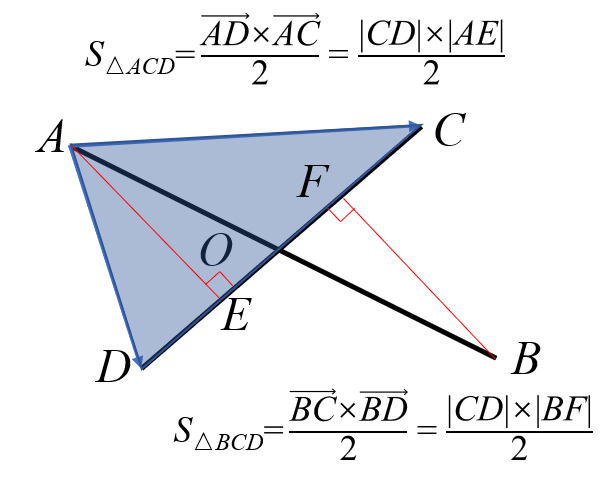
如上图，对于两直线 \(AB,CD\)，我们只需要算出 \(AO\) 和 \(AB\) 的比值（或者等价地算出 \(\dfrac{AO}{AB}\) 的比值）\(k\) 就可以用 \(A+k\vec{AB}\) 来计算出点 \(O\) 的坐标。事实上，\(\dfrac{AO}{OB} = \dfrac{AE}{FB} = \frac{S_{\bigtriangleup ACD}}{S_{\bigtriangleup BCD}}\)。

另外，\(\vec{AB} \times \vec{CD}\) 可以计算出四边形 \(ACBD\) 的面积的两倍。因为将 \(\vec{AB}\) 平移到和 \(\vec{CD}\) 同一起点后，叉积形成的平行四边形底（\(CD\)）不变，高也不变（考虑将 \(AE\)，\(FB\) 和 \(AB\) 作同步平移），所以它们面积相等。

于是 \(\dfrac{\vec{CD}\times \vec{CA}}{\vec{AB} \times \vec{CD}}\) 就是 \(\vec{AO}\) 模长和 \(\vec{AB}\) 模长的比值。不需要担心符号问题，前人已经为我们证明过了...在初学的时候还是先直观感性理解比较合适。

inline Point CrossLL(CP &a,CP &b,CP &c,CP &d){
	Vector ab=b-a,cd=d-c,ca=a-c;
	return a+ab*(Cro(cd,ca)/Cro(ab,cd));
}

判断线段和直线是否有交

即判断该线段所在直线和另一直线的交点是否在该线段上。

inline bool CrossLS(CP &a,CP &b,CP &c,CP &d){ // Line AB and Segment CD
	return (PointonLine(CrossLL(a,b,c,d),c,d));
}

判断两线段是否严格相交

严格相交指：交点不在端点处。

我们使用跨立实验。即：当两线段 \(AB,CD\) 满足：

• \(A,B\) 分别位于直线 \(CD\) 的两侧
• \(C,D\) 分别位于直线 \(AB\) 的两侧

时，我们认为它们相交。

用叉积简单判断。

inline bool CrossSS(CP &a,CP &b,CP &c,CP &d){
	DB ab_c=Cro(b-a,c-a),ab_d=Cro(b-a,d-a);
	DB cd_a=Cro(d-c,a-c),cd_b=Cro(d-c,b-c);
	return (Sign(ab_c)*Sign(ab_d)<0)&&(Sign(cd_a)*Sign(cd_b)<0);
}

如果允许它们在端点处相交（不严格相交），可以额外算出两直线交点，然后和四个端点判等。只要和四个端点之一相等或者上面的函数返回值为 true，我们就认为它们不严格相交。

多边形

三角剖分求任意多边形面积

前文提到过，我们逆时针存储多边形。有结论，对于 \(n\) 个点的多边形 \(P=\{P_1,P_2,\cdots,P_n\}\)，其面积为 \(\sum \limits_{i=2}^{n} P_{i-1} \times P_i + P_n \times P_1\)（此时 \(P_i\) 看作向量）。计算过程如图所示（红色为负，蓝色为正）。

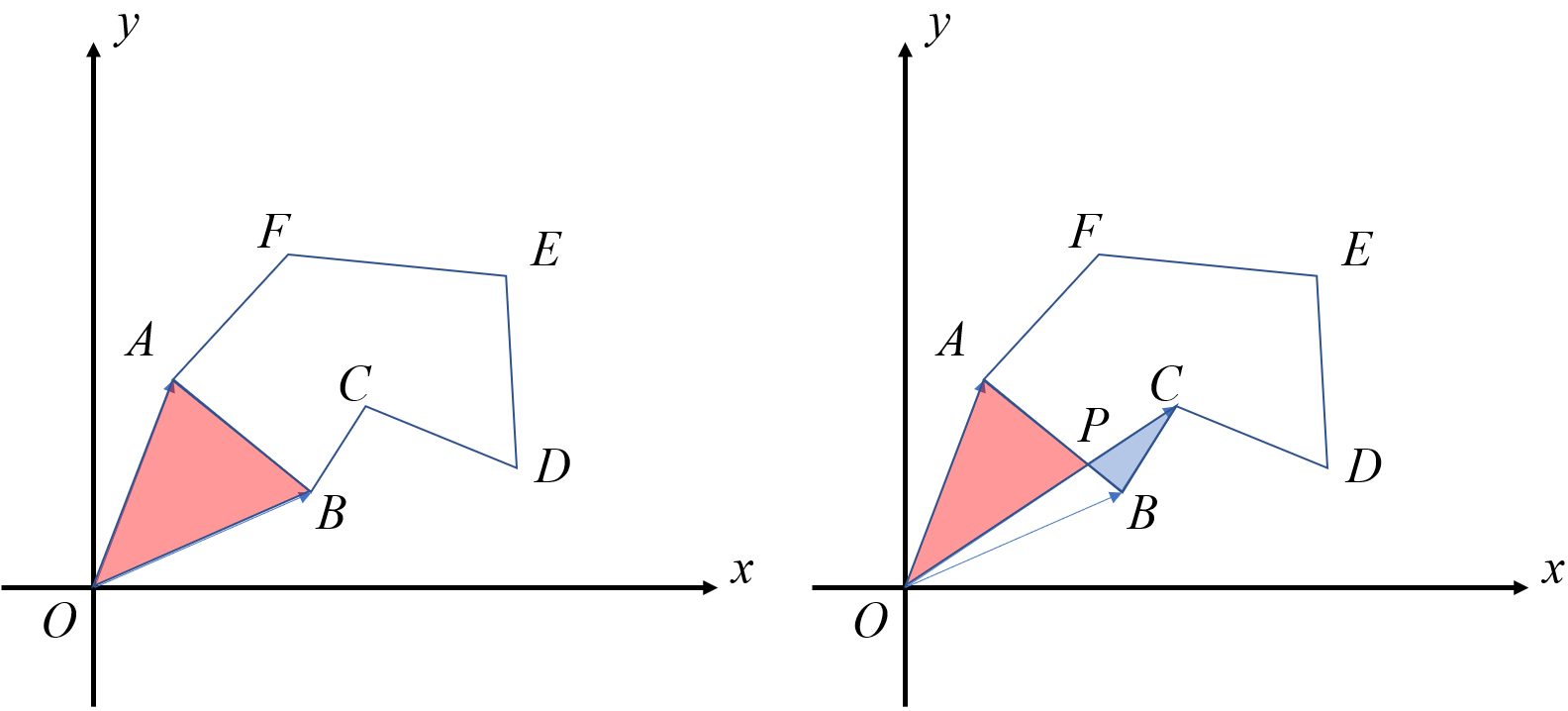
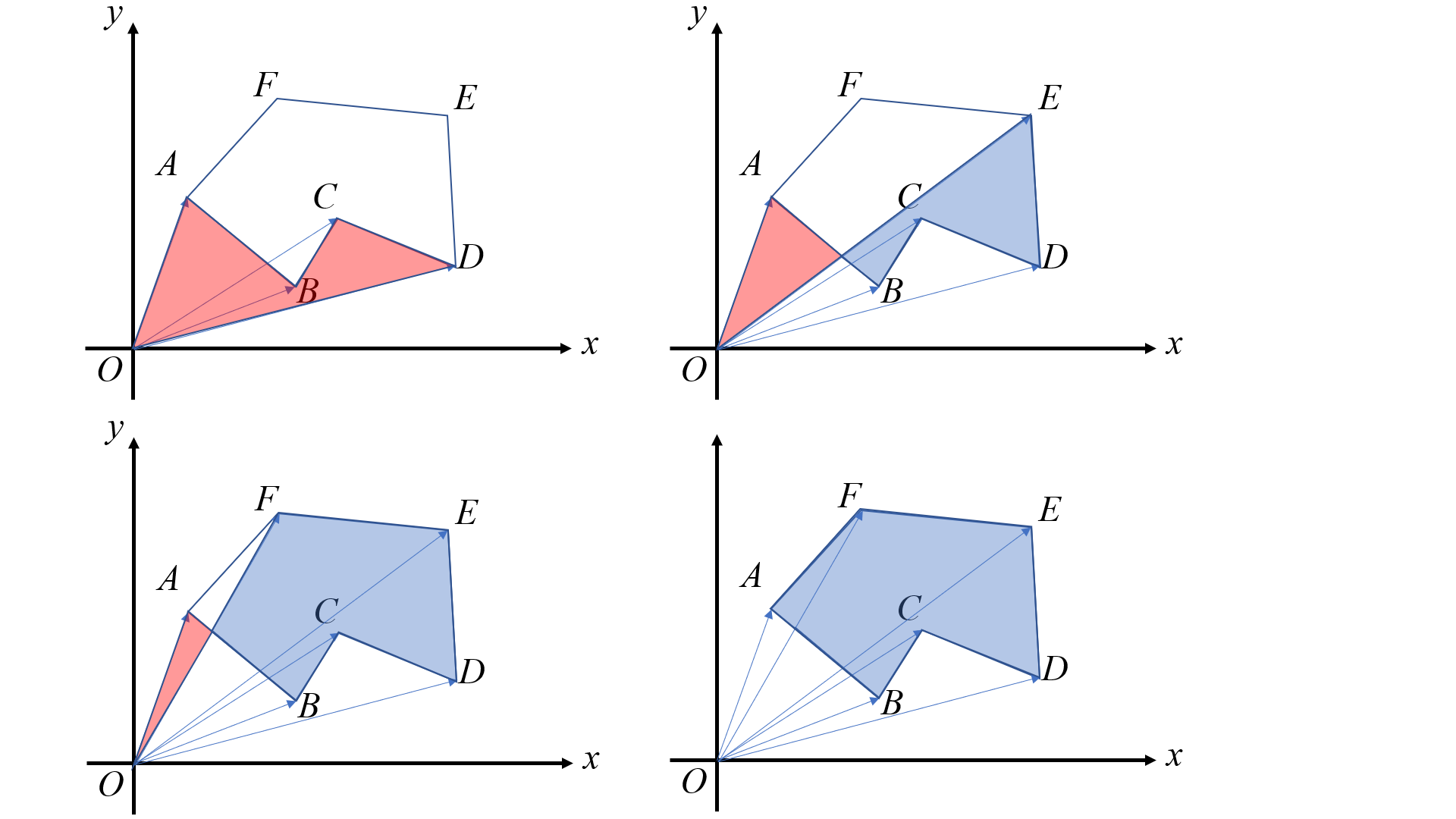
inline DB PolyArea(Poly &P){
	DB res=0;
	for(int i=0;i<(int)P.size();++i){
		res+=Cro(P[i],P[(i+1)%P.size()]);
	}
	return res/2.0; // 时刻记得叉积其实求的是平行四边形面积
}

求凸包

对于平面上的 \(n\) 个点 \(P_1,P_2,\cdots,P_n\)，将其按照 \(x,y\) 坐标进行双关键字排序，取前两个点加入凸包。首先排序后的第一个点一定在凸包里，然后看新加入的点：

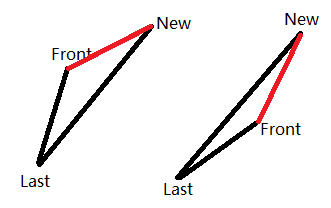
如果是左图中的情况，直接把它加进去就行。如果是右图中的情况，现在凸包中最后一个点没啥用了，应该删掉。

于是加点的决策就是不停删点直到凸包只有一个点了或者出现情况一为止。

用向量旋转来说的话就是向量 \(\vec{LF}\) 落到了 \(\vec{LN}\) 的左侧就是情况一。注意共线的情况。

做完了一遍会得到一个上凸壳，反着遍历点再做一遍就可以得到下凸壳，从而合并成一个完整凸包。

inline void ConvexHull(Poly &P,Poly &ans){
	int n=P.size();
	std::sort(P.begin(),P.end(),x_comp);
	ans.resize(0);
	int siz=0;
	for(int i=0;i<n;++i){
		while(siz>1&&Sign(Cro(ans[siz-1]-ans[siz-2],P[i]-ans[siz-2]))<=0) // not < 
			--siz,ans.pop_back();
		ans.push_back(P[i]),++siz;
	}
	for(int i=n-1,st=siz;i>=0;--i){
		while(siz>st&&Sign(Cro(ans[siz-1]-ans[siz-2],P[i]-ans[siz-2]))<=0)
			--siz,ans.pop_back();
		ans.push_back(P[i]),++siz;
	}
	ans.pop_back();
	return;
}

旋转卡壳

逆时针枚举一条边，离这条边最远的点也会逆时针移动。叉积判断一下距离是否增加即可。

网上有讲详细证明。

inline DB PolyDiameter(Poly &P){
	int n=P.size();
	if(P.size()<2)
		return 0;
	if(P.size()==2)
		return Len(P[0]-P[1]);
	int now=2;
	DB res=0;
	P.push_back(P[0]);
	for(int i=0;i<n;++i){
		while(Sign(Cro(P[i+1]-P[i],P[now]-P[i])-Cro(P[i+1]-P[i],P[now+1]-P[i]))<0)
			now=(now+1)%n;
		res=std::max(res,std::max(Len(P[now]-P[i]),Len(P[i+1]-P[i])));
	}
	P.pop_back();
	return res;
}