一次生日Party可能有p人或者q人参加,现准备有一个大蛋糕.问最少要将蛋糕切成多少块(每块大小不一定相等),才能使p人或者q人出席的任何一种情况,都能平均将蛋糕分食.
Input
每行有两个数p和q.Output
输出最少要将蛋糕切成多少块.
Sample Input
2 3
Sample Output
4
Hint
将蛋糕切成大小分别为1/3,1/3,1/6,1/6的四块即满足要求.
当2个人来时,每人可以吃1/3+1/6=1/2 , 1/2块。
当3个人来时,每人可以吃1/6+1/6=1/3 , 1/3, 1/3块。Author
LLSource
HZIEE 2007 Programming ContestRecommend
lcy
这道题一开始看就懵逼了,无论怎么生拉硬扯都怎么推构造不出一个规律或公式来,只好搜题解。
这才想明白了(转载自http://blog.csdn.net/zy691357966/article/details/39699945,有部分修改)。
一开始用代数思维思考 发现十分麻烦
想到用图像去解释 如下图
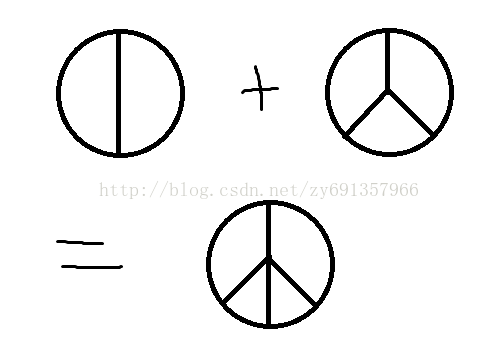
题目就转换为 p+q-k k为先按p,q平均分 合成后的时候有多少公共边 (必定一条边先对齐)
题目就转换为 p+q-k k为先按p,q平均分 合成后的时候有多少公共边 (必定一条边先对齐)
即求
k1(360/p)=k2(360/q) 0=<k1<p 0=<k2<q;
满足条件的k1,k2组数
由于k1,k2,p,q 都要求是正整数,很明显,有GCD(q,p) 组解
所以,最小的切数为 p+q-GCD(p,q)