1631. 最小体力消耗路径
Difficulty: 中等
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小** 体力消耗值** 。
示例 1:
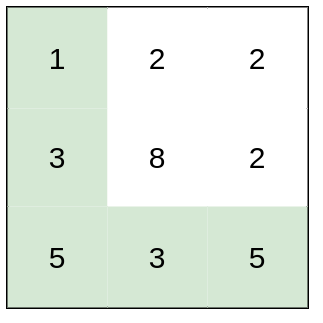
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
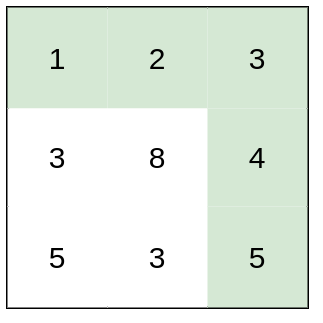
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
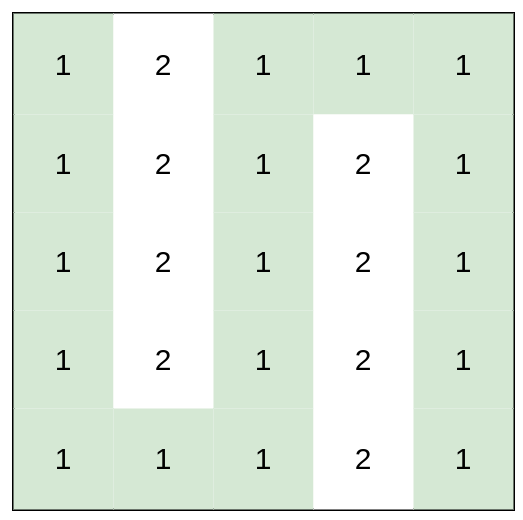
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 10<sup>6</sup>
Solution
思路:查找一条路径使该路径代价最小,路径的代价为该路径上最大权的边。首先题目给的是点的信息,需要先将它转化为图,将二维地图的每一个格视为一个点,相邻的格之间有边相连,边权值为两个格的数值差。
一般我们只要深度遍历或广度遍历图结点计算所有路径的代价即可,但图中点一多就很容易超时,因此,我们转化思路,只要找到一条路径使它从起始点到出发点的代价最小就行,那么我们只要从权重最小的边开始找,当该条边加入图中时能使起点到终点连通,那么该边权重,就是所在路径的代价,也就是要找的结果。
所以,使用并查集判断图是否连通。当一条边加入图中后,起点到终点连通,而且该边的权重为图中最大权值,所以它就是要找的答案。
Language: java
class Solution {
public int minimumEffortPath(int[][] heights) {
int l = heights.length;
int w = heights[0].length;
int[][] edges = new int[2*l*w-l-w][3];
int idx = 0;
for(int i=0; i<l; i++){
for(int j=0; j<w; j++) {
if (j > 0) {
edges[idx][0] = i*w+j-1;
edges[idx][1] = i*w+j;
edges[idx++][2] = Math.abs(heights[i][j - 1] - heights[i][j]);
}
if (i > 0) {
edges[idx][0] = i*w+j-w;
edges[idx][1] = i*w+j;
edges[idx++][2] = Math.abs(heights[i - 1][j] - heights[i][j]);
}
}
}
Arrays.sort(edges, Comparator.comparingInt(a -> a[2]));
UnionFind uf = new UnionFind(l*w);
int res = 0;
for(int i=0; i<edges.length; i++){
uf.merge(edges[i][0], edges[i][1]);
if(uf.find(0) == uf.find(l*w-1)){
res = edges[i][2];
break;
}
}
return res;
}
class UnionFind{
int[] parent;
public UnionFind(int len){
parent = new int[len];
for(int i=0; i<len; i++) parent[i] = i;
}
public int find(int x){
return parent[x] == x ? x : (parent[x] = find(parent[x]));
}
public void merge(int x, int y){
parent[find(y)] = find(x);
}
}
}