Wall

题目大意：给N个点，然后要修建一个围墙把所有的点都包裹起来，但是要求围墙距离所有的点的最小距离是L，求出来围墙的长度。

分析：如果没有最小距离这个条件那么很容易看出来是一个凸包，然后在加上一个最小距离L，那么就是在凸包外延伸长度为L，如下图，很明显可以看出来多出来的长度就是半径为L的圆的周长，所以总长度就是凸包的周长+半径为L的圆的周长。

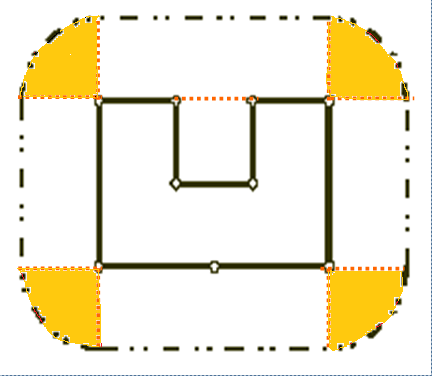
代码如下：

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<string>
#include<vector>
#include<math.h>
using namespace std;

const double EPS = 1e-10;
const double PI = acos(-1);
const int MAXN = 1e3+7;
int sta[MAXN], top;
int Sign(double t)
{
    if(t > EPS)return 1;
    if(fabs(t) < EPS)return 0;
    return -1;
}
struct point
{
    double x, y;
    point(double x=0, double y=0):x(x), y(y){}
    point operator - (const point &t)const{
        return point(x-t.x, y-t.y);
    }
    double operator ^(const point &t)const{
        return x*t.y - y*t.x;
    }
    double operator *(const point &t)const{
        return x*t.x + y*t.y;
    }
}p[MAXN];
double Dist(point a, point b)
{
    return sqrt((a-b)*(a-b));
}
bool cmp(point a, point b)
{
    int t = Sign((a-p[0])^(b-p[0]));

    if(t == 0)
        return Dist(a, p[0]) < Dist(b, p[0]);
    return t > 0;
}
///求凸包
void Graham(int N)
{///注意是否有1和2的情况，这个题目要求的
    sta[0]=0, sta[1]=1, top=1;

    for(int i=2; i<N; i++)
    {
        while(top>0 && Sign((p[i]-p[sta[top]])^(p[sta[top-1]]-p[sta[top]])) <= 0)
            top--;
        sta[++top] = i;
    }
}

int main()
{
    int N, L;

    while(scanf("%d%d", &N, &L) != EOF)
    {
        int i, k=0;

        for(i=0; i<N; i++)
        {
            scanf("%lf%lf", &p[i].x, &p[i].y);
            if(p[k].y>p[i].y || (p[k].y==p[i].y && p[k].x>p[i].x))
                k = i;
        }
        swap(p[0], p[k]);
        sort(p+1, p+N, cmp);
        Graham(N);

        double ans = Dist(p[sta[0]],p[sta[top]]) + 2*PI*L;

        for(int i=0; i<top; i++)
            ans += Dist(p[sta[i]], p[sta[i+1]]);

        printf("%d
", (int)(ans+0.5));
    }

    return 0;
}