一直不知道差分约束是什么类型题目,最近在写最短路问题就顺带看了下,原来就是给出一些形如x-y<=b不等式的约束,问你是否满足有解的问题
好神奇的是这类问题竟然可以转换成图论里的最短路径问题,下面开始详细介绍下
比如给出三个不等式,b-a<=k1,c-b<=
k2,c-a<=k3,求出c-a的最大值,我们可以把a,b,c转换成三个点,k1,k2,k3是边上的权,如图
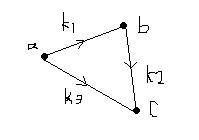
由题我们可以得知,这个有向图中,由题b-a<=k1,c-b<=k2,得出c-a<=k1+k2,因此比较k1+k2和k3的大小,求出最小的就是c-a的最大值了
根据以上的解法,我们可能会猜到求解过程实际就是求从a到c的最短路径,没错的....简单的说就是从a到c沿着某条路径后把所有权值和k求出就是c -a<=k的一个
推广的不等式约束,既然这样,满足题目的肯定是最小的k,也就是从a到c最短距离...
理解了这里之后,想做题还是比较有困难的,因为题目需要变形一下,不能单纯的算..
首先以poj3159为例,这个比较简单,就是给出两个点的最大差,然后让你求1到n的最大差,直接建图后用bellman或者spfa就可以过了
稍微难点的就是poj1364,因为他给出的不等式不是x-y<=k形式,有时候是大于号,这样需要我们去变形一下,并且给出的还是>,<没有等于,都要变形
再有就是poj1201,他要求出的是最长距离,那就要把形式变换成x-y>=k的标准形式
注意点:
1. 如果要求最大值想办法把每个不等式变为标准x-y<=k的形式,然后建立一条从y到x权值为k的边,变得时候注意x-y<k =>x-y<=k-1
如果要求最小值的话,变为x-y>=k的标准形式,然后建立一条从y到x的k边,求出最长路径即可
2.如果权值为正,用dj,spfa,bellman都可以,如果为负不能用dj,并且需要判断是否有负环,有的话就不存在
/////////////////////////////////////////////////////////////////////
队列会超时死,用栈就会过.....不要问为什么。。。。。。。为什么。。什么。。。么。。
#include<stack>
#include<stdio.h>
#include<string.h>
#include<string>
#include<map>
#include<iostream>
using namespace std;
const int maxn = 30005;
const int oo = 0x3fffffff;
struct node
{
int u, v, c, next;
}e[maxn*10];
int head[maxn], dis[maxn];
bool use[maxn];
void AddAge(int u, int v, int c, int k)
{
e[k].u = u;
e[k].v = v;
e[k].c = c;
e[k].next = head[u];
head[u] = k;
}
void spfaStack()
{
stack<int> sta;
sta.push(1);
while(sta.size())
{
int i = sta.top();sta.pop();
use[i] = false;
for(int j=head[i]; j != 0; j=e[j].next)
{
int u = e[j].u, v = e[j].v, c = e[j].c;
if(dis[v] > dis[u]+c)
{
dis[v] = dis[u]+c;
if(use[v] == false)
{
use[v] = true;
sta.push(v);
}
}
}
}
}
int main()
{
int N, M;
while(scanf("%d%d", &N, &M) != EOF)
{
int i, u, v, c;
for(i=1; i<=N; i++)
dis[i] = oo, head[i]=0;
dis[1] = 0;
for(i=1; i<=M; i++)
{
scanf("%d%d%d", &u, &v, &c);
AddAge(u, v, c, i);
}
spfaStack();
printf("%d ", dis[N]);
}
return 0;
}