1. 基本思想
- 插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
- 把 n 个待排序的元素看成为一个〈有序表〉和一个〈无序表〉,开始时有序表中只包含一个元素,无序表中包含有 n-1 个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它 插入到有序表中的适当位置,使之成为新的有序表。
2. 标配
- 平均时间复杂度:O(n^2)
- 最坏时间复杂度:O(n^2)
- 最好时间复杂度:O(n)
- 空间复杂度:O(1)
- 稳定
3. 两种方式
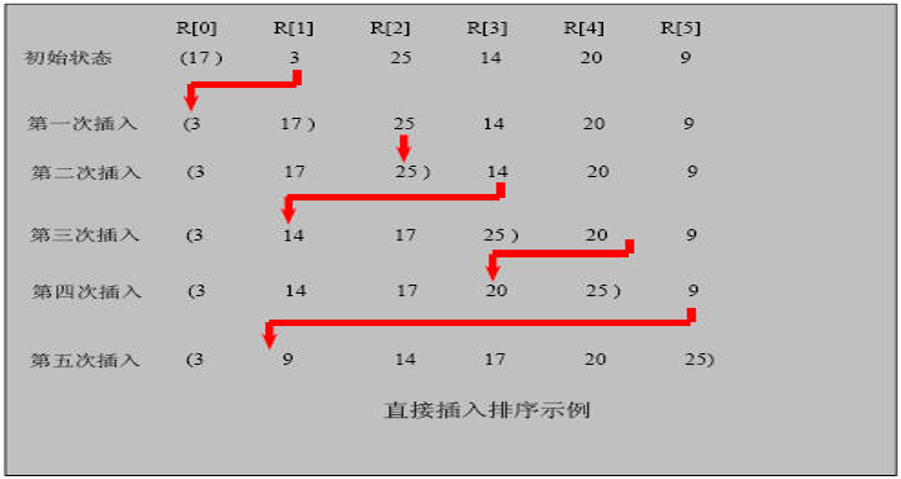
给「待插入元素」找位置的方法:
- PlanA (移位):先把「待插入元素」保存起来,然后从「待插入元素」前边一个元素 (即有序表尾元素)开始,往前遍历,凡是比 [待插入元素] 大的都先往后挪,最终腾出来的地儿再放置「待插入元素」。
- PlanB (交换):无需保存「待插入元素」,而是直接与「待插入元素」前边一个元素比较大小,要是前边一个比它大,就交换位置,再继续往前,直到「待插入元素」当前所在位置的前一位元素比他小,就停止。接着给下一个「待插入元素」找位置。
总共循环插入 length-1 次,∵ 开始时有序表中就已经包含 1 个元素了,∴ 是把后边 length-1 个元素往里插。
4. 代码实现
public class InsertSortDemo {
public static void main(String[] args) {
int[] array = {101, 34, 119, 1};
insertSortA(array);
}
// PlanA-移位
public static void insertSortA(int[] array) {
int insertVal, insertIndex;
for (int i = 1; i < array.length; i++) {
insertIndex = i;
insertVal = array[insertIndex];
while (insertIndex > 0 && insertVal < array[insertIndex - 1]) {
array[insertIndex] = array[insertIndex - 1];
insertIndex--;
}
if (insertIndex != i) array[insertIndex] = insertVal;
System.out.printf("Round %d: %s
", i, Arrays.toString(array));
}
}
// PlanB-交换
public static void insertSortB(int[] arr) {
int temp;
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0 && arr[j] < arr[j-1]; j--) {
temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
}