神经元:函数
神经网络(模型)的本质:函数网络
深度学习的本质:反向传播求偏导
梯度:向量(有大小和方向),函数在该点的方向导数取得最大值的方向,在该点处梯度的方向为函数变化最快的方向
梯度下降:梯度的负方向是函数下降最快的方向
收敛:取得最小值
权重:输入进入神经元前乘的数
偏置:乘完权重加的数
激活函数:将线性输入转化为非线性输出
全连接层:该层的每个神经元与前一层的所有神经元进行全连接
学习率:损失函数下降到最小值的速率,大了容易错过最佳方案甚至不收敛,小了会使网络训练的时间过长
batch与epoch
批量归一化:把输入值拉回到正态分布
原因:1、输入的数据与输出的数据的分布不一致,导致模型训练困难(因为模型学的是数据的分布)
2、使输出逐渐靠近激活函数梯度较小的地方,造成梯度消失。
卷积神经网络:广泛应用于图像数据,目的是为了减少参数数量,有多少个卷积核卷积之后就有多少层
滤波器:在CNN中与输入图像相乘的部分
池化:对矩阵进行压缩,减少一些参数,防止过拟合(参数多了就容易过拟合),max操作将原来的4*4的矩阵转化成2*2
数据增强:提高数据的质量,如旋转增亮
feather map 每一个通道就是一个feather map
预测的值是连续的是回归问题,预测的值是离散的是分类问题
线性回归:基于x预测y并且x与y符合线性关系
卷积:用于特征提取,全连接:用于分类
正则化:以增大训练误差为代价来减少测试误差,换句话说就是防止过拟合
L2正则化:在损失函数后加一个L2范数,所以说正则化是以增大误差为代价
L2范数:其实就是欧氏距离,别名:权重衰减
L1范数:各元素绝对值之和,可进行特征选择,即让特征系数为0
信息熵:衡量系统的不确定性。它的大小为消除系统不确定性所付出最小努力
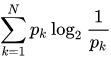
交叉熵:衡量在给定真实分布的情况下,用非真实分布所指定的策略消除系统中的不确定性所付出的努力
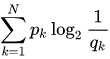
表示真实分布,
表示非真实分布