1. math数学函数
1.1 特殊常量
很多数学运算依赖于一些特殊的常量。math包含有π(pi)、e、nan(不是一个数)和infinity(无穷大)的值。
import math print(' π: {:.30f}'.format(math.pi)) print(' e: {:.30f}'.format(math.e)) print('nan: {:.30f}'.format(math.nan)) print('inf: {:.30f}'.format(math.inf))
π和e的精度仅受平台的浮点数C库限制。

1.2 测试异常值
浮点数计算可能导致两种类型的异常值。第一种是inf(无穷大),当用double存储一个浮点数,而该值会从一个具体很大绝对值的值上溢出时,就会出现这个异常值。
import math print('{:^3} {:6} {:6} {:6}'.format( 'e', 'x', 'x**2', 'isinf')) print('{:-^3} {:-^6} {:-^6} {:-^6}'.format( '', '', '', '')) for e in range(0, 201, 20): x = 10.0 ** e y = x * x print('{:3d} {:<6g} {:<6g} {!s:6}'.format( e, x, y, math.isinf(y), ))
当这个例子中的指数变得足够大时,x的平方无法再存放一个double中,这个值就会被记录为无穷大。

不过,并不是所有浮点数溢出都会导致inf值。具体地,用浮点值计算一个指数时,会产生OverflowError而不是保留inf结果。
x = 10.0 ** 200 print('x =', x) print('x*x =', x * x) print('x**2 =', end=' ') try: print(x ** 2) except OverflowError as err: print(err)
这种差异是由C和Python所用库中的实现差异造成的。

使用无穷大值的除法运算未定义。将一个数除以无穷大值的结果是nan(不是一个数)。
import math x = (10.0 ** 200) * (10.0 ** 200) y = x / x print('x =', x) print('isnan(x) =', math.isnan(x)) print('y = x / x =', x / x) print('y == nan =', y == float('nan')) print('isnan(y) =', math.isnan(y))
nan不等于任何值,甚至不等于其自身,所以要想检查nan,需要使用isnan()。

可以使用isfinite()检查其是普通的数还是特殊值inf或nan。
import math for f in [0.0, 1.0, math.pi, math.e, math.inf, math.nan]: print('{:5.2f} {!s}'.format(f, math.isfinite(f)))
如果是特殊值inf或nan,则isfinite()返回false,否则返回true。

1.3 比较
涉及浮点值的比较容易出错,每一步计算都可能由于数值表示而引入误差,isclose()函数使用一种稳定的算法来尽可能减少这些误差,同时完成相对和绝对比较。所用的公式等价于:
abs(a-b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)
默认地,isclose()会完成相对比较,容差被设置为le-09,这表示两个值之差必须小于或等于le乘以a和b中较大的绝对值。向isclose()传入关键字参数rel_tol可以改变这个容差。在这个例子中,值之间的差距必须在10%以内。
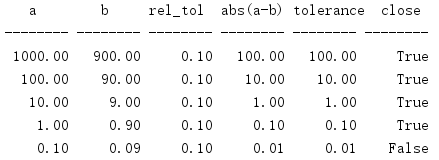
import math INPUTS = [ (1000, 900, 0.1), (100, 90, 0.1), (10, 9, 0.1), (1, 0.9, 0.1), (0.1, 0.09, 0.1), ] print('{:^8} {:^8} {:^8} {:^8} {:^8} {:^8}'.format( 'a', 'b', 'rel_tol', 'abs(a-b)', 'tolerance', 'close') ) print('{:-^8} {:-^8} {:-^8} {:-^8} {:-^8} {:-^8}'.format( '-', '-', '-', '-', '-', '-'), ) fmt = '{:8.2f} {:8.2f} {:8.2f} {:8.2f} {:8.2f} {!s:>8}' for a, b, rel_tol in INPUTS: close = math.isclose(a, b, rel_tol=rel_tol) tolerance = rel_tol * max(abs(a), abs(b)) abs_diff = abs(a - b) print(fmt.format(a, b, rel_tol, abs_diff, tolerance, close))
0.1和0.09之间的比较失败,因为误差表示0.1。
要使用一个固定或“绝对”容差,可以传入abs_tol而不是rel_tol。
import math INPUTS = [ (1.0, 1.0 + 1e-07, 1e-08), (1.0, 1.0 + 1e-08, 1e-08), (1.0, 1.0 + 1e-09, 1e-08), ] print('{:^8} {:^11} {:^8} {:^10} {:^8}'.format( 'a', 'b', 'abs_tol', 'abs(a-b)', 'close') ) print('{:-^8} {:-^11} {:-^8} {:-^10} {:-^8}'.format( '-', '-', '-', '-', '-'), ) for a, b, abs_tol in INPUTS: close = math.isclose(a, b, abs_tol=abs_tol) abs_diff = abs(a - b) print('{:8.2f} {:11} {:8} {:0.9f} {!s:>8}'.format( a, b, abs_tol, abs_diff, close))
对于绝对容差,输入值之差必须小于给定的容差。

nan和inf是特殊情况。
import math print('nan, nan:', math.isclose(math.nan, math.nan)) print('nan, 1.0:', math.isclose(math.nan, 1.0)) print('inf, inf:', math.isclose(math.inf, math.inf)) print('inf, 1.0:', math.isclose(math.inf, 1.0))
nan不接近任何值,包括它自身。inf只接近它自身。

1.4 将浮点值转换为整数
math模块中有3个函数用于将浮点值转换为整数。这3个函数分别采用不同的方法,并适用于不同的场合。
最简单的是trunc(),其会截断小数点后的数字,只留下构成这个值整数部分的有效数字。floor()将其输入转换为不大于它的最大整数,ceil()(上限)会生成按顺序排在这个输入值之后的最小整数。
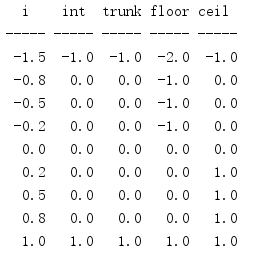
import math HEADINGS = ('i', 'int', 'trunk', 'floor', 'ceil') print('{:^5} {:^5} {:^5} {:^5} {:^5}'.format(*HEADINGS)) print('{:-^5} {:-^5} {:-^5} {:-^5} {:-^5}'.format( '', '', '', '', '', )) fmt = '{:5.1f} {:5.1f} {:5.1f} {:5.1f} {:5.1f}' TEST_VALUES = [ -1.5, -0.8, -0.5, -0.2, 0, 0.2, 0.5, 0.8, 1, ] for i in TEST_VALUES: print(fmt.format( i, int(i), math.trunc(i), math.floor(i), math.ceil(i), ))
trunc()等价于直接转换为int。
1.5 浮点值的其他表示
modf()取一个浮点数,并返回一个元组,其中包含这个输入值的小数和整数部分。
import math for i in range(6): print('{}/2 = {}'.format(i, math.modf(i / 2.0)))
返回值中的两个数字均为浮点数。
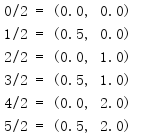
frexp()返回一个浮点数的尾数和指数,可以用这个函数创建值的一种更可移植的表示。
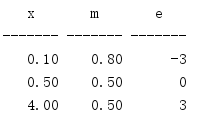
import math print('{:^7} {:^7} {:^7}'.format('x', 'm', 'e')) print('{:-^7} {:-^7} {:-^7}'.format('', '', '')) for x in [0.1, 0.5, 4.0]: m, e = math.frexp(x) print('{:7.2f} {:7.2f} {:7d}'.format(x, m, e))
frexp()使用公式x = m * 2**e,并返回值m和e。
ldexp()与frexp()正好相反。
import math print('{:^7} {:^7} {:^7}'.format('m', 'e', 'x')) print('{:-^7} {:-^7} {:-^7}'.format('', '', '')) INPUTS = [ (0.8, -3), (0.5, 0), (0.5, 3), ] for m, e in INPUTS: x = math.ldexp(m, e) print('{:7.2f} {:7d} {:7.2f}'.format(m, e, x))
ldexp()使用与frexp()相同的公式,取尾数和指数值作为参数,并返回一个浮点数。

1.6 正号和负号
一个数的绝对值就是不带正负号的本值。使用fabs()可以计算一个浮点数的绝对值。
import math print(math.fabs(-1.1)) print(math.fabs(-0.0)) print(math.fabs(0.0)) print(math.fabs(1.1))
在实际中,float的绝对值表示为一个正值。

要确定一个值的符号,以便为一组值指定相同的符号或者比较两个值,可以使用copysign()来设置正确值的符号。
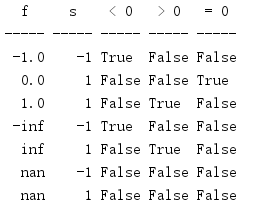
import math HEADINGS = ('f', 's', '< 0', '> 0', '= 0') print('{:^5} {:^5} {:^5} {:^5} {:^5}'.format(*HEADINGS)) print('{:-^5} {:-^5} {:-^5} {:-^5} {:-^5}'.format( '', '', '', '', '', )) VALUES = [ -1.0, 0.0, 1.0, float('-inf'), float('inf'), float('-nan'), float('nan'), ] for f in VALUES: s = int(math.copysign(1, f)) print('{:5.1f} {:5d} {!s:5} {!s:5} {!s:5}'.format( f, s, f < 0, f > 0, f == 0, ))
还需要另一个类似copysign()的函数,因为不能将nan和-nan与其他值直接比较。
1.7 常用计算
在二进制浮点数内存中表示精确度很有难度。有些值无法准确地表示,而且如果通过反复计算来处理一个值,那么计算越频繁就越容易引人表示误差。math包含一个函数来计算一系列浮点数的和,它使用一种高效的算法来尽量减少这种误差。
import math values = [0.1] * 10 print('Input values:', values) print('sum() : {:.20f}'.format(sum(values))) s = 0.0 for i in values: s += i print('for-loop : {:.20f}'.format(s)) print('math.fsum() : {:.20f}'.format(math.fsum(values)))
给定一个包含10个值的序列,每个值都等于0.1,这个序列总和的期望值为1.0。不过,由于0.1不能精确地表示为一个浮点数,所以会在总和中引入误差,除非用fsum()来计算。

factorial()常用于计算一系列对象的排列和组合数。一个正整数n的阶乘(表示为n!)被递归的定义为(n-1)!*n,并在0!==1停止递归。
import math for i in [0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.1]: try: print('{:2.0f} {:6.0f}'.format(i, math.factorial(i))) except ValueError as err: print('Error computing factorial({}): {}'.format(i, err))
factorial()只能处理整数,不过它确实也接受float参数,只要这个参数可以转换为一个整数而不丢值。

gamma()类似于factorial(),不过它可以处理实数,而且值会下移一个数(gamma等于(n - 1)!)。
import math for i in [0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6]: try: print('{:2.1f} {:6.2f}'.format(i, math.gamma(i))) except ValueError as err: print('Error computing gamma({}): {}'.format(i, err))
由于0会导致开始值为负,所以这是不允许的。

lgamma()会返回对输入值求gamma所得结果的绝对值的自然对数。
import math for i in [0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6]: try: print('{:2.1f} {:.20f} {:.20f}'.format( i, math.lgamma(i), math.log(math.gamma(i)), )) except ValueError as err: print('Error computing lgamma({}): {}'.format(i, err))
使用lgamma()会比使用gamma()结果单独计算对数更精确。

求模操作符(%)会计算一个除法表达式的余数(例如,5 % 2 = 1)。Python语言内置的这个操作符可以很好地处理整数,但是与很多其他浮点数运算类似,中间计算可能带来表示问题,从而进一步造成数据丢失。fmod()可以为浮点值提供一个更精确的实现。
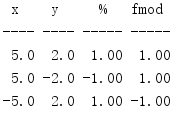
import math print('{:^4} {:^4} {:^5} {:^5}'.format( 'x', 'y', '%', 'fmod')) print('{:-^4} {:-^4} {:-^5} {:-^5}'.format( '-', '-', '-', '-')) INPUTS = [ (5, 2), (5, -2), (-5, 2), ] for x, y in INPUTS: print('{:4.1f} {:4.1f} {:5.2f} {:5.2f}'.format( x, y, x % y, math.fmod(x, y), ))
还有一点可能经常产生混淆,即fmod()计算模所使用的算法与%使用的算法也有所不同,所以结果的符号不同。
可以使用gcd()找出两个整数公约数中最大的整数——也就是最大公约数。
import math print(math.gcd(10, 8)) print(math.gcd(10, 0)) print(math.gcd(50, 225)) print(math.gcd(11, 9)) print(math.gcd(0, 0))
如果两个值都为0,则结果为0。

1.8 指数和对数
指数生长曲线在经济学、物理学和其他科学中经常出现。Python有一个内置的幂运算符(“**”),不过,如果需要将一个可调用函数作为另一个函数的参数,那么可能需要用到pow()。
import math INPUTS = [ # Typical uses (2, 3), (2.1, 3.2), # Always 1 (1.0, 5), (2.0, 0), # Not-a-number (2, float('nan')), # Roots (9.0, 0.5), (27.0, 1.0 / 3), ] for x, y in INPUTS: print('{:5.1f} ** {:5.3f} = {:6.3f}'.format( x, y, math.pow(x, y)))
1的任何次幂总返回1.0,同样,任何值的指数为0.0时也总是返回1.0.对于nan值(不是一个数),大多数运算都返回nan。如果指数小于1,pow()会计算一个根。

由于平方根(指数为1/2)被使用的非常频繁,所以有一个单独的函数来计算平方根。
import math print(math.sqrt(9.0)) print(math.sqrt(3)) try: print(math.sqrt(-1)) except ValueError as err: print('Cannot compute sqrt(-1):', err)
计算负数的平方根需要用到复数,这不在math的处理范围内。试图计算一个负值的平方根时,会导致一个ValueError。

对数函数查找满足条件x=b**y的y。默认log()计算自然对数(底数为e)。如果提供了第二个参数,则使用这个参数值作为底数。
import math print(math.log(8)) print(math.log(8, 2)) print(math.log(0.5, 2))
x小于1时,求对数会产生负数结果。

log()有三个变形。在给定浮点数表示和取整误差的情况下,由log(x,b)生成的计算值只有有限的精度(特别是对于某些底数)。log10()完成log(x,10)计算,但是会使用一种比log()更精确的算法。
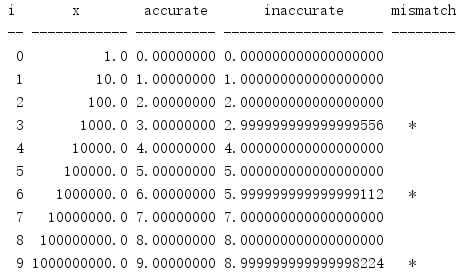
import math print('{:2} {:^12} {:^10} {:^20} {:8}'.format( 'i', 'x', 'accurate', 'inaccurate', 'mismatch', )) print('{:-^2} {:-^12} {:-^10} {:-^20} {:-^8}'.format( '', '', '', '', '', )) for i in range(0, 10): x = math.pow(10, i) accurate = math.log10(x) inaccurate = math.log(x, 10) match = '' if int(inaccurate) == i else '*' print('{:2d} {:12.1f} {:10.8f} {:20.18f} {:^5}'.format( i, x, accurate, inaccurate, match, ))
输出中末尾有*的行突出强调了不精确的值。
类似于log10(),log2()会完成等价于math.log(x,2)的计算。
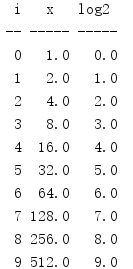
import math print('{:>2} {:^5} {:^5}'.format( 'i', 'x', 'log2', )) print('{:-^2} {:-^5} {:-^5}'.format( '', '', '', )) for i in range(0, 10): x = math.pow(2, i) result = math.log2(x) print('{:2d} {:5.1f} {:5.1f}'.format( i, x, result, ))
取决于底层平台,这个内置的特殊用途函数能提供更好的性能和精度,因为它利用了针对底数2的特殊用途算法,而在更一般用途的函数中没有使用这些算法。
log1p()会计算Newton-Mercator序列(1+x的自然对数)。
import math x = 0.0000000000000000000000001 print('x :', x) print('1 + x :', 1 + x) print('log(1+x):', math.log(1 + x)) print('log1p(x):', math.log1p(x))
对于非常接近于0的x,log1p()会更为精确,因为它使用的算法可以补偿由初识加法带来的取整误差。

exp()会计算指数函数(e**x)。
import math x = 2 fmt = '{:.20f}' print(fmt.format(math.e ** 2)) print(fmt.format(math.pow(math.e, 2))) print(fmt.format(math.exp(2)))
类似于其他特殊函数,与等价的通用函数math.pow(math.e,x)相比,exp()使用的算法可以生成更精确的结果。
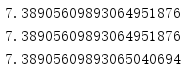
expm1()是log1p()的逆运算,会计算e**x-1。
import math x = 0.0000000000000000000000001 print(x) print(math.exp(x) - 1) print(math.expm1(x))
类似于log1p(),x值很小时,如果单独完成减法,则可能会损失精度。

1.9 角
尽管我们每天讨论角时更常用的是度,但弧度才是科学和数学领域中度量角度的标准单位。弧度是在圆心相交的两条线所构成的角,其终点落在圆的圆周上,终点之间相距一个弧度。
圆周长计算为2πr,所以弧度与π(这是三角函数计算中经常出现的一个值)之间存在一个关系。这个关系使得三角学和微积分中都使用了弧度,因为利用弧度可以得到更紧凑的公式。
要把度转换为弧度,可以使用redians()。
import math print('{:^7} {:^7} {:^7}'.format( 'Degrees', 'Radians', 'Expected')) print('{:-^7} {:-^7} {:-^7}'.format( '', '', '')) INPUTS = [ (0, 0), (30, math.pi / 6), (45, math.pi / 4), (60, math.pi / 3), (90, math.pi / 2), (180, math.pi), (270, 3 / 2.0 * math.pi), (360, 2 * math.pi), ] for deg, expected in INPUTS: print('{:7d} {:7.2f} {:7.2f}'.format( deg, math.radians(deg), expected, ))
转换公式为rad = deg * π / 180。

要从弧度转换为度,可以使用degrees()。
import math INPUTS = [ (0, 0), (math.pi / 6, 30), (math.pi / 4, 45), (math.pi / 3, 60), (math.pi / 2, 90), (math.pi, 180), (3 * math.pi / 2, 270), (2 * math.pi, 360), ] print('{:^8} {:^8} {:^8}'.format( 'Radians', 'Degrees', 'Expected')) print('{:-^8} {:-^8} {:-^8}'.format('', '', '')) for rad, expected in INPUTS: print('{:8.2f} {:8.2f} {:8.2f}'.format( rad, math.degrees(rad), expected, ))
具体转换公式为deg = rad * 180 / π。

1.10 三角函数
三角函数将三角形中的角与其边长相关联。在有周期性质的公式中经常出现三角函数,如谐波或圆周运动;在处理角时也会经常用到三角函数。标准库中所有三角函数的角参数都被表示为弧度。
给定一个直角三角形中的角,其正弦是对边长度与斜边长度之比(sin A = 对边/斜边)。余弦是邻边长度与斜边长度之比(cos A = 邻边/斜边)。正切是对边与邻边之比(tan A = 对边/邻边)。
import math print('{:^7} {:^7} {:^7} {:^7} {:^7}'.format( 'Degrees', 'Radians', 'Sine', 'Cosine', 'Tangent')) print('{:-^7} {:-^7} {:-^7} {:-^7} {:-^7}'.format( '-', '-', '-', '-', '-')) fmt = '{:7.2f} {:7.2f} {:7.2f} {:7.2f} {:7.2f}' for deg in range(0, 361, 30): rad = math.radians(deg) if deg in (90, 270): t = float('inf') else: t = math.tan(rad) print(fmt.format(deg, rad, math.sin(rad), math.cos(rad), t))
正切也可以被定义为角的正弦值与其余弦值之比,因为弧度π/2和3π/2的余弦是0,所以相应的正切值为无穷大。

给定一个点(x,y),点[(0,0),(x,0),(x,y)]构成的三角形中斜边长度为(x**2+y**2)**1/2,可以用hypot()来计算。
import math print('{:^7} {:^7} {:^10}'.format('X', 'Y', 'Hypotenuse')) print('{:-^7} {:-^7} {:-^10}'.format('', '', '')) POINTS = [ # simple points (1, 1), (-1, -1), (math.sqrt(2), math.sqrt(2)), (3, 4), # 3-4-5 triangle # on the circle (math.sqrt(2) / 2, math.sqrt(2) / 2), # pi/4 rads (0.5, math.sqrt(3) / 2), # pi/3 rads ] for x, y in POINTS: h = math.hypot(x, y) print('{:7.2f} {:7.2f} {:7.2f}'.format(x, y, h))
对于圆上的点,其斜边总是等于1。

还可以用这个函数查看两个点之间的距离。
import math print('{:^8} {:^8} {:^8} {:^8} {:^8}'.format( 'X1', 'Y1', 'X2', 'Y2', 'Distance', )) print('{:-^8} {:-^8} {:-^8} {:-^8} {:-^8}'.format( '', '', '', '', '', )) POINTS = [ ((5, 5), (6, 6)), ((-6, -6), (-5, -5)), ((0, 0), (3, 4)), # 3-4-5 triangle ((-1, -1), (2, 3)), # 3-4-5 triangle ] for (x1, y1), (x2, y2) in POINTS: x = x1 - x2 y = y1 - y2 h = math.hypot(x, y) print('{:8.2f} {:8.2f} {:8.2f} {:8.2f} {:8.2f}'.format( x1, y1, x2, y2, h, ))
使用x值之差和y值之差将一个端点移至原点,然后将结果传入hypot()。
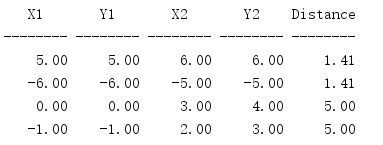
math还定义了反三角函数。
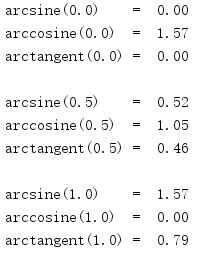
import math for r in [0, 0.5, 1]: print('arcsine({:.1f}) = {:5.2f}'.format(r, math.asin(r))) print('arccosine({:.1f}) = {:5.2f}'.format(r, math.acos(r))) print('arctangent({:.1f}) = {:5.2f}'.format(r, math.atan(r))) print()
1.57大约对于π/2,或90度,这个角的正弦为1,余弦为0。
1.11 双曲函数
双曲函数经常出现在线性微分方程中,处理电磁场、流体力学、狭义相对论和其他高级物理和数学问题时常会用到。
import math print('{:^6} {:^6} {:^6} {:^6}'.format( 'X', 'sinh', 'cosh', 'tanh', )) print('{:-^6} {:-^6} {:-^6} {:-^6}'.format('', '', '', '')) fmt = '{:6.4f} {:6.4f} {:6.4f} {:6.4f}' for i in range(0, 11, 2): x = i / 10.0 print(fmt.format( x, math.sinh(x), math.cosh(x), math.tanh(x), ))
余弦函数和正弦函数构成一个圆,而双曲余弦函数和双曲正弦函数构成半个双曲线。
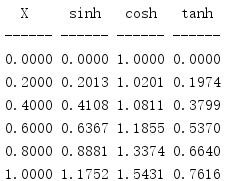
另外还提供了反双曲函数acosh()、asinh()和atanh()。
1.12 特殊函数
统计学中经常用到高斯误差函数(Gauss error function)。
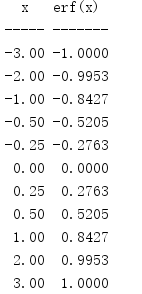
import math print('{:^5} {:7}'.format('x', 'erf(x)')) print('{:-^5} {:-^7}'.format('', '')) for x in [-3, -2, -1, -0.5, -0.25, 0, 0.25, 0.5, 1, 2, 3]: print('{:5.2f} {:7.4f}'.format(x, math.erf(x)))
对于误差函数,erf(-x) == -erf(x)。
补余误差函数erfc()生成等价于1 - erf(x)的值。
import math print('{:^5} {:7}'.format('x', 'erfc(x)')) print('{:-^5} {:-^7}'.format('', '')) for x in [-3, -2, -1, -0.5, -0.25, 0, 0.25, 0.5, 1, 2, 3]: print('{:5.2f} {:7.4f}'.format(x, math.erfc(x)))
如果x值很小,那么在从1做减法时erfc()实现便可以避免可能的精度误差。
