树的深度优先搜索(上):如何才能高效率地查字典?
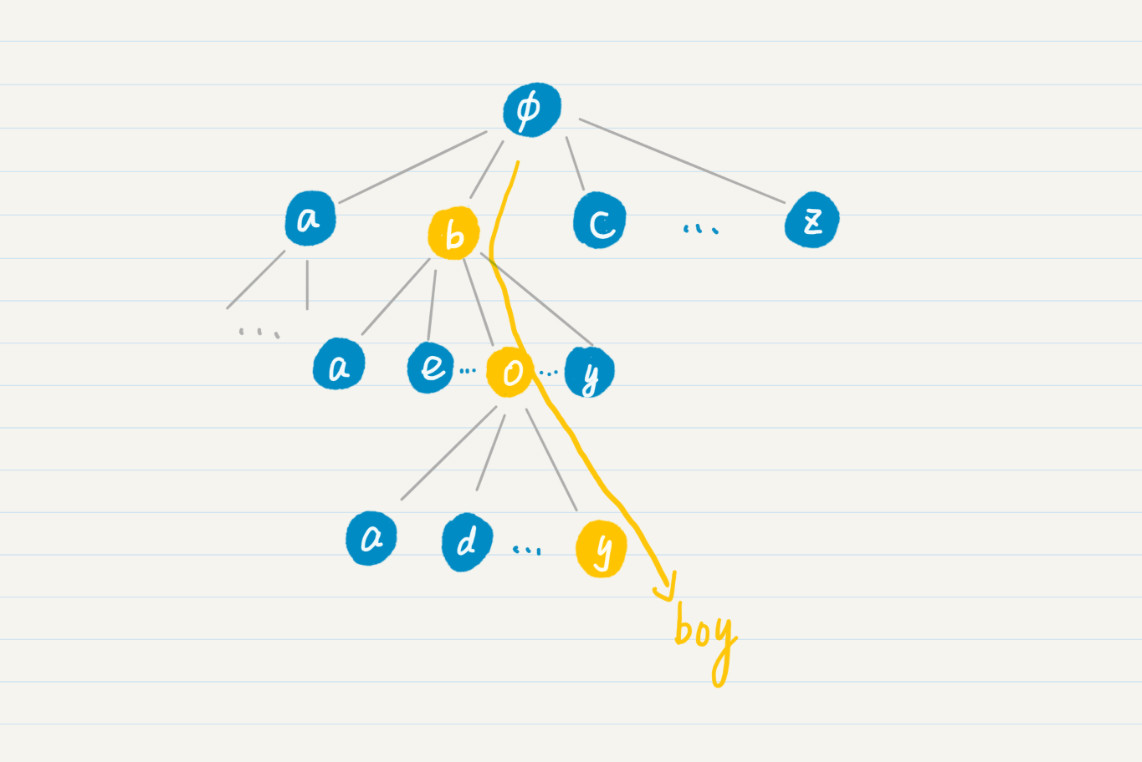
在平时的生活中,我们查字典都是从单词的最左边的字母开始,逐个去查找。比如查找“boy”这个单词,我们一般是这么查的。首先,在 a~z 这 26 个英文字母里找到单词的第一个字母 b,然后在 b 开头的单词里找到字母 o,最终在 bo 开头的单词里找到字母 y。
图论的一些基本概念
前缀树是一种有向树。那什么是有向树?顾名思义,有向树就是一种树,特殊的就是,它的边是有方向的。而树是没有简单回路的连通图。
如果一个图里所有的边都是有向边,那么这个图就是有向图。如果一个图里所有的边都是无向边,那么这个图就是无向图。既含有向边,又含无向边的图,称为混合图。
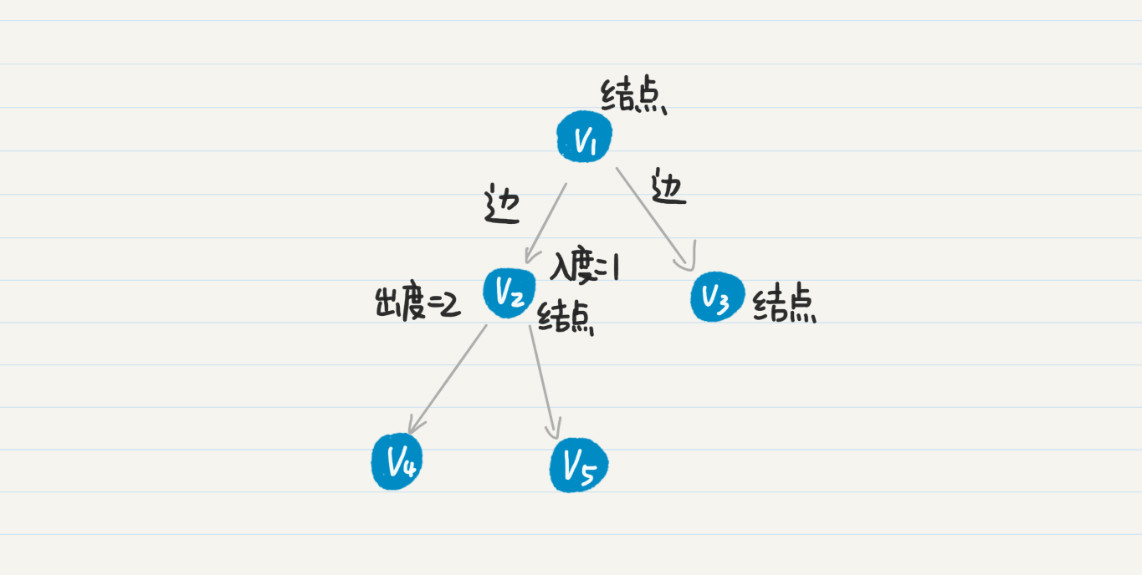
在有向图中,以结点 v 为出发点的边的数量,我们叫作 v 的出度。而以 v 为 终点的边之数量,称为 v 的入度。在上图中,结点 v2 的入度是 1,出度是 2。
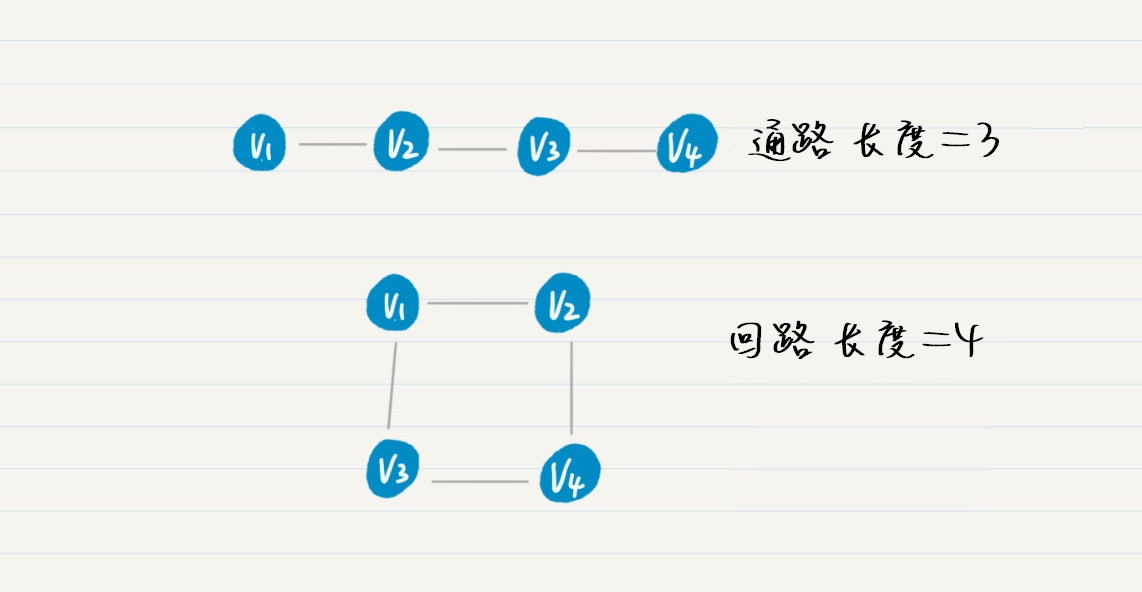
结点和边的交替序列组成的就是通路。所以,通路上的任意两个结点其实就是互为连通的。如果一条通路的起始点 v_{1} 和终止点 v_{n} 相同,这种特殊的通路我们就叫作回路。从起始点到终止点所经过的边之数量,就是通路的长度。这里我画了一张图,这里面有 1 条通路和 1 条回路,第一条非回路通路的长度是 3,第二条回路的长度是 4。
树是一种特殊的图,它是没有简单回路的连通无向图。这里的简单回路,其实就是指,除了第一个结点和最后一个结点相同外,其余结点不重复出现的回路。
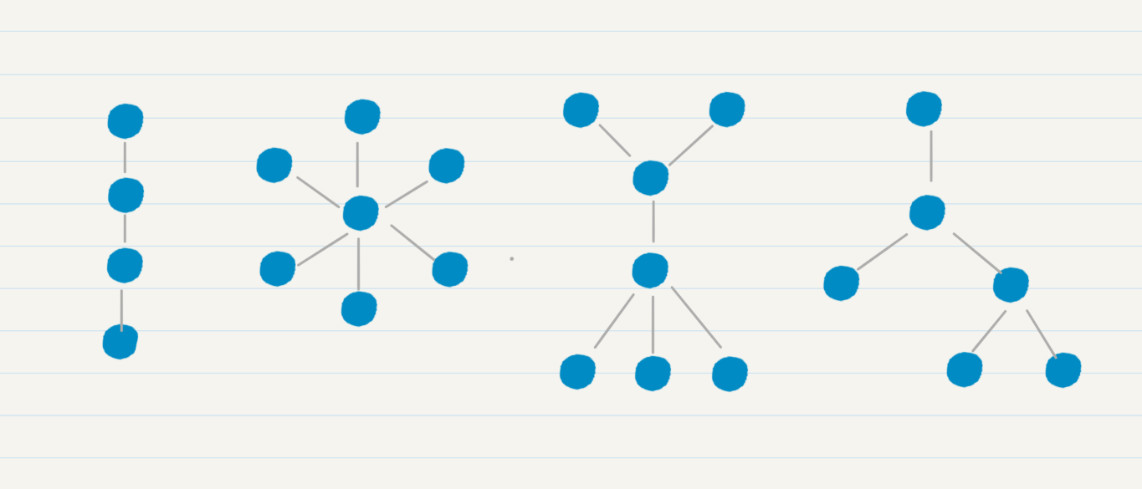
什么是有向树呢?顾名思义,有向树是一种特殊的树,其中的边都是有向的,而且它满足以下几个条件:
- 有且仅有一个结点的入度为 0,这个结点被称为根;
- 除根以外的所有结点,入度都为 1。从树根到任一结点有且仅有一条有向通路。
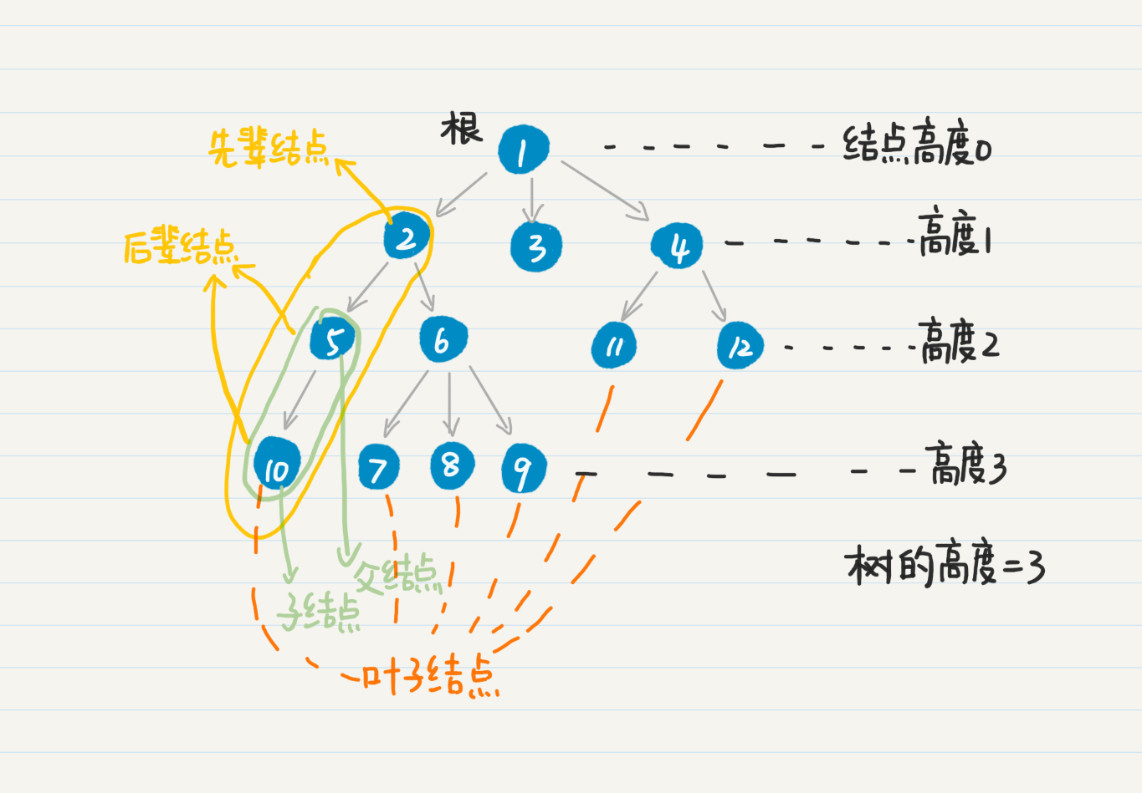
除了这些基本定义,有向树还有几个重要的概念,父结点、子结点、兄弟结点、先辈结点、后辈结点、叶子结点、结点的高度(或深度)、树的高度(或深度)。
前缀树的构建和查询
如何使用有向树来实现前缀树:构建前缀树和查询前缀树。
-
构建前缀树
-
查询前缀树
从前缀树的根开始,查找下一个结点,顺着这个通路走下去,一直走到到某个结点。如果这个结点及其前缀代表了一个存在的单词,而待查找的单词和这个结点及其前缀正好完全匹配,那就说明成功找到了一个单词。否则,就表示无法找到。
这里有几种特殊情况,需要注意。
- 如果还没到叶子结点的时候,待查的单词就结束了。这个时候要看最后匹配上的非叶子结点是否代表一个单词;如果不是,那说明被查单词并不在字典中。
- 如果搜索到前缀树的叶子结点,但是被查单词仍有未处理的字母。由于叶子结点没有子结点,这时候,被查单词不可能在字典中。
- 如果搜索到一半,还没到达叶子结点,被查单词也有尚未处理的字母,但是当前被处理的字母已经无法和结点上的字符匹配了。这时候,被查单词不可能在字典中。
构建的时候,我们需要根据当前的前缀进行查询,然后才能找到合适的位置插入新的结点。而且,这两者都存在一个不断重复迭代的查找过程,我们把这种方式称为深度优先搜索(Depth First Search)。
所谓树的深度优先搜索,其实就是从树中的某个结点出发,沿着和这个结点相连的边向前走,找到下一个结点,然后以这种方式不断地发现新的结点和边,一直搜索下去,直到访问了所有和出发点连通的点、或者满足某个条件后停止。
如果到了某个点,发现和这个点直接相连的所有点都已经被访问过,那么就回退到在这个点的父结点,继续查看是否有新的点可以访问;如果没有就继续回退,一直到出发点。由于单棵树中所有的结点都是连通的,所以通过深度优先的策略可以遍历树中所有的结点,因此也被称为深度优先遍历。
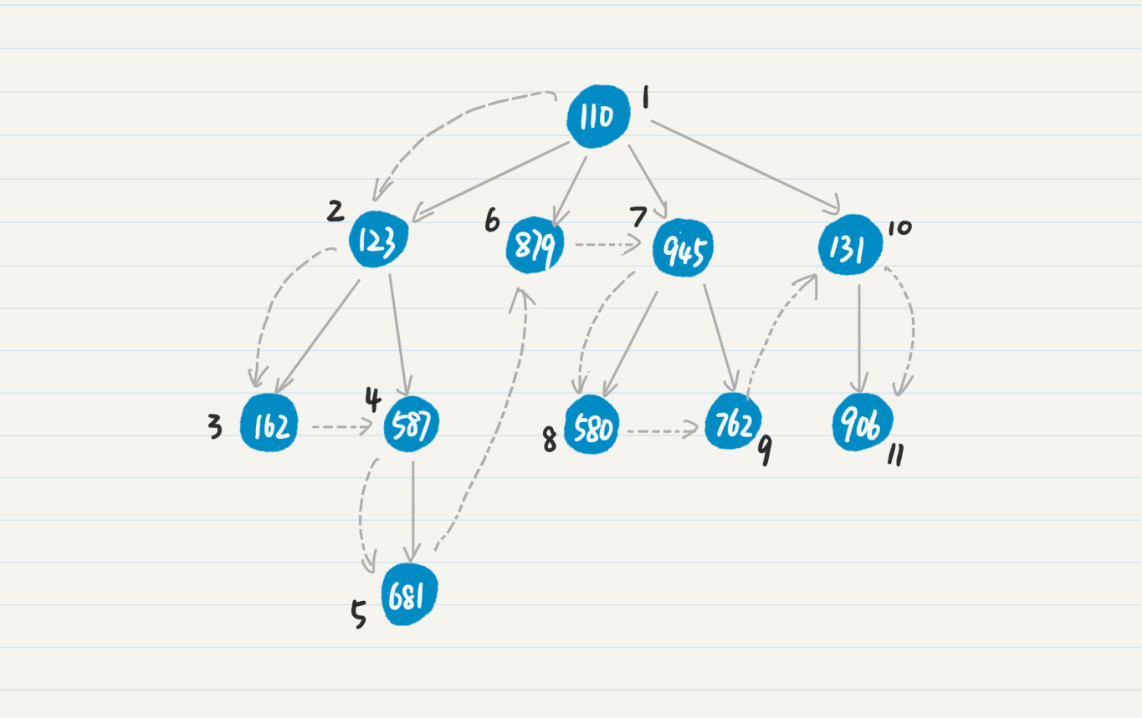
结点上的数字表示结点的 ID,而虚线表示遍历前进的方向,结点边上的数字表示该结点在深度优先搜索中被访问的顺序。在深度优先的策略下,我们从点 110 出发,然后发现和 110 相连的点 123,访问 123 后继续发现和 123 相连的点 162,再往后发现 162 没有出度,因此回退到 123,查看和 123 相连的另一个点 587,根据 587 的出度继续往前推进,如此类推。
总结
二叉树是每个结点最多有两个子树的树结构,它可用于二叉查找树和二叉堆。二叉树甚至可以用于图示化我们之前聊过的二分迭代。
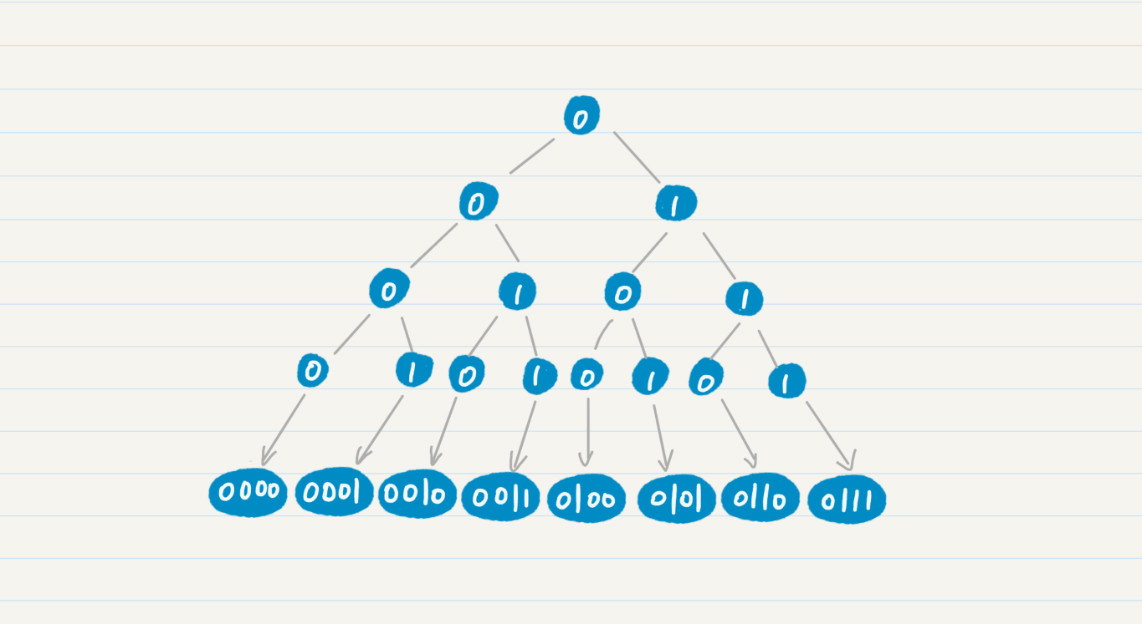
满二叉树是一棵高度为 n(高度从 1 开始计),且有 2^n-1 个结点的二叉树。在高度为 k(0<k≤n)的这一层上,结点的数量为 2^(k-1)。如果把树的根标为 0,每个结点的左子结点标为 0,每个结点的右子结点标为 1,那么把根到叶子结点的所有 0 或 1 连起来,就正好对应一个二进制数。