迭代法

迭代法：不用编程语言的自带函数，你会如何计算平方根？

什么是迭代法？

迭代法，简单来说，其实就是不断地用旧的变量值，递推计算新的变量值。

迭代法的思想，很容易通过计算机语言中的循环语言来实现。

迭代法有什么具体应用？

• 求数值的精确或者近似解。典型的方法包括二分法（Bisection method）和牛顿迭代法（Newton’s method）。
• 在一定范围内查找目标值。典型的方法包括二分查找。
• 机器学习算法中的迭代。相关的算法或者模型有很多，比如 K- 均值算法（K-means clustering）、PageRank 的马尔科夫链（Markov chain）、梯度下降法（Gradient descent）等等。迭代法之所以在机器学习中有广泛的应用，是因为很多时候机器学习的过程，就是根据已知的数据和一定的假设，求一个局部最优解。而迭代法可以帮助学习算法逐步搜索，直至发现这种解。

1. 求方程的精确或者近似解

计算某个给定正整数 n（n>1）的平方根

采用迭代中常见的二分法。每次查看区间内的中间值，检验它是否符合标准。

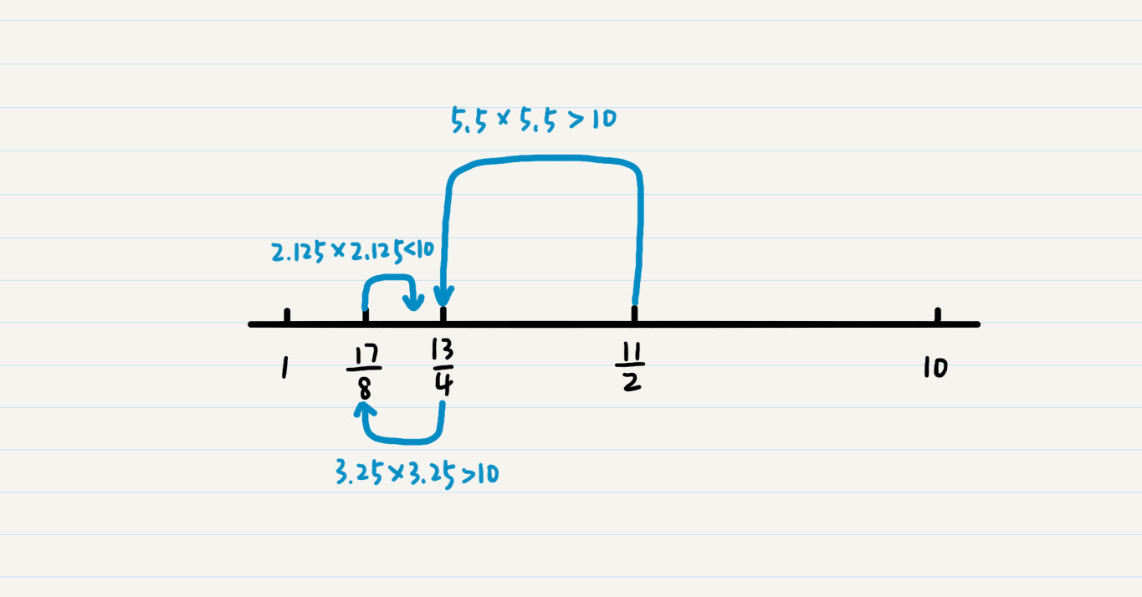
举个例子，假如我们要找到 10 的平方根。我们需要先看 1 到 10 的中间数值，也就是 11/2=5.5。5.5 的平方是大于 10 的，所以我们要一个更小的数值，就看 5.5 和 1 之间的 3.25。由于 3.25 的平方也是大于 10 的，继续查看 3.25 和 1 之间的数值，也就是 2.125。这时，2.125 的平方小于 10 了，所以看 2.125 和 3.25 之间的值，一直继续下去，直到发现某个数的平方正好是 10。

• 牛顿迭代法

用于求方程的近似解。这种方法以微分为基础，每次迭代的时候，它都会去找到比上一个值 x_{0} 更接近的方程的根，最终找到近似解。

2. 查找匹配记录

二分法中的迭代式逼近，不仅可以帮我们求得近似解，还可以帮助我们查找匹配的记录。

• 用二分查找法进行字典查询的思路

第一步，将整个字典先进行排序（假设从小到大）。二分法中很关键的前提条件是，所查找的区间是有序的。这样才能在每次折半的时候，确定被查找的对象属于左半边还是右半边。

第二步，使用二分法逐步定位到被查找的单词。每次迭代的时候，都找到被搜索区间的中间点，看看这个点上的单词，是否和待查单词一致。如果一致就返回；如果不一致，要看被查单词比中间点上的单词是小还是大。如果小，那说明被查的单词如果存在字典中，那一定在左半边；否则就在右半边。

第三步，根据第二步的判断，选择左半边或者后半边，继续迭代式地查找，直到范围缩小到单个的词。如果到最终仍然无法找到，则返回不存在。

第一，每次判断是否终结迭代的条件不同。求平方根的时候，我们需要判断某个数的平方是否和输入的数据一致。而这里，我们需要判断字典中某个单词是否和待查的单词相同。

第二，二分查找需要确保被搜索的空间是有序的。

总结