链表

一： 链表的引入

1 链表的功能

1 顺序表的构建需要预先知道数据大小来申请连续的存储空间，而在进行扩充时又需要进行数据的搬迁，所以使用起来并不是很灵活。
2 链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。

2 链表的概念

1 链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。
2 链表是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是在每一个结点（数据存储单元）里存放下一个结点的位置信息（即地址）。

二：单向链表

1 单向链表的概念

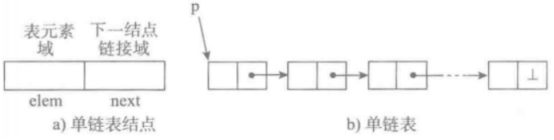
1 单向链表也叫单链表，是链表中最简单的一种形式。
2 它的每个结点包含两个域，一个信息域（元素域）和一个链接域。
3 这个链接指向链表中的下一个结点，而最后一个结点的链接域则指向一个空值。

2 单向链表的操作

1 is_empty() 链表是否为空
2 length() 链表长度
3 travel() 遍历整个链表
4 append(item) 链表尾部添加元素
5 add(item) 链表头部添加元素
6 insert(pos, item) 指定位置添加元素
7 search(item) 查找结点是否存在
8 remove(item) 删除结点

3 单个节点的实现

# 定义链表的单个结点
class Node():
    # 构造方法初始化结点
    def __init__(self, elem):
        # 初始化数据区
        self.elem = elem
        # 初始化链接区
        self.next = None

4 单链表的实现

 初始化

# 定义单链表
class single_linked_list():
    # 构造链表，若结点没值指向None
    def __init__(self,node=None):
        # __head代表头结点
        self.__head = node

 判断非空

# 判断链表是否为空
def is_empty(self):
    # head指向None则为空
    return self.__head is None

 cur游标代表当前结点

 

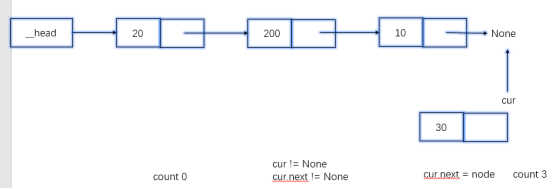
# 查长度
def length(self):
    # 判断空
    if self.is_empty():
        return 0
    else:
        # 定义游标
        cur = self.__head
        # 计数
        count = 0
        # 循环
        while cur != None:
            # 让游标移动
            cur = cur.next
            count += 1
        return count

l 遍历，注意进循环后先打印，再移动游标

def travel(self):
    if self.is_empty():
        return
    else:
        # 游标
        cur = self.__head
        while cur != None:
            # 先打印
            print(cur.elem,end= ' ')
            cur = cur.next
        print('')

尾插法

def append(self,item):
    # 定义新结点
    node = Node(item)
    if self.is_empty():
        self.__head = node
    else:
        cur = self.__head
        # cur到最后一个结点停下
        while cur.next != None:
            # cur移动
            cur = cur.next
        # 此时，cur到达了最后一个结点
        cur.next = node

头插法

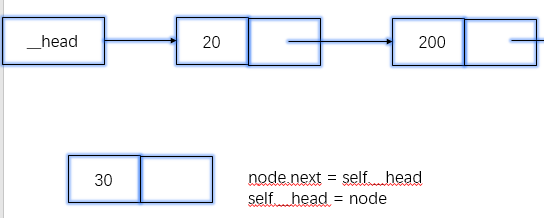
def add(self,item):
    # 新结点
    node = Node(item)
    if self.is_empty():
        self.__head = node
    else:
        # 这里顺序不能变
        node.next = self.__head
        self.__head = node

在指定位置添加

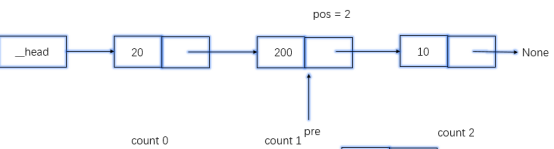
# pos从0开始
def insert(self,pos,item):
    # 特殊判断，友好一点
    if pos < 0:
        self.add(item)
    elif pos > (self.length()-1):
        self.append(item)
    else:
        # 新结点
        node = Node(item)
        pre = self.__head
        count = 0
        while count < (pos -1):
            # 移动游标
            pre = pre.next
            count += 1
        # 此时，pre游标指向插入位置的前一个结点
        # 下面操作顺序不能变
        node.next = pre.next
        pre.next = node

l 查找元素，循环遍历比对每一个元素

def search(self,item):
    if self.is_empty():
        return False
    else:
        # 定义游标
        cur = self.__head
        while cur != None:
            # 判断cur的数据是否为查找的数据item
            if cur.elem == item:
                return True
            else:
                # 游标移动
                cur = cur.next
        # 遍历完成，cur指向None
        return False

删除元素，需要两个游标

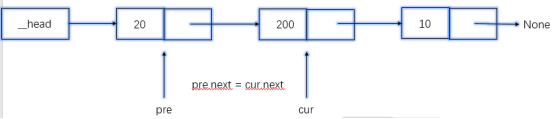
def remove(self,item):
    if self.is_empty():
        return
    else:
        # 定义cur游标
        cur = self.__head
        # 定义pre游标
        pre = None
        # 查找所有的位置有没有要删除的，若有则删
        while cur != None:
            # 判断cur指向的数据，是否为要删的数据
            if cur.elem == item:
                # 考虑特殊情况，恰好要删的是第一个元素
                if cur == self.__head:
                    # 头结点指向后一个结点
                    self.__head = cur.next
                else:
                    # 删除
                    pre.next = cur.next
                return
            else:
                # 移动游标，先移动pre，再移动cur
                pre = cur
                cur = cur.next

测试

if __name__ == '__main__':
    sll = single_linked_list()
    print(sll.is_empty())
    print(sll.length())
    print('--------------------------')
    sll.travel()
    print('--------------------------')
    sll.append(2)
    sll.add(3)
    sll.append(5)
    sll.travel()
    print('--------------------------')
    print(sll.is_empty())
    print(sll.length())
    print('--------------------------')
    sll.insert(1,'abc')
    sll.travel()
    print(sll.search(5))
    print('--------------------------')
    sll.remove('abc')
    sll.travel()

5 链表与顺序表的对比

1 链表失去了顺序表随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大，但对存储空间的使用要相对灵活。
2 请填写链表与顺序表各种操作的时间复杂度：

操作	链表	顺序表
访问元素	O(n)	O(1)
在头部插入/删除	O(1)	O(n)
在尾部插入/删除	O(n)	O(1)
在中间插入/删除	O(n)	O(n)

 三  双向链表

 1 双向链表的概念

1 一种更复杂的链表是“双向链表”或“双面链表”。
2 每个结点有两个链接：一个指向前一个结点，当此结点为第一个结点时，指向空值。
3 而另一个指向下一个结点，当此结点为最后一个结点时，指向空值。
4 前一个结点称为前趋结点，后一个结点称为后继结点

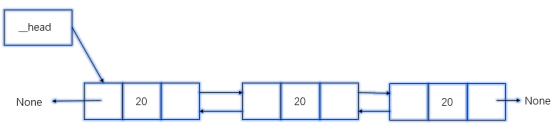
2 双向链表的操作

is_empty() 链表是否为空
length() 链表长度
travel() 遍历整个链表
append(item) 链表尾部添加元素
add(item) 链表头部添加元素
insert(pos, item) 指定位置添加元素
search(item) 查找结点是否存在
remove(item) 删除结点

3 单个节点的实现

# 定义双向链表的结点
class Node:
    def __init__(self,elem):
        # 初始化数据区
        self.elem = elem
        self.next = None
        self.prev = None

4 双向链表的实现

# 实现双链表
class double_linked_list:
    # 构造链表，若结点没值指向None
    def __init__(self,node=None):
        # __head代表头结点
        self.__head = node
    # 判断链表是否为空
    def is_empty(self):
        # head指向None则为空
        return self.__head is None
    # 查长度
    def length(self):
        # 判断空
        if self.is_empty():
            return 0
        else:
            # 定义游标
            cur = self.__head
            # 计数
            count = 0
            # 循环
            while cur != None:
                # 让游标移动
                cur = cur.next
                count += 1
            return count
    def travel(self):
        if self.is_empty():
            return
        else:
            # 游标
            cur = self.__head
            while cur != None:
                # 先打印
                print(cur.elem,end= ' ')
                cur = cur.next
            print('')

尾插要处理前驱

def append(self,item):
    node = Node(item)
    if self.is_empty():
        self.__head = node
    else:
        # 移动游标
        cur = self.__head
        while cur.next != None:
            cur = cur.next
        # 此时，cur指向最后一个结点
        cur.next = node
        # 处理前驱结点
        node.prev = cur

头插

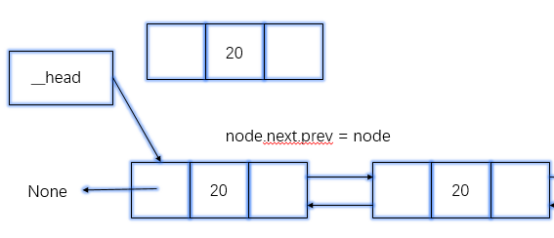
def add(self,item):
    node = Node(item)
    if self.is_empty():
        self.__head = node
    else:
        # 新结点指向原第一个结点
        node.next = self.__head
        self.__head = node
        # 处理原第一个结点的前驱
        node.next.prev = node

指定位置插入

def insert(self,pos,item):
    if pos < 0:
        self.add(item)
    elif pos > (self.length() -1):
        self.append(item)
    else:
        # 创建结点
        node = Node(item)
        # 游标
        cur = self.__head
        count = 0
        # 因为cur停在后一个位置，所以看图吧
        while count < pos:
            cur = cur.next
            count += 1
        # 此时，cur停在后一个结点
        node.next = cur
        node.prev = cur.prev
        cur.prev.next = node
        cur.prev = node

删除元素

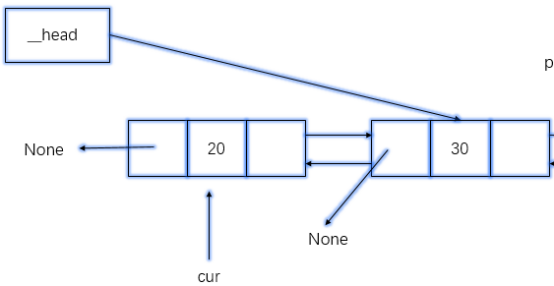
def remove(self,item):
    if self.is_empty():
        return
    else:
        cur = self.__head
        while cur != None:
            # 对比是否为要删的元素
            if cur.elem == item:
                # 考虑特殊情况，若找到的结点，恰好为第一个结点
                if cur == self.__head:
                    # 头直接指向后一个结点
                    self.__head = cur.next
                    # 考虑链表只有一个结点的情况下，None.prev会出问题
                    if cur.next:
                        cur.next.prev = None
                else:
                    # 当前结点的前一个指向后一个
                    cur.prev.next = cur.next
                    # 考虑后面没有结点的情况
                    if cur.next:
                        cur.next.prev = cur.prev
                return
            else:
                cur = cur.next

l 测试用前面的代码

if __name__ == '__main__':
    sll = single_linked_list()
    print(sll.is_empty())
    print(sll.length())
    print('--------------------------')
    sll.travel()
    print('--------------------------')
    sll.append(2)
    sll.add(3)
    sll.append(5)
    sll.travel()
    print('--------------------------')
    print(sll.is_empty())
    print(sll.length())
    print('--------------------------')
    sll.insert(1,'abc')
    sll.travel()
    print(sll.search(5))
    print('--------------------------')
    sll.remove('abc')
    sll.travel()

四 单向循环链表

1单向循环链表的概念

1 单链表的一个变形是单向循环链表。
2 链表中最后一个结点的next域不再为None，而是指向链表的头结点。

2 单向循环链表的操作

is_empty() 链表是否为空
length() 链表长度
travel() 遍历整个链表
append(item) 链表尾部添加元素
add(item) 链表头部添加元素
insert(pos, item) 指定位置添加元素
search(item) 查找结点是否存在
remove(item) 删除结点

3单个节点的实现（与单向链表一样）

4 单向循环链表的实现

定义单向循环链表

# 定义单向循环链表
class single_loop_list:
    def __init__(self,node=None):
        self.__head = node
        # 特殊处理回环
        if node:
            node.next = node

求长度

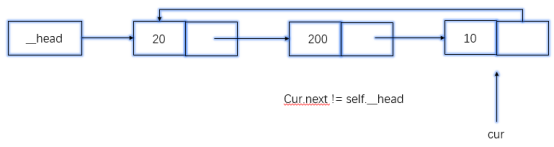
def length(self):
    if self.is_empty():
        return 0
    else:
        cur = self.__head
        # count从1开始
        count = 1
        while cur.next != self.__head:
            # 移动
            cur = cur.next
            count += 1
        return count

遍历，注意不要把最后一个漏掉了

def travel(self):
    if self.is_empty():
        return
    else:
        cur = self.__head
        while cur.next != self.__head:
            # 先打印再移动游标
            print(cur.elem,end=' ')
            cur = cur.next
        # 退出循环，cur指向了尾结点
        print(cur.elem,end=' ')
        print('')

尾插法，处理回环

def append(self,item):
    node = Node(item)
    if self.is_empty():
        self.__head = node
        # 处理回环
        node.next = node
    else:
        # 游标走到最后
        cur = self.__head
        while cur.next != self.__head:
            cur = cur.next
        # cur此时在最后一个位置
        # 新结点指向头
        node.next = self.__head
        # 原最后结点，指向新结点
        cur.next = node

头插，要处理回环

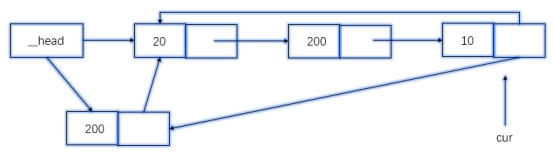
def add(self,item):
    # 结点
    node = Node(item)
    if self.is_empty():
        self.__head = node
        node.next = node
    else:
        cur =self.__head
        # 移动游标
        while cur.next != self.__head:
            cur = cur.next
        # cur停留在最后的位置
        node.next = self.__head
        self.__head = node
        # 形成回环
        cur.next = node

 指定位置插入，与单向链表一样

查找元素，注意别丢下最后一个

def search(self,item):
    if self.is_empty():
        return False
    else:
        # 定义游标
        cur = self.__head
        while cur.next != self.__head:
            # 判断cur的数据是否为查找的数据item
            if cur.elem == item:
                return True
            else:
                # 游标移动
                cur = cur.next
        # 处理最后一个结点
        if cur.elem == item:
            return True
        # 遍历完成，cur指向None
        return False

删除元素

def remove(self, item):
    if self.is_empty():
        return
    else:
        cur = self.__head
        pre = None
        # 循环条件
        while cur.next != self.__head:
            # 判断cur的数据是否为要删的数据
            if cur.elem == item:
                if cur == self.__head:
                    # 考虑删的恰好是第一个结点
                    # 考虑回环，还需要一个游标拿到尾结点位置
                    # 这里直接将rear移动到最后即可
                    rear = self.__head
                    while rear.next != self.__head:
                        rear = rear.next
                    # 此时rear指向最后一个结点
                    self.__head = cur.next
                    # 回环
                    rear.next = self.__head
                else:
                    # 其他结点
                    pre.next = cur.next
                return
            else:
                # 移动游标
                pre = cur
                cur = cur.next
        # 退出循环时，cur指向最后一个结点
        if cur.elem == item:
            # 考虑只有一个结点
            if cur == self.__head:
                self.__head = None
            else:
                pre.next = cur.next