unity 两点间生成随机的贝塞尔曲线

效果如图：

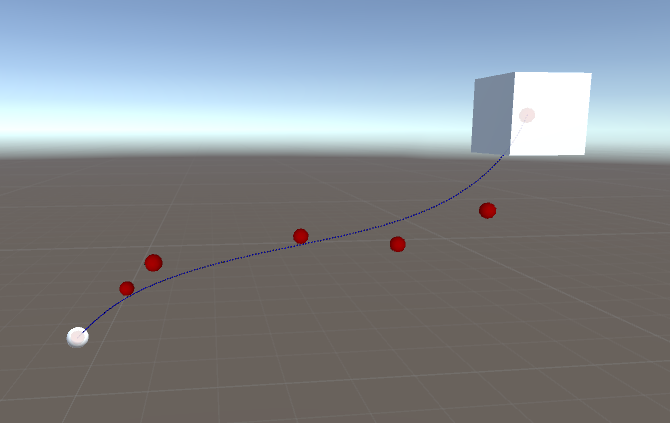
思路：

　　主要问题在于生成随机控制点。

　　1. 以start -> end 为z轴建立坐标系，获得 x_Axis, y_Axis, z_Axis

　　2.以z轴方向随机长度， x轴y轴随机所在位置

　　3.用贝塞尔曲线公式生成曲线

public class Test : MonoBehaviour
{
    public Transform m_Start;
    public Transform m_End;

    Vector3 m_AxisX;
    Vector3 m_AxisY;
    Vector3 m_AxisZ;
    float m_OriLength;

    List<Vector3> m_PointList;
    Vector3[] m_BLine;

    void Start()
    {
        m_PointList = new List<Vector3>();
        var start = m_Start.position;
        var end = m_End.position;
        m_OriLength = Vector3.Distance(start, end);

        BuildMoveMatrix(start, end);

        m_PointList.Add(start);
        RandomPoint(start, end, m_OriLength);
        m_PointList.Add(end);

        m_BLine = Bezeir.draw_bezier_curves(m_PointList.ToArray(), m_PointList.Count, 0.005f);
    }

    void BuildMoveMatrix(Vector3 start, Vector3 end)
    {
        var z = (end - start).normalized;
        var y = new Vector3(1.0f, 1.0f, -(z.x + z.y) / z.z).normalized;
        var x = Vector3.Cross(z, y).normalized;

        m_AxisX = x;
        m_AxisY = y;
        m_AxisZ = z;
    }

    void RandomPoint(Vector3 start, Vector3 end, float length)
    {
        if (length < m_OriLength * 0.3f)
            return;

        var len = UnityEngine.Random.Range(length * 0.2f, length * 0.8f);
        var point = (end - start).normalized * len + start;
        point = point + 
                m_AxisX * UnityEngine.Random.Range(-0.3f * length, 0.3f * length) + 
                m_AxisY * UnityEngine.Random.Range(-0.3f * length, 0.3f * length);

        RandomPoint(start, point, Vector3.Distance(start, point));
        m_PointList.Add(point);
        RandomPoint(point, end, Vector3.Distance(point, end));
    }
}

public class Bezeir
{
    public static Vector3[] draw_bezier_curves(Vector3[] points, int count, float step)
    {
        List<Vector3> bezier_curves_points = new List<Vector3>();
        float t = 0F;
        do
        {
            var temp_point = bezier_interpolation_func(t, points, count);    // 计算插值点
            t += step;
            bezier_curves_points.Add(temp_point);
        }
        while (t <= 1 && count > 1);    // 一个点的情况直接跳出.
        return bezier_curves_points.ToArray();  // 曲线轨迹上的所有坐标点
    }

    /// <summary>
    /// n阶贝塞尔曲线插值计算函数
    /// 根据起点，n个控制点，终点 计算贝塞尔曲线插值
    /// </summary>
    /// <param name="t">当前插值位置0~1 ，0为起点，1为终点</param>
    /// <param name="points">起点，n-1个控制点，终点</param>
    /// <param name="count">n+1个点</param>
    /// <returns></returns>
    private static Vector3 bezier_interpolation_func(float t, Vector3[] points, int count)
    {
        var PointF = new Vector3();
        var part = new float[count];
        float sum_x = 0, sum_y = 0, sum_z = 0;
        for (int i = 0; i < count; i++)
        {
            ulong tmp;
            int n_order = count - 1;    // 阶数
            tmp = calc_combination_number(n_order, i);
            sum_x += (float)(tmp * points[i].x * Math.Pow((1 - t), n_order - i) * Math.Pow(t, i));
            sum_y += (float)(tmp * points[i].y * Math.Pow((1 - t), n_order - i) * Math.Pow(t, i));
            sum_z += (float)(tmp * points[i].z * Math.Pow((1 - t), n_order - i) * Math.Pow(t, i));
        }
        PointF.x = sum_x;
        PointF.y = sum_y;
        PointF.z = sum_z;
        return PointF;
    }

    /// <summary>
    /// 计算组合数公式
    /// </summary>
    /// <param name="n"></param>
    /// <param name="k"></param>
    /// <returns></returns>
    private static ulong calc_combination_number(int n, int k)
    {
        ulong[] result = new ulong[n + 1];
        for (int i = 1; i <= n; i++)
        {
            result[i] = 1;
            for (int j = i - 1; j >= 1; j--)
                result[j] += result[j - 1];
            result[0] = 1;
        }
        return result[k];
    }

}


参考链接 ： https://blog.csdn.net/qq_32688731/article/details/84037072