jzoj3865[JSOI2014]士兵部署

‘

数据范围:n,m<=10^5,传送门:https://jzoj.net/senior/#main/show/3865

感觉jzoj好高明啊,就是访问不太稳定.

首先题意中被n个点控制的区域相当于这n个点组成的凸包.那么题意相当于m次询问这n个点的点集在加入一个点后的凸包面积.每次加入一个点之后的凸包至少不会比原来n个点组成的凸包小,因此我们先使用Graham扫描法在nlogn时间内求出原先n个点的凸包.

考虑加入一个点后凸包面积的变化.如果这个点在凸包内,那么面积不变.否则,这个点将位于新的凸包上,并且使得原凸包的连续一段不再出现在凸包上（即过这个点作凸包的切线）.注意新凸包的面积总可以表示为原凸包上连续的一段顶点之间的叉积再加上新加入的点和两个原凸包上的点的叉积,为了快速求取面积,需要预处理叉积的前缀和.

新加入的点的位置以及过这个点的凸包切线都可以通过二分求得.总复杂度O（nlogn+mlogn)，具体实现时可以找凸包的一个顶点,从这里出发将凸包和整个平面剖分成几部分,以此确定新加入的点的位置并分类讨论求解。

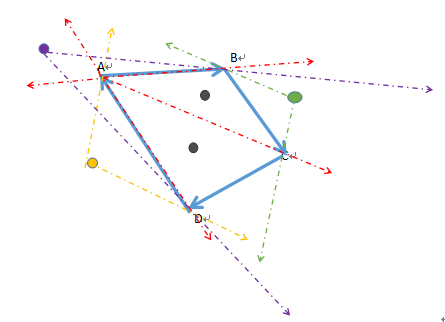
可以参照下图进行理解，蓝色实线为原先的凸包,以左上的点A为中心进行区域的分割,红色虚线为区域的边界线,黑色的点加入后不会影响凸包的面积,彩色的点加入后会影响凸包的面积,切线用对应颜色的虚线标出.

吐槽：本来是可以1A的，结果我怕共线出事对所有点的坐标随机扰动了一下就炸精度了....不随机扰动就A了....数据比较良心,似乎并没有所有点共线的情况(没有特殊处理也过了)

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=100005;
const double eps=1e-8;
int cmp(double x){return x<-eps?-1:x>eps;}
int seed;
int nxt_rand(){
  return 10;
  seed=(seed*7+3)%23;
  return seed;
}
struct point{
  double x,y;
  point(){}
  point(double a,double b){x=a;y=b;}
  void read(){scanf("%lf%lf",&x,&y);}
  bool operator <(const point &B)const{
    return cmp(x-B.x)==0?cmp(y-B.y)==-1:cmp(x-B.x)==-1;
  }
}P[maxn];
point operator +(const point &A,const point &B){return point(A.x+B.x,A.y+B.y);}
point operator -(const point &A,const point &B){return point(A.x-B.x,A.y-B.y);}
double cross(const point &A,const point &B){return A.x*B.y-A.y*B.x;}
point S[maxn];int top=0;
int n,m;
void ConvexHull(){
  for(int i=0;i<n;++i){
    while(top>1&&cmp(cross(S[top-1]-S[top-2],P[i]-S[top-2]))>=0)top--;
    S[top++]=P[i];
  }
  int lim=top;
  for(int i=n-2;i>=0;--i){
    while(top>lim&&cmp(cross(S[top-1]-S[top-2],P[i]-S[top-2]))>=0)top--;
    S[top++]=P[i];
  }
  top--;
}
bool inside(point C){
  return cmp(cross(C-S[0],S[1]-S[0]))>=0&&cmp(cross(S[top-1]-S[0],C-S[0]))>=0;
}
int binary1(int l,int r,point C){
  while(l<=r){
    int mid=(l+r)>>1;
    if(cmp(cross(S[mid]-S[mid-1],C-S[mid]))==1)r=mid-1;
    else l=mid+1;
  }
  return l-1;
}
int binary2(int l,int r,point C){
  while(l<=r){
    int mid=(l+r)>>1;
    if(cmp(cross(S[mid]-C,S[mid+1]-S[mid]))==1)l=mid+1;
    else r=mid-1;
  }
  return r+1;
}
double pre[maxn],suf[maxn];
int main(){
  //  for(int i=1;i<=100;++i)printf("%d
",nxt_rand());
  scanf("%d%d",&n,&m);
  for(int i=0;i<n;++i)P[i].read();
  if(n==1){
    for(int i=1;i<=m;++i)printf("0.0
");
  }else if(n==2){
    point C;
    for(int i=1;i<=m;++i){
      C.read();
      printf("%.1f
",fabs(cross(C-P[0],P[1]-P[0]))/2.0);
    }
  }else{
    sort(P,P+n);
    ConvexHull();
    for(int i=0;i<top;++i){
      pre[i]=suf[i]=cross(S[i],S[i+1]);
    }
    for(int i=1;i<top;++i)pre[i]+=pre[i-1];
    for(int i=top-2;i>=0;--i)suf[i]+=suf[i+1];
    point C;
    double ori=fabs(pre[top-1])/2.0;
    for(int i=1;i<=m;++i){
      C.read();
      if(inside(C)){
    int l=2,r=top-1;
    while(l<=r){
      int mid=(l+r)>>1;
      if(cmp(cross(S[mid]-S[0],C-S[0]))==1){
        r=mid-1;
      }else{
        l=mid+1;
      }
    }
    int pos=r+1;
    if(cmp(cross(S[pos]-S[pos-1],C-S[pos-1]))<=0){
      printf("%.1f
",ori);
    }else{
      int L=binary1(1,pos-1,C),R=binary2(pos,top-1,C);
      double area=pre[L-1]+suf[R]+cross(S[L],C)+cross(C,S[R]);
      printf("%.1f
",fabs(area)/2.0);
    }
      }else if(cmp(cross(C-S[0],S[1]-S[0]))==1){
    int L=0,R;
    int l=1,r=top-1;
    while(l<=r){
      int mid=(l+r)>>1;
      if(cmp(cross(S[mid+1]-S[mid],C-S[mid]))==-1){
        l=mid+1;
      }else{
        r=mid-1;
      }
    }
    R=r+1;
    double area=pre[R-1]+cross(S[R],C)+cross(C,S[0]);
    printf("%.1f
",fabs(area)/2.0);
      }else if(cmp(cross(C-S[0],S[top-1]-S[0]))==-1){
    int L=0,R;
    int l=1,r=top-1;
    while(l<=r){
      int mid=(l+r)>>1;
      if(cmp(cross(S[mid]-S[mid-1],C-S[mid-1]))==1)l=mid+1;
      else r=mid-1;
    }
    R=l-1;
    double area=cross(S[0],C)+cross(C,S[R])+suf[R];
    printf("%.1f
",fabs(area)/2.0);
      }else{
    int L=0,R=0;
    int l=1,r=top-1;
    while(l<=r){
      int mid=(l+r)>>1;
      if(cmp(cross(S[mid]-S[mid-1],C-S[mid-1]))==1)l=mid+1;
      else r=mid-1;
    }
    L=l-1;
    l=0;r=top-2;
    while(l<=r){
      int mid=(l+r)>>1;
      if(cmp(cross(S[mid+1]-S[mid],C-S[mid]))==1)r=mid-1;
      else l=mid+1;
    }
    R=r+1;
    double area=pre[R-1]-pre[L-1]+cross(C,S[L])+cross(S[R],C);
    printf("%.1f
",fabs(area)/2.0);
      }
    }
  }
  return 0;
}