Redis 产生背景
1.1.数据存储的发展史
1.1.1.磁盘时代
很久之前,我们的数据存储方式是磁盘存储,每个磁盘都有一个磁道。每个磁道有很多扇区,一个扇区接近512Byte。
磁盘的寻址速度是毫秒级的,带宽是GB/M的。内存是ns级的,带宽也比磁盘大上好几个数量级。总体来说,磁盘比内存在寻址上慢了接近10W倍。
在这段历史中,我们的面临的问题是,I/O问题。在读写文件时,我们常常面临很大的I/O成本问题。但是最初有个最初的解决方案是加一个buffer。
科普:什么是buffer?
buffer是指一个缓冲区,我们在缓冲区来进行一个暂时的存放,之后统一运输给内存,这样会使得I/O的性能有略微提升。
1.1.2.数据库的产生
任何技术都不会平白无故产生。
我们数据库技术就是由于磁盘的I/O瓶颈。为了解决这个问题,我们将磁盘扇区分为4K的一个个小的分区,构成索引。有了这些索引值,我们能通过索引,进行更加便捷的查找。为了我们能够更快的查找,我们将索引使用B+树进行存储。
科普:B+树是什么?
我们普通的1-0树,又称二叉查找树(二叉排序树),二叉查找树和排序树是同一种树,就是单纯的1-0树,按照中序遍历的存储方式进行从小到大(从大到小)进行存储。(初学者可能误以为两种树,包括我刚开始学习数据结构的时候)。
二叉查找树(二叉排序树)由于在插入和删除的时候,容易出现不太ok的情况,例如,可能在删除过程中删除为一个链表,这样查找效率依旧会变得很低。所以,我们使用旋转,通过左右旋转,将这种“链表”式(极端情况下)的树转化为左右平衡的树,这就是所谓的B-树。(注意误区,B树和B-树是一个树么?初学者认为后面一种是B减树,实际不是,是翻译过来的时候加的分隔符。B为Balance平衡的意思)
当然,我们的数据库文件不是二叉的,文件系统也不是,所以,我们多叉的查找树,就是所谓的B+树。+号代表每个节点不止二叉的意思。
(用自己的话粗略总结,详细还是看B-tree,B+tree的定义)
在我们数据库的查找中,我们遇到一个问题?那就是字节宽度问题。我们建库的时候必须给出schema,我们行级存储,即使是该列为空,依旧要占位,那么,数据量庞大的时候,将会浪费很大的存储空间。但是这样的好处是,我们可以在update的时候不需要移动数据的位置。
1.1.3.key-value数据库的产生
任何技术都不会平白无故产生。
我们将数据库发展到极致,产生出类似SAP公司的HANA数据库。这种数据库,硬件需求大,内存约2T,硬件软件服务总和约2亿一个套餐。
随着互联网的发展,我们面临了一个新的问题。如何才能抵挡高并发,以及大数据导致的查找变慢呢?(注意,数据量变大,仅仅影响多数据查找,单数据查找并不会影响性能。我们的业务逻辑,通常是多条数据查找,所以才会有瓶颈)
于是我们的k-v数据库产生了,这依赖于两个基础设施。冯诺依曼体系的硬件,以太网,和tcp/ip网络。参考附件:冯诺依曼体系图
科普:什么是冯诺依曼体系?
我们的操作系统老师是个年纪很大的教授,这边引用他的上课原话。
冯诺依曼体系,至今没有一个明确的定义。有的书说有5个,有的书说有7个,但是,我依照某年考研题,来规范一下冯诺依曼体系。
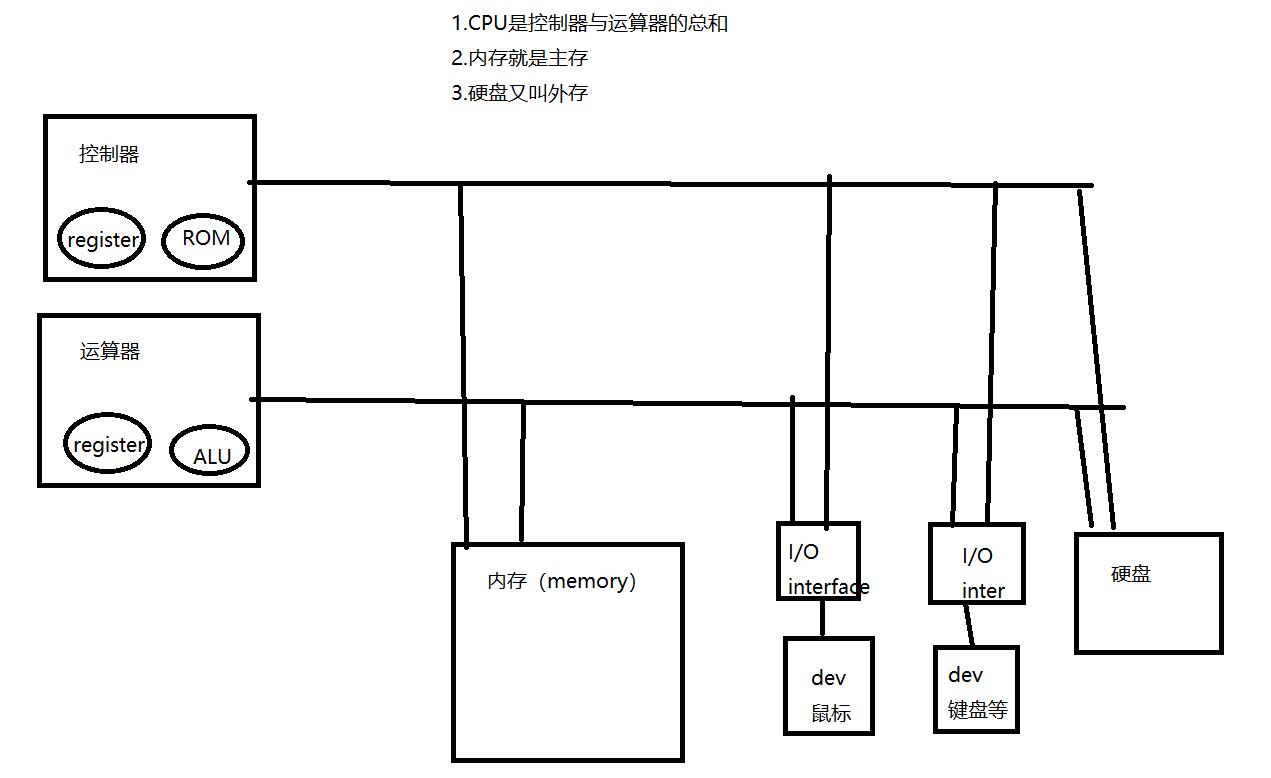
冯诺依曼体系由五部分组成,控制器,运算器,内存,总线,硬盘和I/O接口6部分组成。
(如何记忆冯诺依曼体系构成:CPU分为控制器运算器,其他都为CPU服务,运算需要内存,连接需要总线,我们要读写必须要I/O接口。一切以CPU考虑,就能记全6个)
参考附件:冯诺依曼体系图