\(AcWing\) \(247\). 亚特兰蒂斯
一、题目描述
有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。
其中一些甚至包括岛屿部分地图。
但不幸的是,这些地图描述了亚特兰蒂斯的不同区域。
您的朋友 \(Bill\) 必须知道地图的总面积。
你自告奋勇写了一个计算这个总面积的程序。
输入格式
输入包含多组测试用例。
对于每组测试用例,第一行包含整数 \(n\),表示总的地图数量。
接下来 \(n\) 行,描绘了每张地图,每行包含四个数字 \(x_1,y_1,x_2,y_2\)( 不一定是整数),(\(x_1,y_1\)) 和 (\(x_2,y_2\)) 分别是地图的左上角位置和右下角位置。
【注:这个左上和右下是与本题给的坐标系相关,不用过于纠结是左下+右上,还是左上+右下】
注意,坐标轴 \(x\) 轴从上向下延伸,\(y\) 轴从左向右延伸。
当输入用例 \(n=0\) 时,表示输入终止,该用例无需处理。
输出格式
每组测试用例输出两行。
第一行输出 Test case #k,其中 \(k\) 是测试用例的编号,从 \(1\) 开始。
第二行输出 Total explored area: a,其中 \(a\) 是总地图面积(即此测试用例中所有矩形的面积并,注意如果一片区域被多个地图包含,则在计算总面积时只计算一次),精确到小数点后两位数。
在每个测试用例后输出一个空行。
数据范围
\(1≤n≤10000, \\
0≤x_1<x_2≤100000, \\
0≤y_1<y_2≤100000\)
注意,本题 \(n\) 的范围上限加强至 \(10000\)。
输入样例:
2
10 10 20 20
15 15 25 25.5
0
输出样例:
Test case #1
Total explored area: 180.00
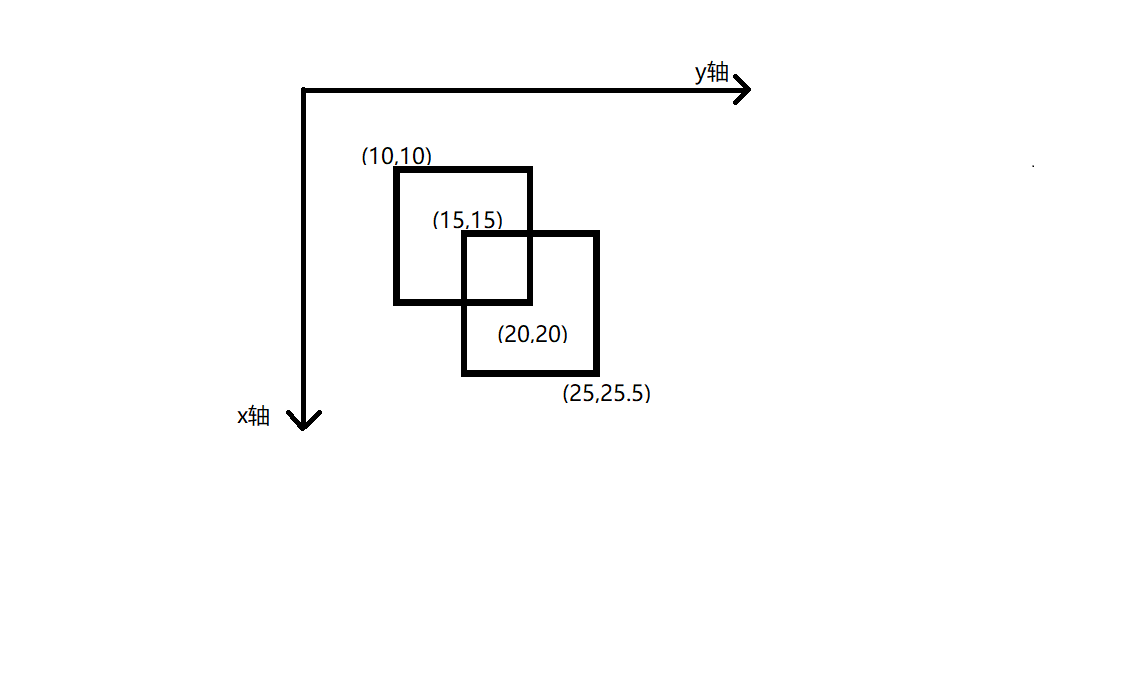
样例解释
样例所示地图覆盖区域如下图所示,两个矩形区域所覆盖的总面积,即为样例的解。
二、解题思路
这道题目不是特别严格的线段树,因为线段树维护的信息具有区间可合并性,这道题目想了很久想不出可以区间直接合并的信息。我们在这里维护的是 离散化后表示小段的数组,设为\(a[]\)吧,对于一个边界的两个纵坐标,设为\(y_1\)和\(y_2\),离散化后的结果为\([a_l,a_r]\),这是点,如果要对应到小段,那么则是\([a_l,a_{r−1}]\)。
在每个区间结点上,设\(cnt\)表示该区间被完整扫过的次数,这里强调下,是完整扫过,那些子区间被扫过但本身没被完整扫过的不能累加。因此,满足不了区间可合并的特性。但是因为在树上,我们在更新线段树的时候,可以将结果从下往上累加,在每个结点上用\(len\)表示该区间被扫描线覆盖的长度。下面是重
点:
当某个区间结点的\(cnt>0\),则\(tr[p].len=val[a_r+1] - val[a_l]\),因为线段树中维护的是小段,要计算的话,得转移到点上直接相减,所以右端点是\(a_{r} + 1\)。
当某个区间结点的\(cnt=0\),则它的\(len\)值是其左右儿子的\(len\)值之和。如果该点是叶结点,则\(len\)值重置为\(0\)。
该边界被扫描线覆盖的长度就是\(tr[1].len\)。不需要查询。事实上,这种做法下,查询了反而是错的。如果查询\([a_l,a_r]\),结果代表扫描线在区间\([a_l,a_r+1]\)被覆盖的长度,和要求不符,如果查询\([1,cnt−1]\),有可能该结点的\(cnt\)为\(0\),造成漏查。
根据以上分析,就无需下传标记了。
三、实现代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 100010;
struct Seg {
double x, y1, y2;
int k;
bool operator<(const Seg &t) const {
return x < t.x;
}
} seg[N << 1];
struct Node {
int l, r;
int cnt;
double len;
} tr[N << 2];
vector<double> ys; //用于离散化 ys:拼接映射的意思
//离散化+二分
int find(double y) {
return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}
void pushup(int u) {
if (tr[u].cnt)
tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
else if (tr[u].l == tr[u].r)
tr[u].len = 0;
else
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void modify(int u, int l, int r, int k) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].cnt += k;
pushup(u);
return;
}
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, k);
if (r > mid) modify(u << 1 | 1, l, r, k);
pushup(u);
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
int n, T = 1;
while (cin >> n, n) {
ys.clear(); //多组测试数组,每次清空离散化数组
for (int i = 1; i <= n; i++) {
double x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
seg[2 * i - 1] = {x1, y1, y2, 1};
seg[2 * i] = {x2, y1, y2, -1};
ys.push_back(y1);
ys.push_back(y2);
}
//离散化:y是小数,小数没法使用线段树,需要有映射的关系整数
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
//例子:假设现在有三个不同的y轴点,分为两个线段
// y[0] ~ y[1],y[1] ~ y[2];
//此时ys.size()为3,ys.size() - 2 为 1;
//此时为 build(1, 0, 1);
//有两个点0 和 1,线段树中0号点为y[0] ~ y[1],1号点为y[1] ~ y[2];
build(1, 0, ys.size() - 2); //实践证明,多开2个也没啥问题
sort(seg + 1, seg + 1 + 2 * n);
double res = 0;
for (int i = 1; i < n * 2; i++) {
modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k); // 真实坐标 -> 转换为 -> 离散化后的下标. 真实坐标是小数,不连续,离散化后,是整数而且连续
//坐标 映射 区间 办法= 以区间的开始编号为区间编号,类似于左闭右开
res += tr[1].len * (seg[i + 1].x - seg[i].x); //根结点的len * 阴影部分高度
}
printf("Test case #%d\n", T++);
printf("Total explored area: %.2lf\n\n", res);
}
return 0;
}