\(AcWing\) \(1228\). 油漆面积
一、题目大意
\(X\)星球的一批考古机器人正在一片废墟上考古。
该区域的地面坚硬如石、平整如镜。
管理人员为方便,建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。
它们感兴趣的内容也不相同。
经过各种测量,每个机器人都会报告一个或多个矩形区域,作为优先考古的区域。
矩形的表示格式为 \((x_1,y_1,x_2,y_2)\),代表矩形的两个对角点坐标。
为了醒目,总部要求对所有机器人选中的矩形区域 涂黄色油漆。
小明并不需要当油漆工,只是他需要计算一下,一共要耗费多少油漆。
其实这也不难,只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意,各个矩形间可能重叠。
输入格式
第一行,一个整数 \(n\),表示有多少个矩形。
接下来的 \(n\) 行,每行有 \(4\) 个整数 \(x_1,y_1,x_2,y_2\),空格分开,表示矩形的两个对角顶点坐标。
输出格式
一行一个整数,表示矩形覆盖的总面积。
数据范围
\(1≤n≤10000,0≤x_1,x_2,y_2,y_2≤10000\)
数据保证 \(x_1<x_2\) 且 \(y_1<y_2\)。
二、扫描线
对于这种题我们的正解就是 线段树 套 扫描线,听起来是不是逼格很高。
扫描线概念
扫描线可以想象成一根假想的线,将图
- ① 从左往右
- ② 从右往左
- ③ 自下而上
- ④ 自上而下
挑一种方式 扫描一遍,至于扫描的是什么则根据具体应用选择。
扫描线可以计算 矩形面积、周长,可以计算 线段交点,可以实现 多边形扫描转换,在图的处理方面经常用到。
这里总结一下 扫描线计算矩形面积 的算法。
【TODO,扫描线计算矩阵周长是不是也得练习一下?】
首先,对于之前的图,除了用总面积减去重合面积,还可以换一种计算方法,如图:
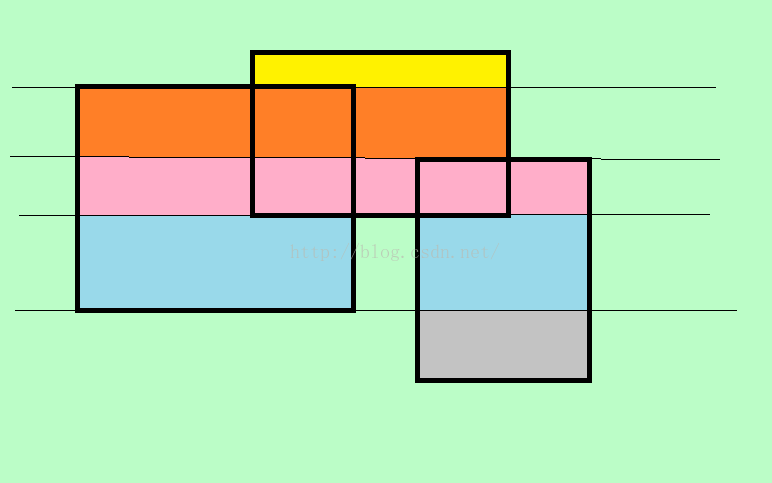
此图用\(4\)条横线将整个图划分成了\(5\)个部分,显然此时再算面积就可以用各个颜色的部分求和。
想想,这样计算的整个过程:
假设我们的视线自下而上,首先,我们看到了最下面灰色矩形的下边,
用这个下边的长度乘以这条边和上一条边的高度差即得到灰色矩形面积,
继续看到蓝色的矩形的下边,虽然蓝色矩形有两个,但我们计算时自然会用结合律将两个矩形的下边加起来再去乘以同样的高,然后重复这样的操作,我们最终可以求得整个图形的面积。
扫描线的计算机实现
但是,这依旧是人做的,计算机要怎么实现呢?
首先的问题:怎么保存这些矩形?
从刚才的过程,我们不难发现,只需要 保存这张图里面的所有水平的边 即可。
对于每条边,它的属性有三个:
- 左右端点(横坐标)
- 高度(纵坐标)
- 这条边属于矩形的上边还是下边 (想想为什么保存这个属性)
线段树登场
刚刚计算中我们遇到两个蓝色矩形,一眼就能看出这两个蓝色矩形的 宽 是多少,用计算机怎么做到?
我们以整个图最左边的竖线作为区间左端点,最右边的竖线作为区间右端点,去维护这个区间的有效长度(即被覆盖的长度) \(1\sim n\)
比如扫到第\(2\)条边的时候,有效长度就是两个蓝色矩形的宽之和。
这样,我们用扫描线去扫描每一条边的时候,都需要更新线段树的 有效长度
如何更新呢?
如果扫到的这条边是某矩形的 下边,则往区间 插入这条线段
如果扫到的这条边是某矩形的 上边,则往区间 删除这条线段
为什么?自己试着模拟一下就不难发现:
因为我们是自下而上的扫这个图,扫到下边相当于刚刚进入一个矩形,扫到上边则是要离开一个矩形
利用线段树把每条边的有效长度找到了,也就是找到了每部分的所有矩形的总宽,那么高呢?
高就简单多了,对于所有的边, 按照高度从小到大排列, 那么矩形高就是每相邻边之间的 高度差
三、实现代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e4 + 10;
struct Seg {
int x, y1, y2, k;
bool operator<(const Seg &t) const {
return x < t.x;
}
} seg[N << 1];
/*
扫描线题型中,线段树这个数据结构维护的仍然是一段段区间,也就是边,比如:
第1点 ~ 第3点 => 第 1 条边, 第 2 条边
...
点p1~ 点p2 => 第p1条边 ~ 第p2-1条边
线段树各个区间是不能存在交叉的!!比如 一维数组 a[]={1,2,3,4,5,6},对应的线段树,也肯定是没有一个节点管辖范围不清,存在重复的。
但对于坐标而言,比如(y1,y2),(y2,y3),就可能有问题出现。因为y2到底是属于哪个爹管辖?不能两爹都管辖吧???就像上面的栗子一样,是第一个爹管辖y1~y2-1,第二个爹管辖y2~y3-1,理解为
第几号边。
这样就造成了一个坐标和线段树中维护区间的对应关系,=> [y1,y2) =[y1,y2-1]
同时,也使得在计算区间长度时,还需要加1进行补偿:tr[u].len = tr[u].r - tr[u].l + 1;
*/
struct Node {
int l, r;
int cnt; //被覆盖次数
int len; //有效长度
} tr[N << 2];
void pushup(int u) {
//结点区间被覆盖过一次以上,len就等于区间长度
//+1是因为线段树的叶节点是单位线段,而不是点,比如区间包含单位线段1和单位线段2,len=2-1+1=2
if (tr[u].cnt) tr[u].len = tr[u].r - tr[u].l + 1;
//否则递归下去,终止条件:当l==r表示是一条单位线段,且没被覆盖(else),所以len=0
else if (tr[u].l == tr[u].r)
tr[u].len = 0;
//不是叶节点len=两个子节点的len之和
else
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void modify(int u, int l, int r, int k) {
if (l <= tr[u].l && r >= tr[u].r) {
tr[u].cnt += k;
pushup(u);
return;
}
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, k);
if (r > mid) modify(u << 1 | 1, l, r, k);
pushup(u);
}
int n, idx;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
seg[++idx] = {x1, y1, y2, 1};
seg[++idx] = {x2, y1, y2, -1};
}
sort(seg + 1, seg + 1 + idx);
build(1, 0, 10000); // 0<=y1<y2<=10000
int ans = 0;
for (int i = 1; i < idx; i++) {
modify(1, seg[i].y1, seg[i].y2 - 1, seg[i].k);
ans += tr[1].len * (seg[i + 1].x - seg[i].x);
}
printf("%d\n", ans);
return 0;
}