Using Threads for Parallelism
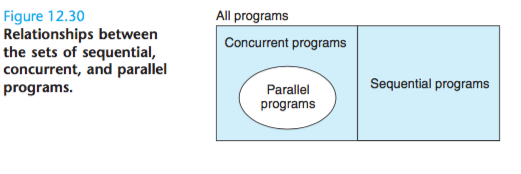
Figure 12.30 shows the set relationships between sequential, concurrent, and parallel programs.
A parallel program is a concurrent program running on multiple processors.
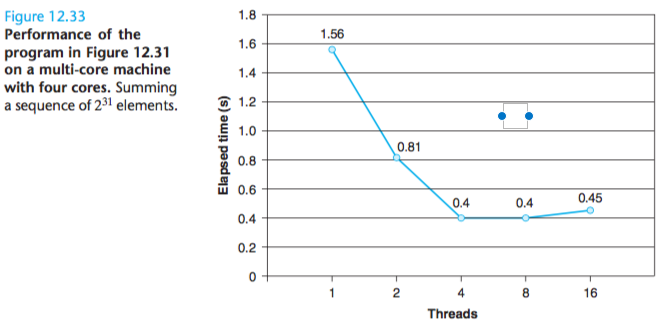
Running time actually increases a bit as we increase the number of threads because of the overhead of context switching multiple threads on the same core.
The speedup of a parallel program is typically defined as
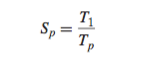
where p is the number of processor cores and Tk is the running time on k cores.
When T1 is the execution time of a sequential version of the program, then Sp is called the absolute speedup.
When T1 is the execution time of the parallel version of the program running on one core, then Sp is called the relative speedup.
Absolute speedup is a truer mea- sure of the benefits of parallelism than relative speedup.
Parallel programs often suffer from synchronization overheads, even when they run on one processor, and these overheads can artificially inflate the relative speedup numbers because they increase the size of the numerator.
On the other hand, absolute speedup is more difficult to measure than relative speedup because measuring absolute speedup requires two different versions of the program.
A related measure, known as efficiency, is defined as
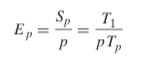
and is typically reported as a percentage in the range (0, 100].Efficiency is a mea- sure of the overhead due to parallelization.
Programs with high efficiency are spending more time doing useful work and less time synchronizing and commu- nicating than programs with low efficiency.
There is another view of speedup, known as weak scaling, which increases the problem size along with the number of processors, such that the amount of work performed on each processor is held constant as the number of processors increases.
Other Concurrency Issues
Thread Safety
A function is said to be thread-safe if and only if it will always produce correct results when called repeatedly from multiple concurrent threads.
We can identify four (nondisjoint) classes of thread-unsafe functions:
Class 1: Functions that do not protect shared variables.
This class of thread-unsafe function is relatively easy to make thread-safe: protect the shared variables with synchronization operations such as P and V .
An advantage is that it does not require any changes in the calling program. A disadvantage is that the synchronization operations will slow down the function.
Class 2: Functions that keep state across multiple invocations.
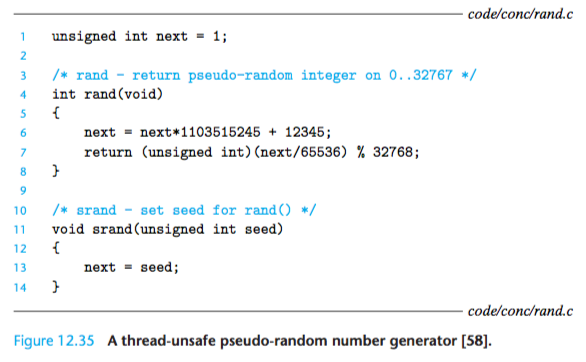
Consider the pseudo-random number generator package in Fig- ure 12.35.
The rand function is thread-unsafe because the result of the current invocation depends on an intermediate result from the previous iteration.
When we call rand repeatedly from a single thread after seeding it with a call to srand, we can expect a repeatable sequence of numbers.
However, this assumption no longer holds if multiple threads are calling rand.
The only way to make a function such as rand thread-safe is to rewrite it so that it does not use any static data, relying instead on the caller to pass the state information in arguments.
The disadvantage is that the programmer is now forced to change the code in the calling routine as well.
In a large program where there are potentially hundreds of different call sites, making such modifications could be nontrivial and prone to error.
Class 3: Functions that return a pointer to a static variable.
Some functions, such as ctime and gethostbyname, compute a result in a static variable and then return a pointer to that variable.
If we call such functions from concurrent threads, then disaster is likely, as results being used by one thread are silently overwritten by another thread.
There are two ways to deal with this class of thread-unsafe functions.
One option is to rewrite the function so that the caller passes the address of the variable in which to store the results.
This eliminates all shared data, but it requires the programmer to have access to the function source code.
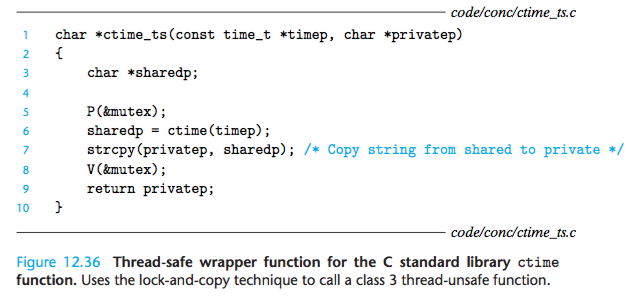
If the thread-unsafe function is difficult or impossible to modify (e.g., the code is very complex or there is no source code available), then another option is to use the lock-and-copy technique.
The basic idea is to associate a mutex with the thread-unsafe function.
At each call site, lock the mutex, call the thread-unsafe function, copy the result returned by the function to a private memory location, and then unlock the mutex.
To minimize changes to the caller, you should define a thread-safe wrapper function that performs the lock-and-copy, and then replace all calls to the thread-unsafe function with calls to the wrapper.
For example, Figure 12.36 shows a thread-safe wrapper for ctime that uses the lock-and-copy technique.
Class 4: Functions that call thread-unsafe functions.
If a function f calls a thread-unsafe function g, is f thread-unsafe? It depends.
If g is a class 2 function that relies on state across multiple invocations, then f is also thread- unsafe and there is no recourse short of rewriting g.
However, if g is a class 1 or class 3 function, then f can still be thread-safe if you protect the call site and any resulting shared data with a mutex.
We see a good example of this in Figure 12.36, where we use lock-and-copy to write a thread-safe function that calls a thread-unsafe function.
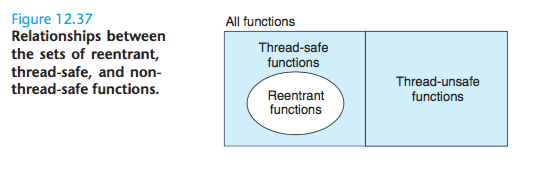
Reentrancy
There is an important class of thread-safe functions, known as reentrant functions, that are characterized by the property that they do not reference any shared data
when they are called by multiple threads.
Reentrant functions are typically more efficient than nonreentrant thread- safe functions because they require no synchronization operations.
Furthermore, the only way to convert a class 2 thread-unsafe function into a thread-safe one is to rewrite it so that it is reentrant.
For example, Figure 12.38 shows a reentrant version of the rand function from Figure 12.35.
The key idea is that we have replaced the static next variable with a pointer that is passed in by the caller.

Is it possible to inspect the code of some function and declare a priori that it is reentrant? Unfortunately, it depends.
If all function arguments are passed by value (i.e., no pointers) and all data references are to local automatic stack variables (i.e., no references to static or global variables), then the function is explicitly reentrant,
in the sense that we can assert its reentrancy regardless of how it is called.
However, if we loosen our assumptions a bit and allow some parameters in our otherwise explicitly reentrant function to be passed by reference (that is, we allow them to pass pointers) then we have an implicitly reentrant function,
in the sense that it is only reentrant if the calling threads are careful to pass pointers to nonshared data. For example, the rand_r function in Figure 12.38 is implicitly reentrant.
We always use the term reentrant to include both explicit and implicit reen- trant functions.
However, it is important to realize that reentrancy is sometimes a property of both the caller and the callee, and not just the callee alone.
//TODO exercise
Using Existing Library Functions in Threaded Programs
However, the lock-and-copy approach has a number of disadvantages.
First, the additional synchronization slows down the program.
Second, functions such as gethostbyname that return pointers to complex struc- tures of structures require a deep copy of the structures in order to copy the entire structure hierarchy.
Third, the lock-and-copy approach will not work for a class 2 thread-unsafe function such as rand that relies on static state across calls.
Therefore, Unix systems provide reentrant versions of most thread-unsafe functions.
The names of the reentrant versions always end with the “_r” suffix. For example, the reentrant version of gethostbyname is called gethostbyname_r.
We recommend using these functions whenever possible.
Races
Races usually occur because programmers assume that threads will take some particular trajec- tory through the execution state space, forgetting the golden rule that threaded programs must work correctly for any feasible trajectory.
Deadlocks
Semaphores introduce the potential for a nasty kind of run-time error, called deadlock, where a collection of threads are blocked, waiting for a condition that will never be true.
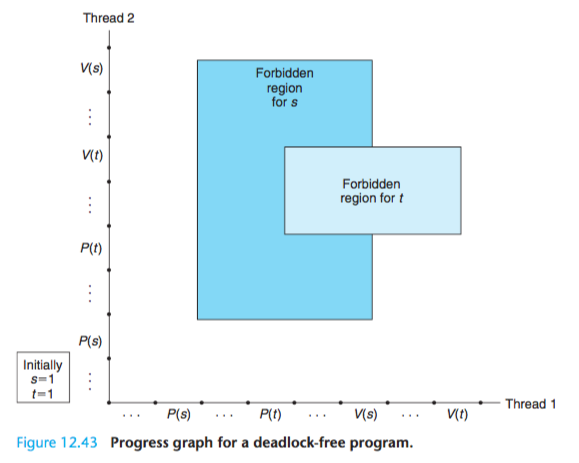
Figure 12.42 shows the progress graph for a pair of threads that use two semaphores for mutual exclusion.
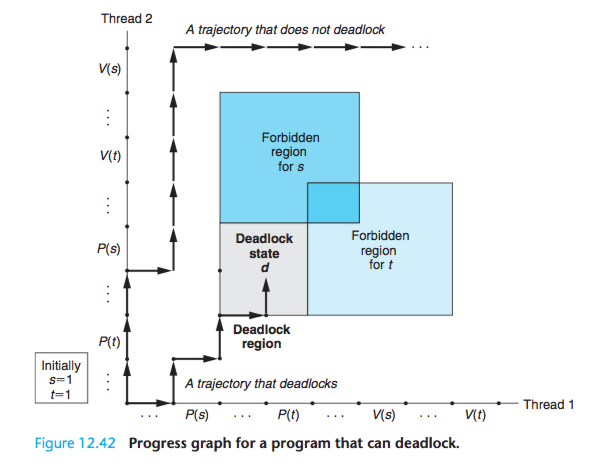
From this graph, we can glean some important insights about deadlock:
(1)The programmer has incorrectly ordered the P and V operations such that the forbidden regions for the two semaphores overlap.
If some execution trajectory happens to reach the deadlock state d, then no further progress is possible because the overlapping forbidden regions block progress in every legal direction.
In other words, the program is deadlocked because each thread is waiting for the other to do a V operation that will never occur.
(2)The overlapping forbidden regions induce a set of states called the deadlock region.
If a trajectory happens to touch a state in the deadlock region, then deadlock is inevitable. Trajectories can enter deadlock regions, but they can never leave.
(3) Deadlock is an especially difficult issue because it is not always predictable.
However, when binary semaphores are used for mutual exclusion, as in Figure 12.42, then you can apply the following simple and effective rule to avoid deadlocks:
Mutex lock ordering rule:
A program is deadlock-free if, for each pair of mutexes (s, t) in the program, each thread that holds both s and t simultaneously locks them in the same order.
For example, we can fix the deadlock in Figure 12.42 by locking s first, then t in each thread. Figure 12.43 shows the resulting progress graph.