分析
将原问题做如下转化:
总钱数相当于背包总容量;
每件物品的价格相当于体积;
每件物品的价格乘以重要度相当于价值;
那么就变成了经典的\(01\)背包问题。
01背包模型
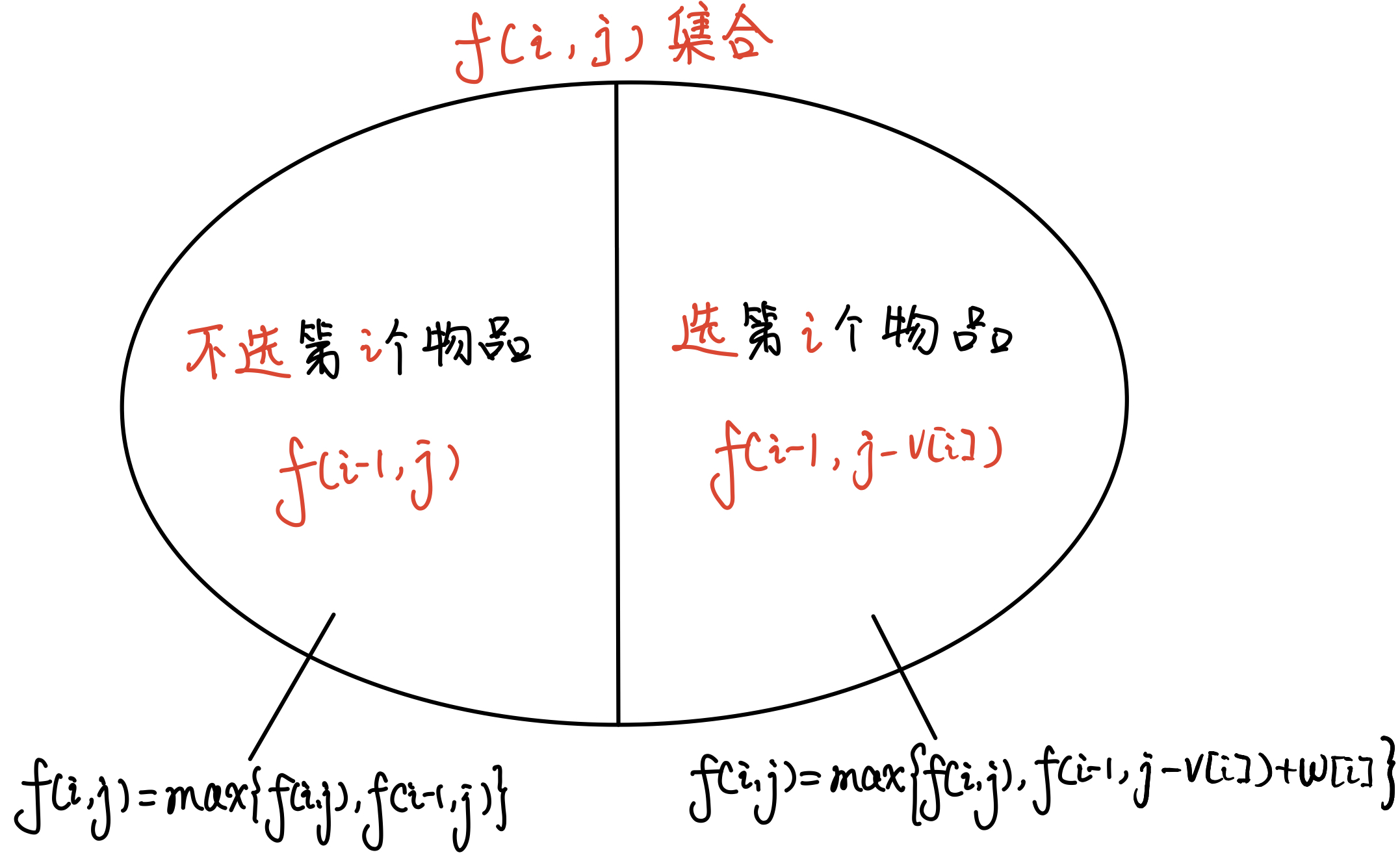
状态表示\(f(i,j)\)—集合: 考虑前 \(i\) 个物品,且当前已使用体积为$ j$ 的方案
状态表示\(f(i,j)\)—属性: 该方案的价值为最大值 \(max\)
状态转移\(f(i,j)\): \(f(i,j)=\begin{equation} \left\{ \begin{array}{lr} 不选第i个物品: max\{f(i-1,j)\} & \\ 选第i个物品: max\{f(i-1,j-v_i)+w_i\}\\ \end{array} \right. \end{equation}\)
初始状态:f[0][0]
目标状态:f[n][m]
集合划分
#include<bits/stdc++.h>
using namespace std;
const int N = 30010;
int n, m;
int f[N];
int main() {
//物品个数n
cin >> m >> n;//注意一下这里输入的顺序
//01背包模板
for (int i = 1; i <= n; i++) {
int v, w;
cin >> v >> w;
for (int j = m; j >= v; j--)
f[j] = max(f[j], f[j - v] + v * w);
}
cout << f[m] << endl;
return 0;
}