AcWing 905. 区间选点

题目传送门

一、题目解读

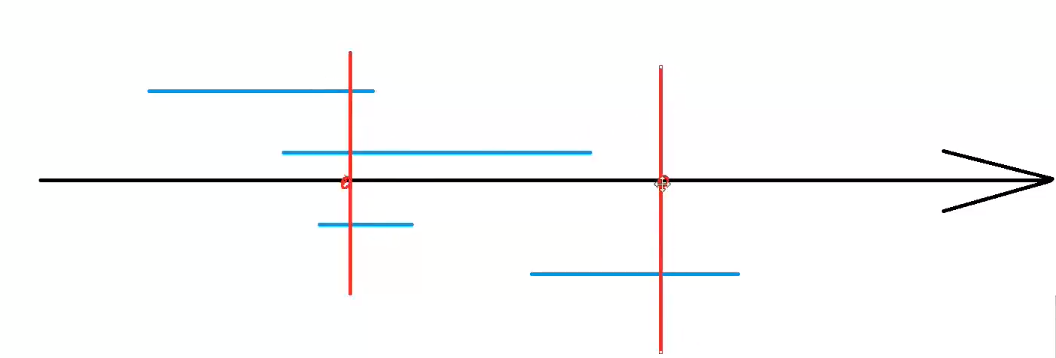
(1)每个线段上最少要选择一个点。

(2)如果一个点同时出现在两个线段上，就可以节约掉一个点。

给我们(N)个区间，问我们最少可以选择几个点。比如上图，就是可以选择两个点。

二、解题思路

贪心问题，区间问题无外乎就是排序，
（1）按左端点排序

（2）按右端点排序

（3）双关键字排序（先按右端点，再按左端点）

如果没有思路就先试一下，举一些例子，感受一下是不是有问题，看看有什么规律没有。

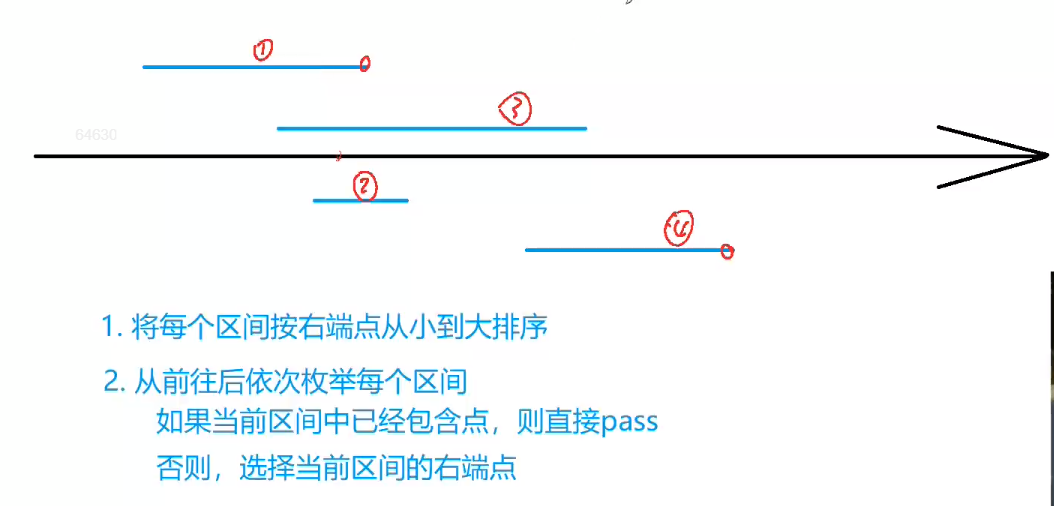
(Q):为啥要按右端点排序呢？
A:选择右端点，就是想获取到本个线段的最大可以达到哪个位置，能获得最大的利益（越靠后，当然选择点的个数就会越少了。）

三、实现代码

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int n;   //线段数量
int res; //结果
int ed = -INF; //当前覆盖区间的结束边界，即右端点位置

//结构体
struct Range {
    int l, r;
} range[N];

//强制要求使用这种结构体的排序自定义函数方式
//按每个区间的右端点从小到大排序
bool cmp(const Range &a, const Range &b) {
    return a.r < b.r;
}

int main() {
    //优化输入
    ios::sync_with_stdio(false);
    cin >> n;
    //注意这里的数组下标是从1开始的
    for (int i = 1; i <= n; i++) cin >> range[i].l >> range[i].r;

    //右端点从小到大排序，排序也需要从数组下标1开始
    sort(range + 1, range + n + 1, cmp);

    //思想：按右端点从小到大排序后，再遍历每一个区间，尽可能取右端点，如果中间出现中断现象，只能再多一个点
    //其实，每一个点都可能有多个选择，只要是多个区间的共同点即可，不是唯一点
    for (int i = 1; i <= n; i++)
        if (range[i].l > ed) {
            res++;
            ed = range[i].r;
        }
    printf("%d
", res);
    return 0;
}