P1228 地毯填补问题题解

题目传递门

非常经典的棋盘覆盖问题，一定要和有学识的老师学习，事半功倍啊：分治法之棋盘覆盖——东北大学

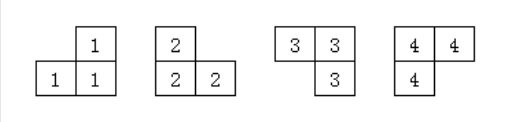
四种地毯的形状：

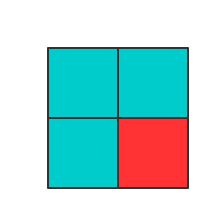
首先考虑(2 imes 2)的情况。假设这个特殊点在((2,2))，那么很明显正确的填法是这样的：

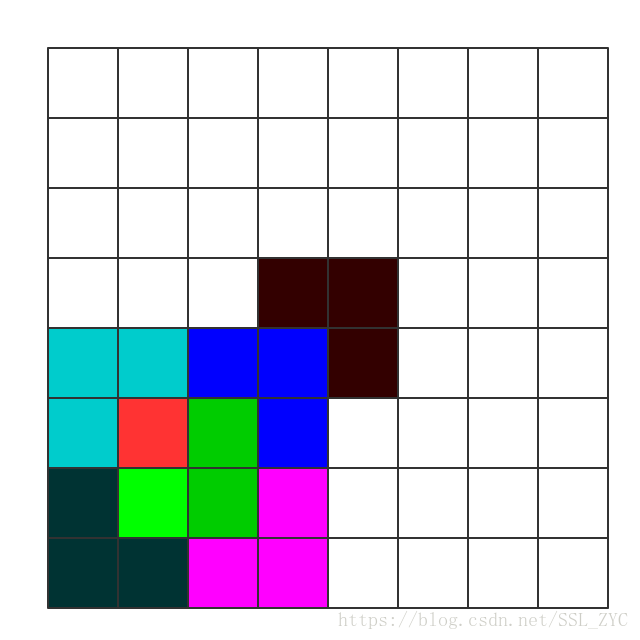
那么接下来就要扩大到(4 imes 4)了：

这时候，另外三个(2 imes 2)的未上色格子就没有特殊点了，也就没法像一开始的(2 imes 2)的格子做。那么可不可以给每个(2 imes 2)的格子都增加一个特殊点呢？

答案很明显是可以的。只要在四个(2 imes 2)的格子的正中间旁边的(3)个白色格子都填上同一种颜色，然后再分别处理三个(2 imes 2)的格子就可以！

那么再分别处理三个(2 imes 2)格子，得到

那么同理，当我们扩充到(8 imes 8)的格子时候，也用同样的方法，现将中间点旁边的白点标记为特殊点。

然后同理。。。

那么就可以推出(2^{10})大小的答案啦！

那么，如果要我们求(2^{10})大小的答案，那么就首先找到它的中点，判断特殊点在那边，然后就往那边递归，就变成(2^9 imes 2^9) 了，之后一直递归下去直到变成(2 imes 2)，然后就像上面说的一样慢慢染色输出啦！

c++代码

#include <bits/stdc++.h>

using namespace std;

//功能: 通过不断的判断公主的位置，完成对棋盘进行L形的填充,要求填充完整，不能有遗漏，不能冒出去棋盘。
//参数：棋盘左上，棋盘右下，公主位置
void dfs(int x1, int y1, int x2, int y2, int gz_x, int gz_y) {
    //变成了2*2(递归出口)
    if (x2 - x1 == 1 && y2 - y1 == 1) {
        //具体用哪号地毯，可以参考题解上方的地毯图形说明
        if (gz_x == x1 && gz_y == y1) printf("%d %d 1
", x2, y2); //公主在左上,1号地毯
        if (gz_x == x1 && gz_y == y2) printf("%d %d 2
", x2, y1); //公主在右上,2号地毯
        if (gz_x == x2 && gz_y == y1) printf("%d %d 3
", x1, y2); //公主在左下,3号地毯
        if (gz_x == x2 && gz_y == y2) printf("%d %d 4
", x1, y1); //公主在右下,4号地毯
        return;//最后一块铺完，Game Over~ 递归出口
    }

    //取出中心点,举个栗子：5~8，则(8-5)/2+5=6,就是5~8之间的中心点是6，靠近小的那边
    int mid_x = (x2 - x1) / 2 + x1;
    int mid_y = (y2 - y1) / 2 + y1;

    //接下来就是分治特殊点的位置，往那个方向搜索。
    if (gz_x <= mid_x && gz_y <= mid_y) {                               //公主在左上
        dfs(x1, y1, mid_x, mid_y, gz_x, gz_y);                          //递归左上角

        printf("%d %d 1
", mid_x + 1, mid_y + 1);               //放上去一个1号地毯，相当于构建了三个虚拟的公主
        dfs(mid_x + 1, y1, x2, mid_y, mid_x + 1, mid_y);                //左下角(虚拟公主在左下角的右上角)
        dfs(mid_x + 1, mid_y + 1, x2, y2, mid_x + 1, mid_y + 1);//右下角(虚拟公主在右下角的左上角)
        dfs(x1, mid_y + 1, mid_x, y2, mid_x, mid_y + 1);                //右上角(虚拟公主在右上角的左下角)
    }
    if (gz_x <= mid_x && gz_y > mid_y) { //右上
        dfs(x1, mid_y + 1, mid_x, y2, gz_x, gz_y);                    //递归右上角
        printf("%d %d 2
", mid_x + 1, mid_y);                     //放上去一个2号地毯，相当于构建了三个虚拟的公主
        dfs(x1, y1, mid_x, mid_y, mid_x, mid_y);                                 //左上角 (虚拟公主在左上角的右下角)
        dfs(mid_x + 1, y1, x2, mid_y, mid_x + 1, mid_y);                 //左下角 (虚拟公主在左下角的右上角)
        dfs(mid_x + 1, mid_y + 1, x2, y2, mid_x + 1, mid_y + 1); //右下角 (虚拟公主在右下角的左上角)
    }
    if (gz_x > mid_x && gz_y <= mid_y) { //左下
        dfs(mid_x + 1, y1, x2, mid_y, gz_x, gz_y);                      //递归左下角
        printf("%d %d 3
", mid_x, mid_y + 1);                       //放上去一个3号地毯，相当于构建了三个虚拟的公主
        dfs(mid_x + 1, mid_y + 1, x2, y2, mid_x + 1, mid_y + 1);    //右下角(虚拟公主在右下角的左上角)
        dfs(x1, y1, mid_x, mid_y, mid_x, mid_y);                                    //左上角(虚拟公主在左上角的右下角)
        dfs(x1, mid_y + 1, mid_x, y2, mid_x, mid_y + 1);                    //右上角(虚拟公主在右上角的左下角)
    }
    if (gz_x > mid_x && gz_y > mid_y) { //右下
        dfs(mid_x + 1, mid_y + 1, x2, y2, gz_x, gz_y);//递归右下角
        printf("%d %d 4
", mid_x, mid_y);                      //放上去一个4号地毯，相当于构建了三个虚拟的公主
        dfs(x1, y1, mid_x, mid_y, mid_x, mid_y);                               //左上角(虚拟公主在左上角的右下角)
        dfs(x1, mid_y + 1, mid_x, y2, mid_x, mid_y + 1);               //右上角(虚拟公主在右上角的左下角)
        dfs(mid_x + 1, y1, x2, mid_y, mid_x + 1, mid_y);               //左下角(虚拟公主在左下角的右上角)
    }
}

int main() {
    int x, y; //公主的位置
    int k;    //2^k是棋盘的大小
    cin >> k >> x >> y;
    //递归
    int n = 1 << k; //计算n=2^k,用位运算更快
    //开始铺地毯的坐标x1,y1;结束铺地毯的坐标x2,y2; 最后两个参数是公主的位置
    dfs(1, 1, n, n, x, y);
    return 0;
}