Description
zzy今天刚买了两个水瓢A和B,容量都是为1升,童心未泯的他打算用这个水瓢来玩游戏。
首先zzy准备了一个容量可看作无穷大的水缸,刚开始水缸是空的,然后用水瓢A往水缸里加水,用水瓢B把水缸里的水舀出去,当使用 水瓢B把水舀出去时水缸里必须要至少有1升的水。这样子使用N次水瓢A,也使用N次水瓢B,最后水缸会依旧空的。
Input
输入有多个例子,直到文件结束。
每个例子仅含一个数N(0<N<=10000),表示你必须使用N次A水瓢和N次B水瓢。
Output
对于每个例子,请输出一个数,表示一共有多少种正确的舀水方式使得舀水过程中 使用B水瓢时水缸里总会有足够的水。
(由于数字比较大,输出的答案模1000000007)
这道题是个水题,关键是判断出是进出栈这样一个模型。
进出栈满足卡特兰数,所以这道题等于是一个打表输出的过程
下面贴代码,也作为打表的模板。
1 #include<iostream> 2 #include<string.h> 3 #include<stdio.h> 4 #define mod 1000000007 5 #define maxn 10000+10 6 #define LL long long 7 LL C[maxn]; 8 using namespace std; 9 void built() 10 { 11 memset(C,0,sizeof(C)); 12 C[1]=1;C[2]=1;C[3]=1; 13 for (int i=4;i<maxn;i++) 14 { 15 for(int j=2;j<=i-1;j++) 16 { 17 C[i]+=((C[j]%mod)*(C[i+1-j]%mod))%mod; 18 } 19 C[i]=C[i]%mod; 20 } 21 return ; 22 } 23 int main() 24 { 25 built(); 26 int n; 27 while(~scanf("%d",&n)) 28 { 29 printf("%lld ",C[n+2]); 30 } 31 return 0; 32 }
递推的公式白书上有。
但鉴于个人的数学能力,我还是列举一些卡特兰数的模型。
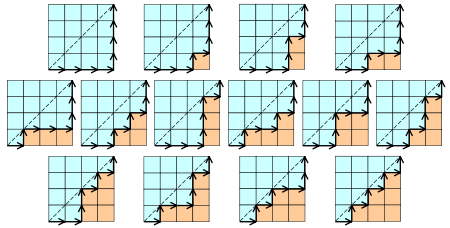
形式:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786.......
Description
zzy今天刚买了两个水瓢A和B,容量都是为1升,童心未泯的他打算用这个水瓢来玩游戏。
首先zzy准备了一个容量可看作无穷大的水缸,刚开始水缸是空的,然后用水瓢A往水缸里加水,用水瓢B把水缸里的水舀出去,当使用 水瓢B把水舀出去时水缸里必须要至少有1升的水。这样子使用N次水瓢A,也使用N次水瓢B,最后水缸会依旧空的。
Input
输入有多个例子,直到文件结束。
每个例子仅含一个数N(0<N<=10000),表示你必须使用N次A水瓢和N次B水瓢。
Output
对于每个例子,请输出一个数,表示一共有多少种正确的舀水方式使得舀水过程中 使用B水瓢时水缸里总会有足够的水。
(由于数字比较大,输出的答案模1000000007)