数据结构 题解

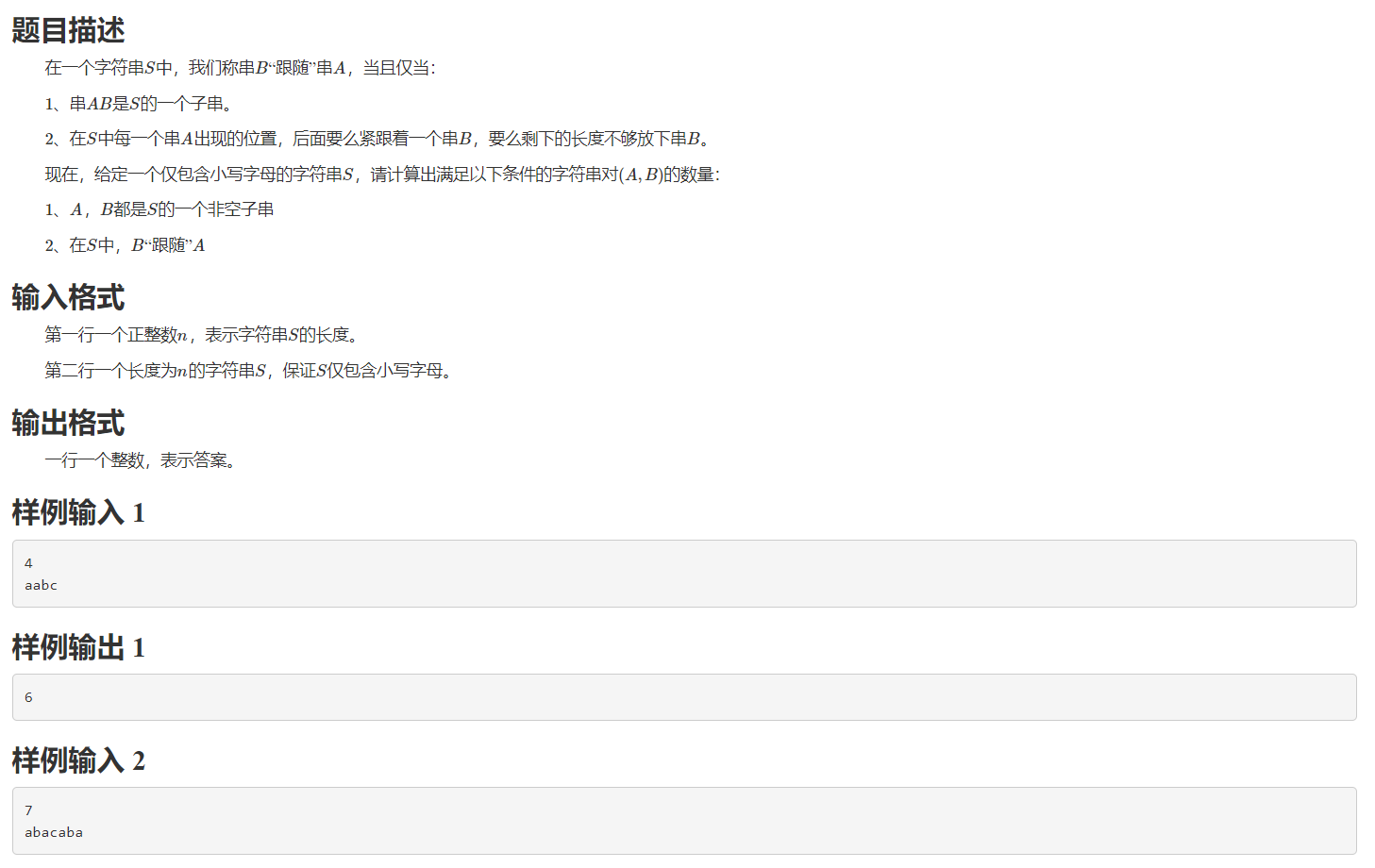
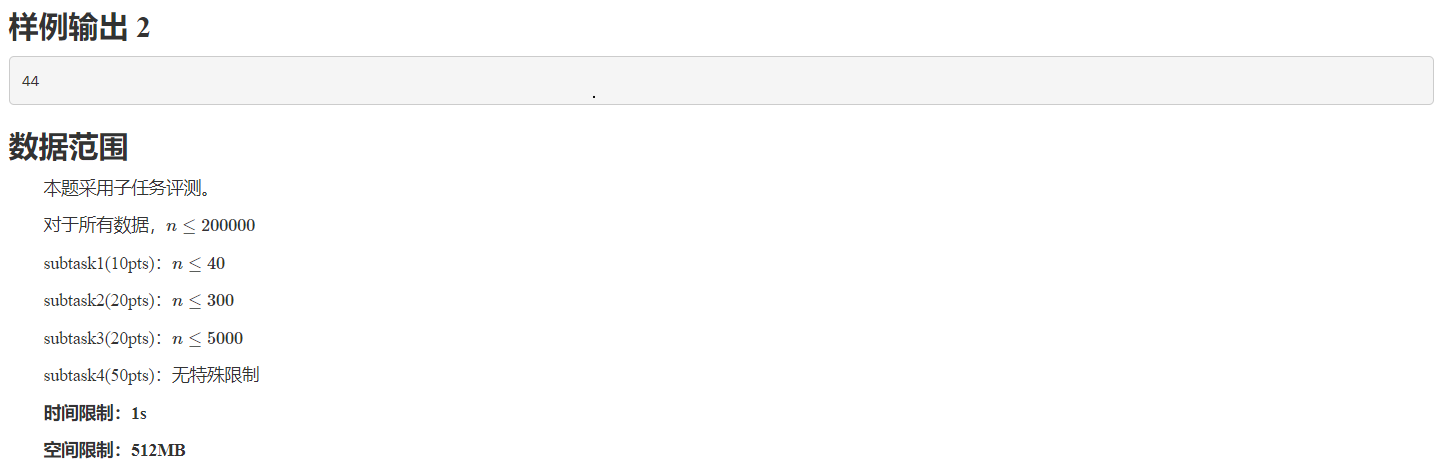
一、题目：

二、思路：

一道非常好的后缀树相关题目。

先贴一张后缀树的图片：

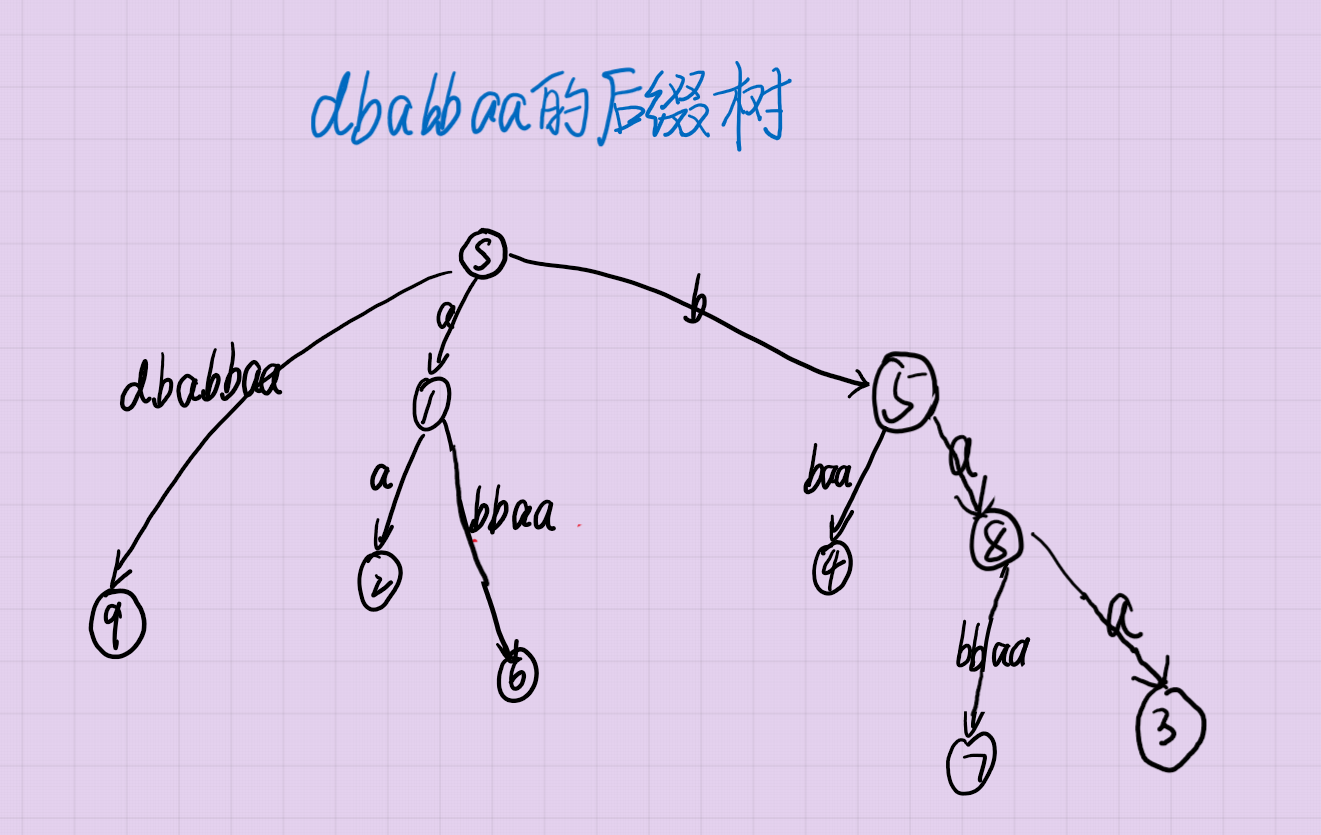
从根下来的一条路径所对应的子串都是不同的。

首先我们考虑后缀树上从父亲到某个儿子的一条边 ((x,y))，这条边肯定会包含若干个字母。举个例子，比如边 ((1,6)) 就包含了 (mathtt{bbaa}) 这四个字母。那么，如果 (A) 是后缀树从根下来，到这条边的某个字母所对应的子串，(B) 是这条边剩余的字母组成的子串，那么我们可以肯定，所有 (A) 出现过的位置后面一定跟的是 (B)。

比如就拿 ((1,6)) 边来举例子。那么就有

A	B
(mathtt{ab})	(mathtt{baa})
(mathtt{abb})	(mathtt{aa})
(mathtt{abba})	(mathtt{a})

假设一条边上字母的个数为 (len)，所以一条边可以贡献的答案就是 (1+2+cdots+len-1)，即 (dfrac{len imes(len - 1)}{2})。

但是这些还不够，题目中说，那些 (A) 后面不够 (B) 的长度的位置可以不管，也就是说，不一定必须要对于 (A) 出现的所有位置，(B) 都要跟在后面，允许一些位置后面不跟 (B)。这些 (A) 后面是可以跟不同的子串的，对应在后缀树上就是一个分叉点把 (A) 和 (B) 分开了。

以 (mathtt{b}) 作为 (A) 来举例子。(mathtt{b}) 对应的节点是 5 号节点。我们可以发现，5 号节点的子树中长度大于 3 的子串还是可以作为 (B) 的。这个 3 是怎么来的呢？其实就是 5 号点的子树中次深的节点到 5 号节点的距离，即 4 号节点到 5 号点的距离。

具体一点，合法的情况有

A	B
(mathtt{b})	(mathtt{abba})
(mathtt{b})	(mathtt{abbaa})

当然，比如说 ((S,5)) 这条边有两个字母 (mathtt{ab})，那么 (A) 就可以是 (mathtt{a})，也可以是 (mathtt{ab}) 了。如果(A) 是 (mathtt{a})，那么只需要在每个 (B) 前添一个 (mathtt{b}) 即可。说简单一点，就是 (A) 和 (B) 可以不在同一条边中，而是在同一条边中断开，但是 (B) 一定要对应着最深节点除去次深节点的部分。那么这一条边又可以贡献 (len imes(mathbb{maxdep}-mathbb{secdep}))。

三、代码：

#include <iostream> // 由于我的代码使用后缀自动机来建后缀树，所以可能会有不分叉的节点，因此特判会多一些。
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long LL;
#define FILEIN(s) freopen(s, "r", stdin)
#define FILEOUT(s) freopen(s, "w", stdout)
#define mem(s, v) memset(s, v, sizeof s)

inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int MAXN = 400005;
const int INF = 1e8;

int n, tot = 1, las = 1;
LL ans;
int maxd[MAXN], sec[MAXN], head[MAXN], idx;
int dep[MAXN];
char ch[MAXN];

struct Node {
    int ch[27];
    int fa, maxlen;
}node[MAXN << 1];

struct Edge {
    int y, next;
    Edge() {}
    Edge(int _y, int _next) : y(_y), next(_next) {}
}e[MAXN << 1];

inline void connect(int x, int y) {
    e[++idx] = Edge(y, head[x]);
    head[x] = idx;
}

void extend(int c) {
    int z = ++tot, v = las; las = tot;
    node[z].maxlen = node[v].maxlen + 1;
    for (; v && node[v].ch[c] == 0; v = node[v].fa) node[v].ch[c] = z;
    if (!v) node[z].fa = 1;
    else {
        int x = node[v].ch[c];
        if (node[x].maxlen == node[v].maxlen + 1) node[z].fa = x;
        else {
            int y = ++tot;
            node[y] = node[x];
            node[y].maxlen = node[v].maxlen + 1;
            node[x].fa = node[z].fa = y;
            for (; v && node[v].ch[c] == x; v = node[v].fa) node[v].ch[c] = y;
        }
    }
}

void dfs1(int x) {
    int len = node[x].maxlen - node[node[x].fa].maxlen;
    dep[x] = dep[node[x].fa] + len;
    ans += 1LL * len * (len - 1) / 2;
    for (int i = head[x]; i; i = e[i].next) {
        int y = e[i].y;
        dfs1(y);
    }
}

void dfs2(int x) {
    if (head[x]) maxd[x] = -INF;
    sec[x] = -INF;
    for (int i = head[x]; i; i = e[i].next) {
        int y = e[i].y;
        dfs2(y);
        // maxd[x] = max(maxd[x], maxd[y] + node[y].maxlen - node[x].maxlen);
        int len = node[y].maxlen - node[x].maxlen;
        if (maxd[y] + len > maxd[x]) {
            sec[x] = maxd[x];
            maxd[x] = maxd[y] + len;
        }
        else sec[x] = max(sec[x], maxd[y] + len);

        sec[x] = max(sec[x], sec[y] + len);
    }
    int len = node[x].maxlen - node[node[x].fa].maxlen;
    ans += 1LL * len * (maxd[x] - max(0, sec[x]));
}

int main() {
    //FILEIN("in.txt");
    n = read();
    scanf("%s", ch + 1);
    reverse(ch + 1, ch + n + 1);
    for (int i = 1; i <= n; ++i) {
        extend(ch[i] - 'a' + 1);
    }
    for (int i = 2; i <= tot; ++i) {
        connect(node[i].fa, i);
    }
    dfs1(1);
    dfs2(1);
    printf("%lld
", ans);
    return 0;
}