前情提要:
通俗地说决策树算法(一)基础概念介绍
一. 概述
上一节,我们介绍了决策树的一些基本概念,包括树的基本知识以及信息熵的相关内容,那么这次,我们就通过一个例子,来具体展示决策树的工作原理,以及信息熵在其中承担的角色。
有一点得先说一下,决策树在优化过程中,有3个经典的算法,分别是ID3,C4.5,和CART。后面的算法都是基于前面算法的一些不足进行改进的,我们这次就先讲ID3算法,后面会再说说它的不足与改进。
二. 一个例子
众所周知,早上要不要赖床是一个很深刻的问题。它取决于多个变量,下面就让我们看看小明的赖床习惯吧。
| 季节 | 时间已过 8 点 | 风力情况 | 要不要赖床 |
|---|---|---|---|
| spring | no | breeze | yes |
| winter | no | no wind | yes |
| autumn | yes | breeze | yes |
| winter | no | no wind | yes |
| summer | no | breeze | yes |
| winter | yes | breeze | yes |
| winter | no | gale | yes |
| winter | no | no wind | yes |
| spring | yes | no wind | no |
| summer | yes | gale | no |
| summer | no | gale | no |
| autumn | yes | breeze | no |
OK,我们随机抽了一年中14天小明的赖床情况。现在我们可以根据这些数据来构建一颗决策树。
可以发现,数据中有三个属性会影响到最终的结果,分别是,季节,时间是否过8点,风力情况。
要构建一颗决策树,首先我们要找到它的根,按照上一节所说,我们需要计算每一个属性的信息熵。
在计算每一个属性的信息熵之前,我们需要先根据历史数据,计算没有任何属性影响下的赖床信息熵。从数据我们可以知道,14天中,有赖床为8天,不赖床为6天。则
p(赖床) = 8 / 12.
p(不赖床) = 6 / 12.
信息熵为
H(赖床) = -(p(赖床) * log(p(赖床)) + p(不赖床) * log(p(不赖床))) = 0.89
接下来就可以来计算每个属性的信息熵了,这里有三个属性,即季节,是否过早上8点,风力情况,我们需要计算三个属性的每个属性在不同情况下,赖床和不赖床的概率,以及熵值。
说得有点绕,我们先以风力情况这一属性来计算它的信息熵是多少,风力情况有三种,我们分别计算三种情况下的熵值。
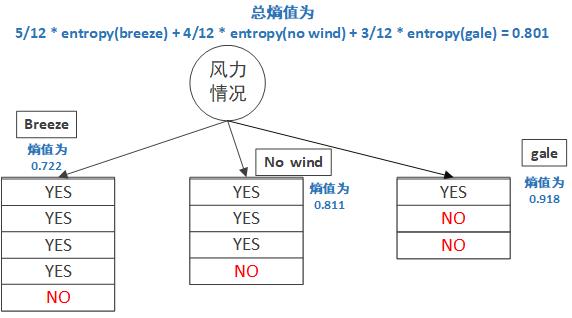
风力情况为 breeze 时,有 4 / 5 的概率会赖床,而 1 / 5 的概率不会赖床,它的熵为 entropy(breeze) = -(p(breeze,赖床) * log(p(breeze,赖床)) + p(breeze,不赖床) * log(p(breeze,不赖床))) 0.722。
风力情况为 no wind 时,和上面一样的计算,熵值为 entropy(no wind) = 0.811
风力情况为 gale 时,熵值为 entropy(gale) = 0.918
最终,风力情况这一属性的熵值为其对应各个值的熵值乘以这些值对应频率。
H(风力情况) = 5/12 * entropy(breeze) + 4/12 * entropy(no wind) + 3/12 * entropy(gale) = 0.801
还记得吗,一开始什么属性没有,赖床的熵是H(赖床)=0.89。现在加入风力情况这一属性后,赖床的熵下降到了0.801。这说明信息变得更加清晰,我们的分类效果越来越好。
以同样的计算方式,我们可以求出另外两个属性的信息熵:
H(季节) = 0.56
H(是否过 8 点) = 0.748
通过它们的信息熵,我们可以计算出每个属性的信息增益。没错,这里又出现一个新名词,信息增益。不过它不难理解,信息增益就是拿上一步的信息熵(这里就是最原始赖床情况的信息熵)减去选定属性的信息熵,即
信息增益 g(季节) = H(赖床) - H(季节) = 0.33
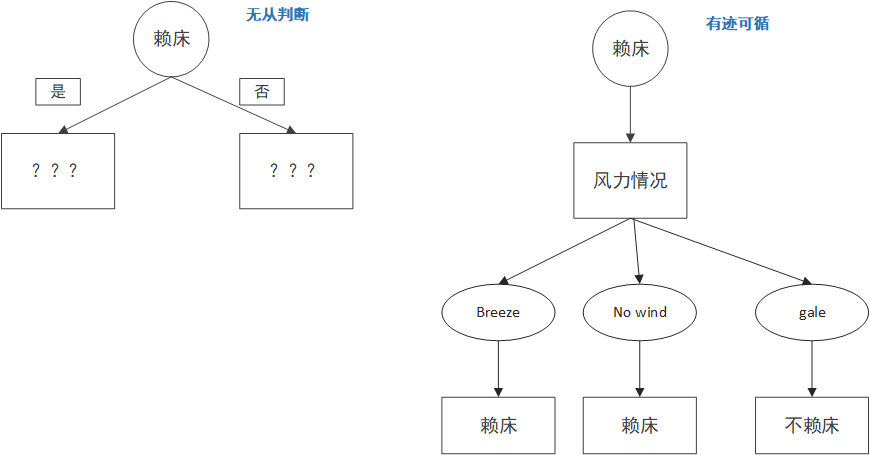
这样我们就能计算每个属性的信息增益,然后选取信息增益最大的那个作为根节点就行了,在这个例子中,很明显,信息增益最大的是季节这个属性。
选完根节点怎么办?把每个节点当作一颗新的树,挑选剩下的属性,重复上面的步骤就可以啦。
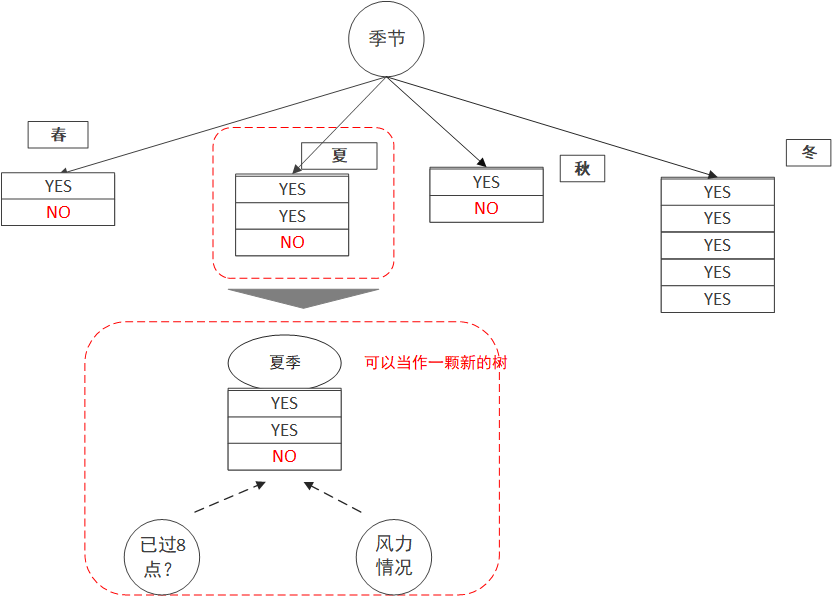
当全部都遍历完之后,一颗完整的树也就构建出来了,这个例子中,我们最终构造的树会是这个样子的:
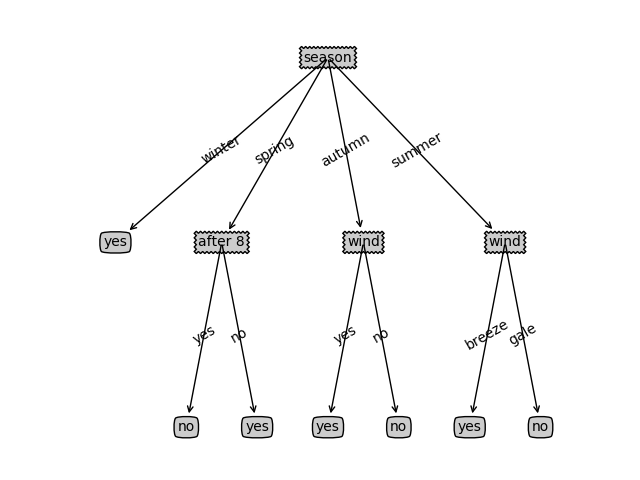
三. 过拟合与剪枝
在构建决策树的时候,我们的期望是构建一颗最矮的决策树,为什么需要构建最矮呢?这是因为我们要避免过拟合的情况。
什么是过拟合呢,下图是一个分类问题的小例子,左边是正常的分类结果,右边是过拟合的分类结果。
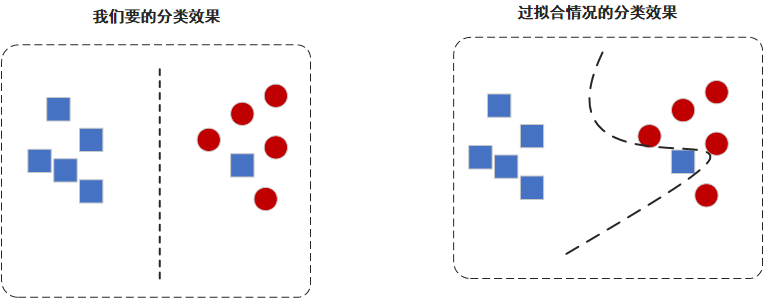
在现实世界中,我们的数据通常不会很完美,数据集里面可能会有一些错误的数据,或是一些比较奇葩的数据。如上图中的蓝色方块,正常情况下我们是允许一定的误差,追求的是普适性,就是要适应大多数情况。但过拟合的时候,会过度追求正确性,导致普适性很差。
剪枝,即减少树的高度就是为了解决过拟合,你想想看,过拟合的情况下,决策树是能够对给定样本中的每一个属性有一个精准的分类的,但太过精准就会导致上面图中的那种情况,丧失了普适性。
而剪枝又分两种方法,预剪枝干,和后剪枝。这两种方法其实还是蛮好理解的,一种是自顶向下,一种是自底向上。我们分别来看看。
预剪枝
预剪枝其实你可以想象成是一种自顶向下的方法。在构建过程中,我们会设定一个高度,当达构建的树达到那个高度的时候呢,我们就停止建立决策树,这就是预剪枝的基本原理。
后剪枝
后剪枝呢,其实就是一种自底向上的方法。它会先任由决策树构建完成,构建完成后呢,就会从底部开始,判断哪些枝干是应该剪掉的。
注意到预剪枝和后剪枝的最大区别没有,预剪枝是提前停止,而后剪枝是让决策树构建完成的,所以从性能上说,预剪枝是会更块一些,后剪枝呢则可以更加精确。
ID3决策树算法的不足与改进
ID3决策树不足
用ID3算法来构建决策树固然比较简单,但这个算法却有一个问题,ID3构建的决策树会偏袒取值较多的属性。为什么会有这种现象呢?还是举上面的例子,假如我们加入了一个属性,日期。一年有365天,如果我们真的以这个属性作为划分依据的话,那么每一天会不会赖床的结果就会很清晰,因为每一天的样本很少,会显得一目了然。这样一来信息增益会很大,但会出现上面说的过拟合情况,你觉得这种情况可以泛化到其他情况吗?显然是不行的!
C4.5决策树
针对ID3决策树的这个问题,提出了另一种算法C4.5构建决策树。
C4.5决策树中引入了一个新的概念,之前不是用信息增益来选哪个属性来作为枝干嘛,现在我们用增益率来选!

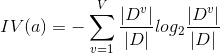
这里面,IV(a)这个,当属性可选的值越多(比如一年可取365个日期)的时候,它的值越大。
而IV(a)值越大,增益率显然更小,这就出现新问题了。C4.5决策树跟ID3决策树反过来,它更偏袒属性可选值少的属性。这就很麻烦了,那么有没有一种更加公正客观的决策树算法呢?有的!!
CART 决策树
上面说到,ID3决策树用信息增益作为属性选取,C4.5用增益率作为属性选取。但它们都有各自的缺陷,所以最终提出了CART,目前sklearn中用到的决策树算法也是CART。CART决策树用的是另一个东西作为属性选取的标准,那就是基尼系数。
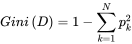
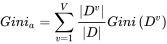
第一条公式中pk表示的是每个属性的可选值,将这些可选值计算后累加。这条公式和信息增益的结果其实是类似的,当属性分布越平均,也就是信息越模糊的时候,基尼系数值会更大,反之则更小。但这种计算方法,每次都只用二分分类的方式进行计算。比如说上面例子中的季节属性,有春夏秋冬四个可选值(春,夏,秋,冬)。那么计算春季的时候就会按二分的方式计算(春,(夏,秋,冬))。而后面其他步骤与ID3类似。通过这种计算,可以较好得规避ID3决策树的缺陷。
所以如果用CART算法训练出来的决策树,会和我们上面ID3训练出来的决策树有些不一样。在下一篇文章就会用sklearn来使用CART算法训练一颗决策树,并且会将结果通过画图的方式展现。
推荐阅读:
Scala 函数式编程指南(一) 函数式思想介绍
Actor并发编程模型浅析
大数据存储的进化史 --从 RAID 到 Hadoop Hdfs
C,java,Python,这些名字背后的江湖!