算法之狄克斯特拉算法 --《图解算法》

2019你好！好好生活，好好工作！

狄克斯特拉算法

狄克斯特拉算法(Dijkstra )用于计算出不存在非负权重的情况下，起点到各个节点的最短距离

可用于解决2类问题：

从A出发是否存在到达B的路径；
从A出发到达B的最短路径(时间最少、或者路径最少等)，事实上最后计算完成后，已经得到了A到各个节点的最短路径了；
其思路为：

(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。

(2) 更新该节点对应的邻居节点的开销，其含义将稍后介绍。

(3) 重复这个过程，直到对图中的每个节点都这样做了。

(4) 计算最终路径。

我们根据书中的例子给出相关的具体实现

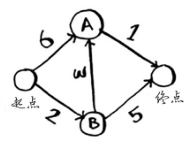
因为个人最经常使用的是OC语言，所以先用OC简单实现了一下，有不对之处还请告知，谢谢！

- (void)installDijkstra
{
    //用来记录已经被便利过该节点所有邻居的节点
    NSMutableArray *processed= [NSMutableArray array];
   //描述图的
    NSMutableDictionary *origianldic = [NSMutableDictionary dictionary];
    [origianldic setObject:@{@"a":@6,@"b":@2} forKey:@"start"];
    [origianldic setObject:@{@"fin":@1} forKey:@"a"];
    [origianldic setObject:@{@"a":@3,@"fin":@5} forKey:@"b"];
    //创建开销
    NSMutableDictionary *costDic = [NSMutableDictionary dictionary];
    costDic[@"a"] = @6;
    costDic[@"b"] = @2;
    costDic[@"fin"] = @(NSIntegerMax);
    //记录该节点的父节点的
    NSMutableDictionary *parentDic = [NSMutableDictionary dictionary];
    parentDic[@"a"] = @"start";
    parentDic[@"b"] = @"start";
    parentDic[@"fin"] = @"";
    
    NSString *node = [self findLowerCostNode:costDic array:processed];
    while (![node isEqualToString:@""]) {
        NSDictionary *tempDic = origianldic[node];
        for (NSString *key in tempDic.allKeys) {
            NSInteger newCount = [costDic[node]integerValue] + [tempDic[key]integerValue];
            if ([costDic[key] integerValue] > newCount) {
                costDic[key] = @(newCount);
                parentDic[key] = node;
            }
        }
        [processed addObject:node];
        node = [self findLowerCostNode:costDic array:processed];
    }
    NSLog(@"origianldic = %@,
costDic = %@,
parentDic = %@,
 processed = %@,
 NSIntegerMax = %ld",origianldic,costDic,parentDic,processed,NSIntegerMax);
    NSLog(@"--end --costDic = %@",costDic);
    NSLog(@"--end --parentDic = %@",parentDic);
}

/**
 找到开销最小的节点

 @param dic dic
 @param processArray 记录节点
 @return 为空说明已经查找完毕
 */
- (NSString *)findLowerCostNode:(NSDictionary *)dic array:(NSMutableArray *)processArray
{
    NSInteger lowerCost = [dic[@"fin"]integerValue];
    NSString *lowedNode = @"";
    for (NSString *key in dic.allKeys) {
        NSInteger costNum = [dic[key]integerValue];
        if (costNum < lowerCost && (![processArray containsObject:key]) ) {
            lowerCost = costNum;
            lowedNode = key;

        }
        
    }
    return lowedNode;
}

2019-01-13 21:24:14.382432+0800 HaiFeiTestProject[29763:1130947] --end --costDic = {
    a = 5;
    b = 2;
    fin = 6;
}

python实现

infinity = float('inf')
graph = {'start': {'a': 6, 'b': 2}, 'a': {'fin': 1}, 'b': {'a': 3, 'fin': 5}, 'fin': {}}
costs = {'a': 6, 'b': 2, 'fin': infinity}
parents = {'a': 'start', 'b': 'start', 'fin': None}
processed = []

def main(graph, costs, parents, processed, infinity):
    node = find_lowest_cost_node(costs, processed)
    while node is not None:
        for n in graph[node].keys():
            new_cost = costs[node] + graph[node][n]
            if costs[n] > new_cost:
                costs[n] = new_cost
                parents[n] = node
        processed.append(node)
        node = find_lowest_cost_node(costs, processed)


def find_lowest_cost_node(costs, processed):
    lowest_cost = float('inf')
    lowest_cost_node = None
    for node in costs:
        if lowest_cost > costs[node] and node not in processed:
            lowest_cost = costs[node]
            lowest_cost_node = node
    return lowest_cost_node


main(graph, costs, parents, processed, infinity)
print(costs)
print(parents)

运行结果

算法图解之狄克斯特拉算法 和书中描述基本一致，可参考！